§ 6. n-мерное евклидово пространство.
Скалярное произведение

6.1. n-мерное пространство. Множество всевозможных систем (x₁, ..., х_п) действительных (комплексных) чисел называется n-мерным действительным (комплексным) пространством и обозначается через R_n. Каждую систему мы будем обозначать одной (жирной) буквой без индекса:

х - ( x₁, ..., х_п)

59

и называть точкой или вектором R_n (пространства R_n). Числа x ₁ ..., х_п называют координатами точки (вектора) х или еще компонентами вектора х.

Две точки

х = (x_l..... х_п), х ' = (х'₁, ..., х' _п)

считаются равными, если их соответствующие координаты равны

х_j = х' _j (j = 1,..., n).

В других случаях х и х ' различны ( х ≠ х').

Системы (векторы) х - (x₁, ..., х_п), _у = (y₁ ..., у_п) можно складывать, вычитать и умножать на числа α, β, ... -действительные, если R_n есть действительное пространство, и комплексные, ели R_n - комплексное пространство¹.

По определению суммой векторов хну называется вектор

х + у = (x_l + у₁, х₂, + у₂, ..., х_n + у_п), (1)

а разностью - вектор

х - у = (x₁ - у₁, .... х_п - у_п). (2)

Произведением же числа α на вектор х или вектора х на число α называется вектор

α х = хα = (αx₁, ..., αх_п).

Наконец, вектор -х определяется равенством

-х = (-1) x = (-x₁, -х₂, .... -х_п).

Вводится еще понятие нулевого вектора, компоненты которого равны нулю: 0 = (0, ..., 0). Очевидно, выполняются свойства:

• 1) х + у = у + х,
• 2) ( х + у) + z = х + ( у + z) ,

60

• 3) х - у = х + (-l) y,
• 4) α х + αy = α( х + у ),
• 5) α x + β x) = (α + β) х,
• 6) α(β x) = (αβ) x ,
• 7) 1 ∙ x = х,
• 8) х + (- х) = 0,

где α, β - числа, а x, у ∈ R_л.

Пространство R_n называется линейным пространством, потому что для него выполняются перечисленные выше свойства 1) - 8), см. ниже замечание 1.

Число (неотрицательное)

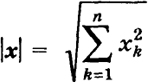(3)

называется длиной или нормой вектора х - (x₁, ..., х_п) в действительном пространстве R_n.

Расстояние между точками x = (x₁ ..., х_п) и у = (y₁,..., y_n) действительного пространства R_n определяется по формуле

(4)

6.2. Скалярное произведение в действительном пространстве R_n. Скалярным произведением двух векторов х = (x₁ ..., х_п) и у = (у₁, ..., у_п) в действительном пространстве R_n (числа x ₁, y₁ действительные) называется число

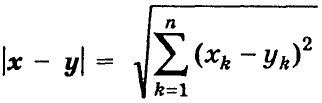(5)

Скалярное произведение в действительном пространстве R_n обладает свойствами:

61

• а) ( х, х) ≥ 0; при этом равенство нулю имеет место тогда и только тогда, когда х = 0 = (0, .... 0),
• б) (х, у) = (у, х),
• в) (α х + βy, z) = α( x, z) + β( y, z).

В самом деле.

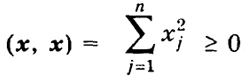
и равенство может быть лишь, если x _j = ... = х_п = 0. Далее,

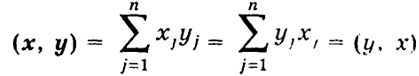
и

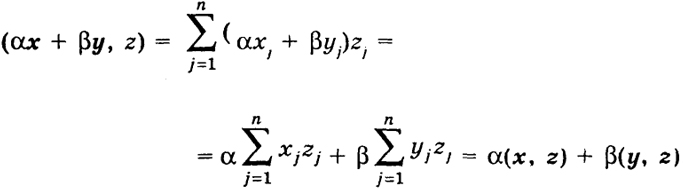
6.3. Скалярное произведение в комплексном пространстве R_n. Скалярным произведением двух векторов х = (x₁, ..., х_п) и у - (y₁ ..., у_п) в комплексном пространстве R_n называется число

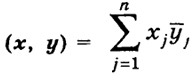(5')

где у _j есть комплексное число, сопряженное к числу y_j (по определению, если z = α + β i, где α и β действительные, то z = α - β i).

Скалярное произведение в комплексном пространстве обладает свойствами:

62

• а') ( х, х) ≥ 0; при этом равенство нулю имеет место тогда и только тогда, когда х = 0 = (0, ..., 0),
• б') ( х,у) = ( у, х),
• в') (α x + β у, z) = α( x, z) + β( у, z).

В самом деле,

и равенство может быть, лишь если x_j - ... - х_п = 0. Далее,

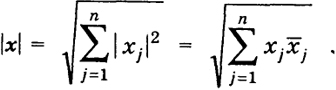
Здесь мы воспользовались свойствами операции сопряжения

z + z₁= z + z ₁ и zz₁ = z ∙ z ₁ .Наконец,

В комплексном пространстве R_n длина вектора х определяется при помощи равенства

(3')

а расстояние между точками х = (x₁, ..., х_п) и у = (y₁, ..., у_п)

(4')

Легко видеть, что при действительных х., у. выражения (3)

63

и (4) являются частными случаями выражений (3'), (4').

Пространство R_n (действительное или комплексное), в котором введено понятие скалярного произведения по формуле (5) (соответственно (5')), называется евклидовым n-мерным пространством.

6.4. Неравенства Буняковского. Для скалярного произведения в действительном и комплексном пространстве справедливо неравенство (Буняковского¹)

|(x, y)| ≤ √( x,x) √( y,y) . (6)

Докажем его только в действительном случае. В самом деле, для любого действительного числа А.

0 ≤ ( x + λy, х + λ у) =( х, х) + λ( y, х) + λ( х, у) + λ( y, у) =
= ( х, х) + 2( х, у)λ + ( у, у)λ² = а + 2bλ + сλ²,

где а = ( х, х), b = ( х, у), с = ( у, у). Мы видим, что квадратный многочлен

а + 2bλ + сλ² ≥ 0 (-∞ < λ < ∞)

неотрицателен для любого действительного λ. Поэтому весь его график лежит выше оси λ, а это может быть, только если дискриминант многочлена отрицателен или равен нулю, т. е. если b² - ас ≤ 0 или b² ≤ ас, и мы получили неравенство Буняковского (6).

На языке компонент векторов х и у неравенство (6) можно записать так:

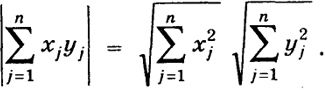(7)

64

Таким образом, каковы бы ни были действительные числа х_j, у_j, выполняется неравенство (7).

В силу (3) неравенство Буняковского можно написать так:

|(x, y)| ≤ | x || y |.

Но тогда существует и притом единственное число λ, удовлетворяющее неравенствам -1 ≤ λ ≤ 1, для которого имеет место точное равенство

( x, у) = λ| x || y |.

Отметим, что на [0, π] функция cos t имеет однозначную строго убывающую обратную функцию, с областью значений на [-1, 1]. Поэтому для каждого λ (-1 ≤ λ ≤ 1) существует единственный угол ω (0 ≤ ω ≤ π) такой, что λ = cos ω. Таким образом, мы доказали равенство

( х, у) = | x|| y|cos ω. (8)

Число со называется углом между n-мерными векторами х и у, хотя на самом деле при п > 3 векторы х и у являются вовсе не реальными отрезками, а математическими абстракциями.

Векторы х и у называются ортогональными, если скалярное их произведение равно нулю

Из (8) следует, что для того, чтобы ненулевые векторы х и у были ортогональными, необходимо и достаточно, чтобы угол между ними ω = π/2.

6.5. Неравенство Минковского. Отметим важное неравенство (Минковского¹)

| х+ у| ≤ | x| + | у |, (9)

65

или на языке компонент

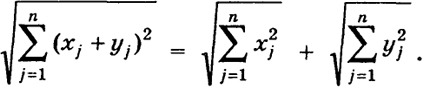(10)

Его можно доказать так:

| х + у |² = ( х + у, х + у) = ( х, х) + 2( x, у) + ( у, у).

Используя неравенство Буняковского (6), имеем

| х + у²| ≤ ( х, х) + 2√( x,x) √( y,y) + ( y, y) = (√( x, x)+√( y, y))²,

откуда следует (9). Из (9) следует неравенство

| x | - | y | ≤ | x - у |, (11)

потому что

| x | - | х - у + у| ≤ | х - у | + | у |,
| у| = | у - х+ х| ≤| х - у| + | x |

Задача. Найти угол между векторами (1, 0, 1, 0), (1, 1, 1, 1).

Замечание 1. Произвольное множество Е, состоящее из элементов х, у, z, ... любой природы, называется линейным пространством, если существует закон, в силу которого для любых двух элементов x, у ∈ Е определены элементы х+у ∈ Е и х - у ∈ Е, называемые соответственно суммой, разностью х и у, и для любого действительного или комплексного числа а и элемента х ∈ Е определен элемент αх - хα. ∈ Е, называемый произведением α на х или х на α, так что выполняются перечисленные выше в этом параграфе свойства 1) - 8), где - х = (-1) x, и 0 = 0 х, ∀ x ∈ Е.

R_n можно рассматривать как пример линейного пространства, но существуют и другие интересные примеры. Например, совокупность С непрерывных на отрезке [ а, b] функций f, φ, ψ, ..., если считать, что f + φ, f - φ, α f определены соответственно как f( x) + φ( x), f( x) - φ( x), αf( x), есть линейное пространство.

66

Линейное пространство с умножением его элементов на действительные (комплексные) числа называется действительным (комплексным) линейным пространством.

Замечание 2. Если в каком-либо линейном пространстве Е каждым двум его элементам х, у приведено в соответствие число ( х, у), удовлетворяющее сформулированным выше свойствам а), б), в) в действительном случае и а'), б'), в') в комплексном случае, то говорят, что в Е введено скалярное произведение.

Выше было дано определение k-мерного евклидова пространства - это пространство Ля, в котором определено скалярное произведение по формулам соответственно (5) или (5').

67

---