5.1. Понятие вектора. В этом параграфе мы будем рассматривать реальное пространство. Понятие вектора в реальном пространстве читателю известно из элементарной геометрии.
Вектором (в реальном пространстве) называется направленный отрезок АВ→ с начальной точкой А и конечной
48
точкой В, который можно передвигать параллельно самому себе. Таким образом, считается, что два направленных отрезка АВ→ и А1В1→ , имеющие равные длины (|АВ| = |A1B1|) и одно и то же направление, определяют один и тот же вектор α, и в этом смысле пишут α = АВ→ = А1В1→ (рис. 2).
Длиной |АВ→| = |α| вектора АВ→ = аα называется число (неотрицательное), равное длине отрезка АВ, соединяющего точки А и В. Будем также писать |АВ→| = |АВ|.
Векторы, лежащие на одной прямой или на параллельных прямых, называются коллинеарными. Если точки А и В совпадают, то
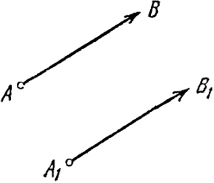
Рис. 2
АВ→ = АА→ = 0 считают тоже вектором - нулевым вектором. Его длина равна нулю (|0| = 0), а направление для него не имеет смысла.
В геометрии рассматривают сложение и вычитание векторов и умножение их на действительные числа. По определению произведение аа = аа вектора а на число а или числа а на вектор а есть вектор, длина которого равна |α a | = |α| ∙ | а |, а направление совпадает с а, если а > 0, или противоположно а, если α < 0. При α = 0 длина |α а | равна нулю и вектор α а превращается в нулевой вектор (точку), не имеющий направления.
Вектор е называется единичным, если его длина равна 1, т. е. | е | = 1. Если b = α е и е - единичный вектор, то | b | = = |α|, потому что
| b | = |α| ∙ | e | = |α| ∙ 1 = |α|
49
По определению векторы а, b, с, ...,взятые в конечном числе, складываются по правилу замыкания цепочки этих
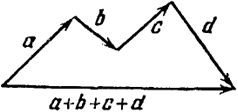
Рис. 3
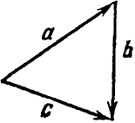
Рис. 4
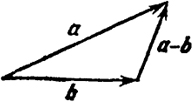
Рис. 5
векторов. Рис. 3 и 4 напоминают нам, как это делается. На рис. 5 показано, кроме того, как вычитаются векторы.
5.2. Проекция вектора. Проекцией точки А на прямую L (рис. 6) называется точка А', в которой
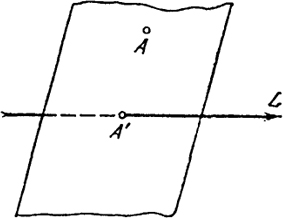
Рис. 6
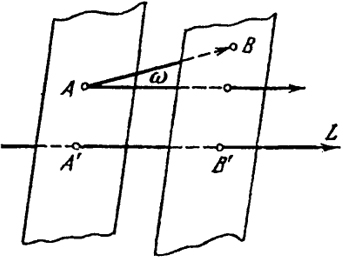
Рис. 7
пересекаются прямая L с плоскостью, перпендикулярной к L, проходящей через точку А.
Зададим направленную прямую L (рис. 7) и вектор а = АВ→. Проекцией вектора а = АВ→ на направленную прямую L называется вектор А'В'→, где А', В' - соответственно проекции точек А, В на L (см. рис. 7).
50
Проекцию вектора а на направленную прямую L будем обозначать символом npL→a.
При данной направленной прямой L проекции А'В'→ любых векторов АВ→ на L лежат в L и направлены, как L, либо - в противоположную сторону.
Впрочем, если вектор АВ→ нулевой или перпендикулярен к L, то его проекция на L есть, очевидно, нулевой вектор, не имеющий направления.
Наряду с проекцией вектора а на направленную прямую L, которая представляет собой вектор, введем еще новое понятие - числовую проекцию вектора а на направленную прямую L. Это есть число, обозначаемое нами символом npL a (без стрелки) и определяемое следующим образом.
Числовой проекцией вектора а = АВ→ на направленную прямую L называется произведение длины вектора а = АВ→ на косинус угла со между вектором а и направлением L:
npL a = | a |cos( a, L) = | a |cos ω (0 ≤ ω ≤ π).
Отметим следующие случаи: если a = 0 или если ω =
то np
L a = 0; если
а ≠ 0 и 0 ≤ ω ≤
, то числовая проекция положительна (np
L a > 0) и равна, очевидно, длине вектора
А'В'→: np
L a = |
АВ|cos ω = |
А'В'|; при этом сам вектор
А'В'→ направлен так же, как
L; если же
а ≠ 0 и
< ω ≤ π, то числовая проекция отрицательна (np
L a < 0) и равна, очевидно, длине вектора
А'В'→, взятой со знаком минус:
51
прL→ = |AB→|COS ω = -|А'В'→| = -|A'B'|,
при этом сам вектор А'В'→ направлен в сторону, противоположную L.
Справедливо очевидное равенство, выражающее связь между проекцией вектора а на направление L и его числовой проекцией на L:
npL→ a = enpL a.
Здесь е - единичный вектор, направленный, как L.
Если векторы а и b лежат на направленной прямой L, то их можно записать в виде
а = α е, b = епр L a,
где е - единичный вектор, направленный так же, как L, а α и β - числа. Эти числа могут быть положительными, отрицательными или нулем.
Справедливы очевидные равенства
α е ±β e = (α ± β) е, (1)
показывающие, что сложение и вычитание указанных векторов сводится к сложению или вычитанию соответствующих чисел α, β р.
5.3. Свойства проекций векторов. Числовые проекции векторов а, b на данное направление L обладают следующими свойствами:
npL a + npL b = npL(a + 6), (2)
прL (α а) = αпpL a. (3)
Свойство (2) усматривается на рис. 8:
npL→ a + npL→ b = А'В'→ + В'С'→ = А'С'→ = npLc = npL ( a + b).
52
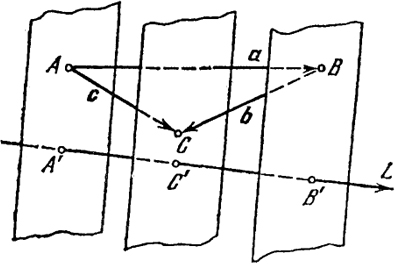
Рис. 8
Но тогда
eпp L a + епр L b = enp L ( a + b),
откуда следует (2) (см. (1)).
Так как а = ( а - b) + b (см. рис. 5), то
np L ( a - b) + npLb = np L a,
и, следовательно,
np L a - npL b = np L (a - b). (2')
Докажем (3). Считая, что угол между вектором а и направлением L равен 0), имеем
при a > 0:
np L (α a) = |α a|cos ω = α| a |cos ω = αnp L a;
при α < 0:
np L (α a) = |α a|cos (π - ω) = α| a|cos ω = αпр L a
Ведь при а < 0 вектор α а направлен в сторону, противоположную направлению а, и если а образует с L угол ω, то α a образует с L угол π - ω.
При α = 0 левая и правая части (3) обращаются в нуль.
53
5.4. Скалярное произведение векторов. Назовем скалярным произведением двух векторов а и b число(а, b), равное произведению длин этих векторов, помноженному на косинус угла со между ними:
аb = ( а, b) = | a || b |cos( a, b) = | a || b |cos ω. (4)
Очевидно, можно еще сказать, что скалярное произведение векторов а и b есть произведение длины вектора |b| на числовую проекцию вектора а на направление b или произведение длины | а| на числовую проекцию b на направление а:
аb = ( а, b) = | а |пр a b = | b |прb a.
Скалярное произведение обладает свойствами:
( а, b) = ( b, а), (5)
( а, b + с) = ( а, b) + ( а, с), (6)
( а, α b) = α( а, b). (7)
Равенство (5) непосредственно вытекает из определения скалярного произведения. Равенство (6) доказывается так:
( а, b + с) = | а |пр а ( b + с) = | а |пра b + | а |пр а с = ( а, b) + ( а, с).
Равенство (7) доказывается следующим образом:
( а, α b) = | а |пр а (α b) = | а |αпр а b = α( а, b).
Из (6) и (7), учитывая, (5), следует
( а + b, с) = ( а, с) + ( b, с), (6')
(α а, b) = α( a, b). (7')
Пример (из физики). Если тело под действием силы а передвинулось прямолинейно вдоль вектора b, то работа W, выполненная силой a как известно из физики, равна
54
произведению величины силы | а | на путь FDIV/b | и еще на косинус угла между векторами а и b
W = | а| |b|cos( a, b).
Но тогда
W = (а,b),
т. е. указанная работа равна скалярному произведению векторов а и b.
5.5. Прямоугольная система координат. Теперь мы переходим к аналитическому описанию векторов и точек пространства - при помощи чисел. Введем в пространстве прямоугольную систему координат х, у, z, т. е. три взаимно перпендикулярные направленные прямые, проходящие через некоторую точку О, называемые осями координат х, у, z (рис. 9). Предполагается, что для данной системы координат выбран единичный отрезок, при помощи которого измеряются все прочие отрезки. Точка О называется началом координат.
Зададим произвольную точку А трехмерного пространства. Направленный отрезок ОА→ называется радиус-вектором точки А. Радиус-вектор в свою очередь определяет вектор а ( а = ОА→), который можно переносить в пространстве параллельно самому себе. Числовые проекции радиус-вектора а на оси х, у, z обозначим соответственно х, у, z. Это координаты точки А; при этом координата х называется абсциссой, координата у - ординатой и координата z - аппликатой точки А.
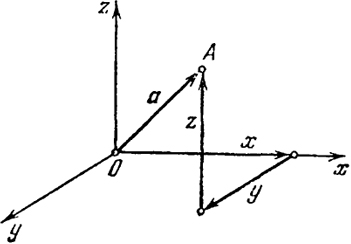
Рис. 9
55
Между точками А пространства и их радиус-векторами ОА→ или, что все равно, тройками чисел (х, у, z), являющимися координатами точки А или проекциями ОА на оси, имеется взаимно однозначное соответствие. В силу сказанного не будет путаницы, если мы будем называть тройку чисел (х, у, z) точкой А, имеющей эти числа своими координатами или радиус-вектором а, имеющим эти числа своими проекциями.
Мы будем писать а = (х, у, z) и говорить, что а или (х, у, z) есть вектор, равный радиус-вектору точки Аимеющему координаты х, у, z. Но, конечно, можно считать, что вектор а равен какому-либо другому направленному отрезку CD→, равному ОА→ (CD→ = ОА→), т.е. имеющему то же направление и ту же длину, что и ОА→. В этом случае проекции а на оси координат часто обозначают символами ах, ау, аz и пишут а =(ах, ау, аг).
Из определения вектора как направленного отрезка, который можно передвигать в пространстве параллельно самому себе, следует, что два вектора а = (x1, y1, z1) и b = = (х2, y2, z2) равны тогда и только тогда, если выполняются одновременно равенства: x1 = x2, y1 = y2, z1 = z2.
Справедливы равенства
(х, у, z) ± (х', у', г') = (х±х',у ± у', z ± z'), (8)
α(х, у, z) = (αx, αy, αz). (9)
Равенство (8) следует из того, что проекция суммы или разности векторов (на ось х или у или 0) равна сумме или разности проекций слагаемых.
Равенство же (9) следует из того, что проекция вектора оса (на ось х или у или z) равна произведению а на проекцию а.
Обозначим через i, j, k единичные (имеющие длину, равную 1) векторы, имеющие соответственно то же
56
направление, что и оси х, у, z. Векторы i, j, k называют ортами осей х, у, z. Произвольный вектор (х, у, z) может быть записан в виде
(х, у, z) = xi + yj + zk. (10)
В самом деле,
i = (1, 0, 0), j = (0, 1, 0), k = (0, 0, 1).
Поэтому в силу (8) и (9)
xi + yj + zk = x (1, 0, 0) + y (0, 1, 0) + z (0, 0, 1) = (х, 0, 0) + (0, у, 0) + (0, 0, z) = (х; у, z).
Отметим равенства, имеющие место для скалярных произведений ортов осей
ii = jj = kk = 1, ij = ik = jk = 0.
Пусть теперь а = (х, у, z) и b = ( x', y', z'). Тогда
ab = ( а, b) = xx ' + yy ' + zz'. (11)
В самом деле, на основании (6), (7), (6'), (7')
ab = (xi + yj + zk)(x' i + y' j + z' k) =
= xx' ii + xy' ij + xz' ik + yx' ji + yy' jj + yz' jk + zx' ki + zy' kj + zz' kk =
= xx' + yy' + zz'.
В частности, положив в этой формуле Ъ = а, получим, что
| а |2 = аа = х2 + у2 + z2,
откуда длина вектора а равна
| a | = + √x2 + y2 + z2.
Отсюда расстояние между точками а = (х, у, z) и b = ( x', y', z') равно (рис. 10)
| АВ | = | b - а | = +√(x'-x)2 +(y'-y)2 +(z'-z)2 .

Рис. 10
57
Для дальнейшего будет важно подвести итог сказанному. Для этого введем несколько иное наименование координат. Именно, введем в пространстве прямоугольную систему координат x1, х2, х3. В силу этого каждая точка пространства представлена тройкой чисел
x = ( x1, x2, x3).
Эту точку мы обозначили жирной буквой х и назвали также вектором х с компонентами х1, х2, х3.
Мы доказали, что сложение и вычитание векторов и умножение их на числа выражаются на языке троек (x1, х2, х3) следующим образом:
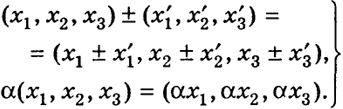 (12)
(12)
Скалярное произведение векторов х = (х1, х2, х3) и х ' = - (х'1, х'2, х'3) выражается через координаты векторов х и х' по формуле
хх ' = ( х, х') = x1x'1 + х2х'2 + х3х'3. (13)
Длина вектора х = (x1, x2, х3) есть неотрицательное число, равное
| x | = √x21+x22+x23. (14)
Наконец, расстояние между точками х = ( X1, x2, х3) и x ' = (х'1, х'2, х'3) равно
| x - x'| = √(x'1 - x1)2 + (x'2 - x2)2 + (x'3 - x3). (15)
Реальное пространство, геометрию которого мы здесь изучали, называется трехмерным пространством, потому что его точки естественным образом представляются тройками действительных чисел. Мы будем его обозначать через R3.
58
Произвольную плоскость естественно обозначить через R2. В R2 можно задать прямоугольную систему координат x1, х2, с помощью которой любую точку R2 или ее радиус-вектор можно представить парой чисел (x1, x2). Операции сложения и вычитания и умножения на число для векторов, принадлежащих к плоскости, очевидно, подчиняются выведенным нами условиям (12), где в скобках надо только всюду выбросить третьи компоненты. Скалярное произведение векторов, принадлежащих к нашей плоскости, тоже выражается формулой (13), где в правой части надо выбросить третий член. То же самое относится и к формулам (14) и (15).
Обобщением пространств R2 и R3 является пространство Rn, где п - произвольное натуральное число.
Пространство Rn при п > 3 является математической выдумкой. Впрочем, весьма гениальной выдумкой, которая помогает математически разбираться в сложных явлениях.
- Найти длину векторов (1, 1, 1), (1, -1, 1), (1, 2, 3).
- Найти угол между векторами (1, 0, 1), (1, 2, 3).
- Дан единичный куб (с длиной ребра, равной 1). Найти угол между выходящими из его вершины: а) главной диагональю и диагональю грани; б) между двумя диагоналями двух граней.
59
1Отметим, что в данной книге сначала излагается скалярное произведение векторов, затем аналитическая геометрия прямой и плоскости и после этого в §§ 11-13 излагаются понятия векторного и смешанного произведений векторов. При желании эти параграфы могут быть изложены непосредственно после § 6.
