§ 4. Система линейных уравнений. Теория Кронекера-Капелли¹

4.1. Система из п линейных уравнений с п неизвестными. Будем называть произвольную систему из п чисел (x₁ ..., х_п) n-мерным вектором и обозначать его также одной (жирной) буквой х:

x = (x₁, ..., Х_п).

Числа х_j (действительные или комплексные) называют компонентами вектора х. Вектор

0 = (0, ..., 0)

называется нулевым вектором.

Зададим систему из п линейных уравнений с п неизвестными

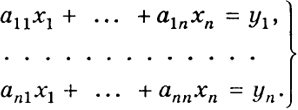(1)

Числа а_kl (действительные или комплексные), называемые коэффициентами системы (1), заданы. Будем еще говорить, что система (1) определяется матрицей

(2)

ее коэффициентов.

Нас будет интересовать вопрос о разрешимости системы (1) для каждого вектора (системы чисел)

Y = (y₁, ooo, У_n).

25

Система чисел (вектор)

X = (x₁ ..., Х_n)

называется решением системы уравнений (1), если числа х. удовлетворяют этим уравнениям.

4.2. Формулы Крамера.

Теорема 1. Если определитель системы (1) не равен, нулю:

Δ = |a_kl ≠ О,

то система (1) имеет единственное решение для любого вектора у, вычисляемое по формулам (Крамера¹)

х_j = Δ/Δ (j = 1, ..., n), (3)

где Δ ^j - определитель, получаемый из определителя Δ. если в нем заменить числа j-го столбца соответственно на числа у₁ ..., у_п:

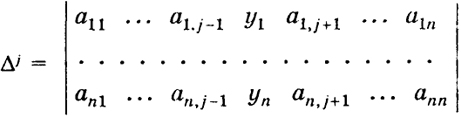(4)

Таким образом,

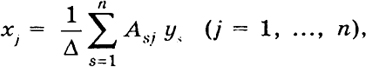(3')

где A_sj есть адъюнкт элемента a_sj в определителе Δ.

Доказательство. Пусть (х₁ ..., х_п) есть решение системы (1). Чтобы найти неизвестное число x₁ умножим первое уравнение системы (1) на адъюнкт А₁₁, второе - на А₂₁, ..., n-е - на A_n1 и сложим все уравнения системы. Тогда, учитывая, что

26

и

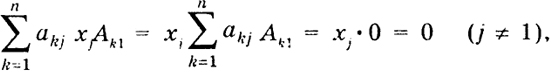
получаем x₁Δ = Δ¹, где

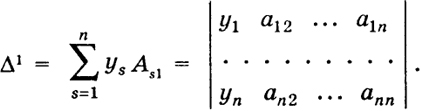
Следовательно, так как по условию Δ ≠ 0, то x₁ = Δ/Δ.

В общем случае при произвольном j умножаем первое уравнение системы (1) на А_1j , второе - на А_2j , ..., n-е - на А_пj, складываем эти уравнения и получаем на основании свойств определителей е), ж) равенство

т. е.

х₁ Δ = Δ _j ,

где

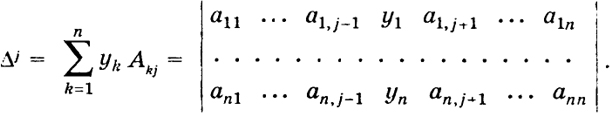
Отсюда в силу того, что Δ ≠ 0, следует равенство (3).

Мы доказали, что если (x₁, ..., х_п) есть решение системы (1), то числа х_j определяются формулами (3').

27

Обратно, совокупность чисел х_j - Δ'/Δ (j = 1, ..., п) является решением системы (1). В самом деле, подставляя X_j (j = 1, ..., п) в левую часть k -го уравнения (k = 1, ..., п) системы (1), на основании свойств е). ж) определителя, имеет

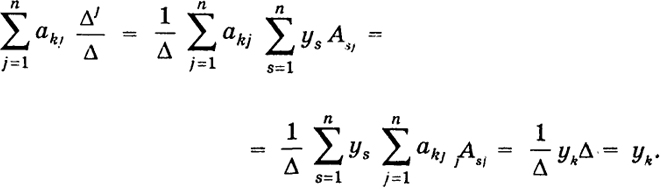
Таким образом, числа (3') действительно являются решением системы (1).

4.3. Однородная система. Система уравнений вида

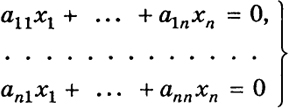(5)

называется однородной. Она является частным случаем системы (1) при y ₁ = ... = у_п = 0. Ясно, что нулевой вектор

x₁ = 0...,х_п = О

удовлетворяет однородной системе (5). Но может случиться, что однородная система (5) удовлетворяется не нулевым вектором х = (x₁ ..., х_п), т. е. вектором, имеющим хотя бы одну компоненту x_i ≠ 0. Его называют нетривиальным решением однородной системы (5), а нулевой вектор поэтому называют тривиальным решением однородной системы (5).

28

Теорема 2. Если определитель Δ однородной системы (5) не равен нулю (Δ ≠ 0), то эта система имеет только тривиальное решение.

В самом деле, в силу свойства г) все определители Δ' = 0 (см. (4)), поэтому в силу равенств (3) x_j = 0 (j = 1, ..., п).

Теорема 3. Если система уравнений (5) имеет нетривиальное решение, то ее определитель Δ необходимо равен нулю (Δ = 0).

В самом деле, если бы Δ ≠ 0, то по теореме 2 система (5) имела бы только одно тривиальное решение.

Выше мы исследовали линейную систему (1) в случае, когда ее определитель Δ ≠ 0. В этом случае было показано (теорема 1), что система (1) имеет для любой правой части у = (y₁, ..., у_п) единственное решение, вычисляемое по формулам (3).

4.4. Правило решения системы линейных уравнений. Теперь мы переходим к исследованию системы (1) в случае, когда ее определитель Δ = 0. Будем предполагать, что хотя бы один элемент матрицы А (см. (2)) не равен нулю и обозначим ранг А через k (k = = ранг А). Таким образом, 1 ≤ k < п.

Нашей целью будет доказать следующие правила (явным образом они сформулированы и доказаны Кронекером и Капелли).

Если мы хотим решить систему (1), для которой известно, что ранг матрицы А ее коэффициентов равен k, то мы должны узнать ранг расширенной матрицы

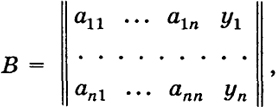
полученной присоединением к А столбца

29

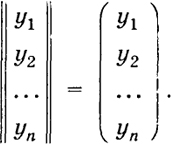
• 1) Если ранг В больше ранга А (ранг В > ранг А = k), то система (1) вовсе не имеет решений. Она противоречива - не существует вектора х = (x₁ ..., х_п), удовлетворяющего одновременно всем уравнениям (1).
• 2) Если ранг В равен рангу А (ранг В = ранг А = k), то система (1) имеет решения. Чтобы найти их, мы должны выбрать из системы (1) какие-нибудь k уравнений, матрица коэффициентов которых имеет ранг k, и решить эти k уравнений. Решений у этой системы из k уравнений будет бесконечно много, но их можно записать в обозримом виде.

При этом любое решение взятых нами k уравнений автоматически является решением остальных п - k уравнений системы (1).

Правила 1) и 2) исчерпывают возможные ситуации, потому что ранг В не может быть меньшим k.

Ведь матрица А по условию порождает не равный нулю определитель k-ro порядка, который порождается также и матрицей В.

4.5. Примеры приложения правил.

Пример 1. Система

имеет определитель

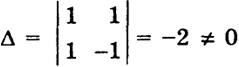
30

и потому имеет единственное решение, которое можно вычислить по формулам

х = Δ¹ /Δ, у = Δ² /Δ,

где

т. е.

Пример 2. Система

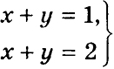(6)

имеет определитель, равный нулю. Матрица

имеет ранг А = 1. А матрица

имеет ранг В = 2. Так как ранг В > ранг А, то система (6) не имеет решений. Это видно, впрочем, и без нашей теории: одно и то же число не может равняться и 1 и 2.

Пример 3. Система

(7)

имеем определитель Δ = 0. Матрица

31

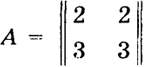
имеет ранг А = 1. Расширенная матрица

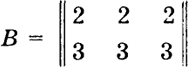
тоже имеет ранг В = 1. Так как ранг А = ранг В = 1, то берем одно уравнение

2х + 2 у = 2. (8)

Коэффициент при y не равен нулю, поэтому это уравнение можно решить относительно у:

У =

2 - 2 x

2

  = 1 - x. (9)

Формула (9) дает все решения уравнения (8). Мы можем задать любое значение х (- ∞ < х < ∞) и вычислить значение y по формуле (9). Получим систему (вектор) (х, y), удовлетворяющую уравнению (8). Множество всех систем (х, 1 - х), где х ∈ (-∞∞, со), образует множество всех решений уравнения (8). Эти решения автоматически являются решениями и второго уравнения системы (7), потому что ранг А = ранг В. В данном случае этот результат очевиден без применения теории о рангах матриц. Коэффициенты уравнений (7) вместе с их правыми частями соответственно пропорциональны, поэтому ясно, что всякое решение одного из этих уравнений является также решением другого.

Пример 4. Система

32

имеет определитель

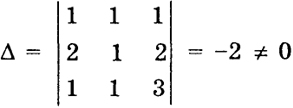
и поэтому имеет единственное решение, которое можно вычислить по формулам

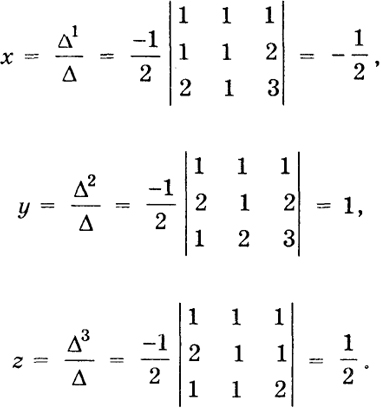
Пример 5. Система

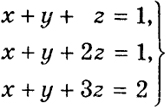
имеет определитель

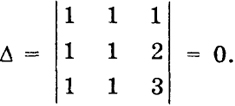
33

Матрица

имеет ранг А = 2, так как Δ = 0, но имеется определитель второго порядка, порожденный матрицей А, не равный нулю. Например,

Матрица

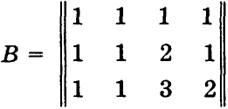
имеет ранг В = 3, так как определитель, порожденный этой матрицей,

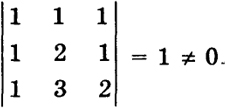
Так как ранг В > ранг А, то система не имеет решения.

Пример 6. Система

(10)

имеет определитель

34

Легко подсчитать, что матрицы

имеют равные ранги, причем ранг А = ранг В = 2. Выберем из системы (10) два уравнения так, чтобы ранг матрицы А' из коэффициентов этих уравнений был равен 2. В данном случае можно взять первое и второе уравнения или первое и третье. Итак, рассмотрим систему

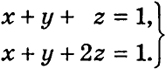(11)

Перенесем в правые части этих уравнений одно из неизвестных так, чтобы коэффициенты при оставшихся неизвестных образовывали матрицу А'' у которой ранг А'' = 2. В данном случае можно перенести или х или у. Итак, неоднородная система

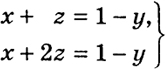(12)

имеет определитель

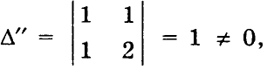
поэтому она имеет единственное решение при любой правой части:

35

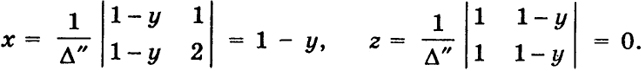(13)

Таким образом, тройки чисел (1 - у, у, 0) при всяком у ∈ (-∞, ∞) дают все решения системы (12) и автоматически решения третьего уравнения системы (10) (это уравнение получается из второго умножением на 2).

4.6. Обоснование правил.

Теорема 4. Если система (1) совместна, т. е. имеет хотя бы одно решение х, то необходимо ранг В = ранг А.

Теорема 4 дает обоснование правилу 1) (стр. 29), по которому, если ранг В > ранг А, то не выполняется необходимое условие совместности (непротиворечивости) системы (1).

Доказательство теоремы 4. Пусть система (1) имеет решение и ранг А = k. Нам надо доказать, что ранг В = k. Так как по условию ранг А = k, то существует не равный нулю определитель k-ro порядка, порождаемый матрицей А, следовательно и матрицей В. Поэтому ранг В > k. Остается доказать, что всякий определитель (k + 1)-го порядка, порождаемый матрицей В, равен нулю. Если такой определитель состоит только из элементов a_ij то он заведомо равен нулю, потому что он порождается также и матрицей А, которая по условию имеет ранг А. Таким образом, нужно доказать, что любой определитель (А + 1)-го порядка, порождаемый матрицей В и содержащей в себе столбец из чисел у}, равен нулю. Не нарушая общности, можно считать, что это определитель

К этому можно свести любой случай, перенумеровывая соответствующим образом уравнения и неизвестные х_j По условию система (1) совместна, т. е. существует вектор х₁ = (х₁..... х_n), удовлетворяющий уравнениям этой системы. Но тогда х, в

36

частности, удовлетворяет первым k + 1 уравнениям заново перенумерованной системы. Следовательно,

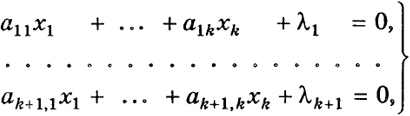(13)

где

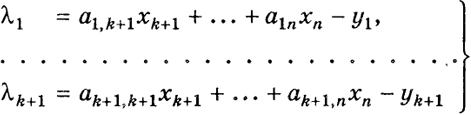(14)

Составим систему с неизвестными z₁ z₂, ..., z_k+1:

(15)

На основании (13) и (14) эта система удовлетворяется числами x₁..., x_k, 1, среди которых во всяком случае одно не равно нулю. Но тогда определитель однородной системы (15) равен нулю (см. теорему 3), т, е,

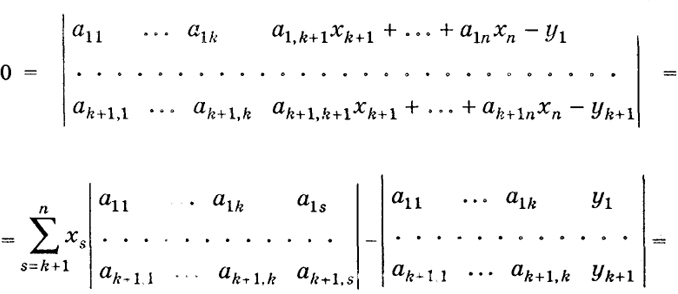
37

(16)

потому что определители ((k + 1)-го порядка!), входящие в сумму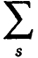, равны нулю - ведь ранг матрицы А равен k.

Мы доказали, что любой определитель (k + 1)-го порядка, порождаемый матрицей В, равен нулю, что и требовалось доказать.

Перейдем теперь к обоснованию правила 2) (стр. 29). Так как ранг матрицы А равен k (ранг А = k), то система (1) содержит k уравнений, матрица коэффициентов которых порождает не равный нулю определитель k-ro порядка. Перенумеровывая заново уравнения и неизвестные, можно достигнуть того, что первые k уравнений системы (1)

(1')

будут иметь определитель

Перенумерованную систему (1') перепишем еще так:

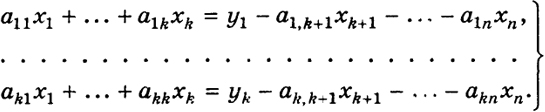(17)

38

В силу того, что определитель а ≠ 0, любой системе чисел x_k+l, ..., х_п соответствует единственная система чисел x₁, ..., x_k, которые, очевидно, можно записать следующим образом:

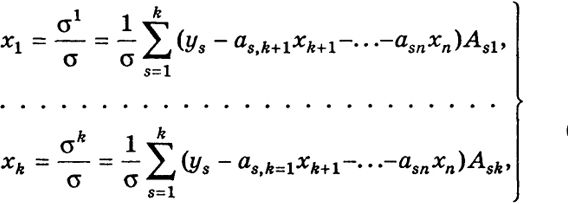(18)

где A_si - адъюнкты элементов a_si в определителе σ. Следовательно, все решения системы (17) записаны по формуле (18). Числам x _k+1, ..., х_п можно придавать любые значения, а числа x₁, ..., x_k будут вычисляться по формулам (18). Отсюда мы видим, что система (17) имеет бесконечное множество решений.

Мы хотим обосновать, что, если ранг А = ранг B = k, то любое найденное нами решение х первых k уравнений системы (1) автоматически является решением остальных уравнений этой системы. Для определенности докажем, что оно является решением (k + 1)-го уравнения. Итак, рассмотрим первые (k + 1) уравнений системы (1), которые мы запишем в виде (13). Надо доказать, что всякое решение х первых k уравнений (13) автоматически является решением (k + 1)-го уравнения в (13). Пусть х есть вектор, удовлетворяющий первым k уравнениям в (13). Составим уравнения (15) относительно неизвестных z ₁, ..., z _k+1, где числа λ₁, ..., λ _k+1 вычисляются по формулам (14) через компоненты x _k+1, ..., х_п вектора х. Определитель системы (15) равен нулю. Это видно из равенств (16), которые надо читать справа налево. По условию определитель справа равен нулю. Но тогда система (15) имеет нетривиальное решение z₁ z ₂, ..., z _k+1. Здесь число z_k+l ≠ 0, потому что, если допустить, что система (15) имеет решение вида z₁, ..., z_k, 0, то числа z ₁, ..., z_k должны обратиться в нули, потому что определитель σ ≠ 0. Но тогда z₁ - ... = z_k = z _k+1 =0 и система z₁, ..., z _k+1. была бы тривиальной. Вследствие

39

однородности системы (15) не только числа z₁, ..., z_k+l удовлетворяют этой системе, но и числа (z _k+1 ≠ 0)

z'₁ = z₁/z _k+1, …, z' _k = z_k/z _k+1, 1

обладают тем же свойством. Но тогда числа z'₁, ..., z' _k удовлетворяют системе первых k уравнений (13), имеющей определитель а σ ≠ 0. Мы уже знаем, что эта последняя система имеет решения x₁ ..., x_k и в силу единственности

z'₁ = x₁, ..., z' _k = x_k.

Обращаясь к последнему уравнению (15), мы видим, что оно удовлетворяется числами (x₁,..., x_k, 1), т. е. числа (x₁ ..., x_k) удовлетворяют (k + 1)-му уравнению системы (13), и в силу (14) рассматриваемый нами вектор х = (x₁,..., x_k, x _k+1, ..., х_п) удовлетворяет (k + 1)-му уравнению системы (1). Этим утверждение 2) доказано.

4.7. Метод решения системы путем исключения неизвестных. Можно рекомендовать следующий метод решения систем линейных уравнений, который является методом исключения неизвестных (или методом Гаусса¹). Пусть дана система

(1'')

Если мы умножим какое-либо уравнение системы (1'') на постоянное число и прибавим его к другому уравнению системы, то получим новую систему, эквивалентную прежней. Новая система уравнений будет иметь свою матрицу В', соответствующим образом преобразованную из матрицы В (В ⇒ В'). Преобразование заключается в том, что некоторая строка матрицы В видоизменяется прибавлением к ней другой строки, умноженной на соответствующее число.

40

Подобным образом, если умножить какое-либо из уравнений системы на число k ≠ 0, оставив остальные уравнения прежними, то получим новую систему, очевидно, эквивалентную исходной. Новая система будет иметь свою матрицу В', соответствующим образом преобразованную из матрицы В (В ⇒ В'). На этот раз преобразование заключается в том, что строка, соответствующая указанному уравнению, умножается на k.

Появляется также необходимость переставлять местами два уравнения системы (1''), получив, таким образом, формально новую, но эквивалентную исходной систему. В этом случае преобразование B ⇒ В' сводится к перестановке местами двух строк матрицы В.

Указанные три преобразования В => В' называют элементарными преобразованиями матрицы.

Технически, вместо того чтобы писать новую систему уравнений, ограничиваются тем, что пишут только соответствующую ей матрицу В'. Всегда можно, применяя подходящим образом элементарные операции над системой уравнений или, что все равно, над матрицей В, добиться либо решения заданной системы (1''), либо прийти к явно противоречивой системе. Так как последняя эквивалентна системе (l''), то это докажет противоречивость системы (1'').

Ниже приводятся примеры применения этого метода.

Операция В ⇒ В' обозначает, что В' получается из В посредством одной или нескольких элементарных преобразований.

Пример 7. Решить систему

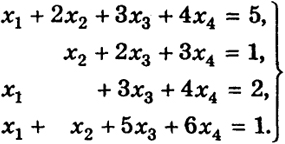
Конечно, согласно теореме 1, мы могли бы просчитать все пять определителей четвертого порядка и найти x₁, х₂, х₃, х₄. Здесь было бы много повторяющихся вычислений.

41

Составим матрицу В:

где, как мы видим, последний столбец состоит из правых частей нашей системы. Умножая первую строку на (-1) и прибавляя ее к третьей и четвертой строкам, получим матрицу

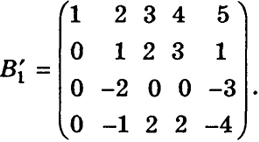
В матрице В

'

1

элементы третьей строки, являющиеся коэффициентами при неизвестных, кроме одного, равны нулю. Переместим эту строку на место второй строки. Тогда элемент, не равный нулю, окажется на главной диагонали:

Вторую строку можно еще умножить на (-1). чтобы запись была проще:

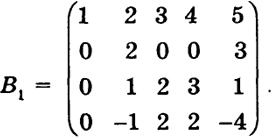
42

Дальнейшие преобразования матриц очевидны:

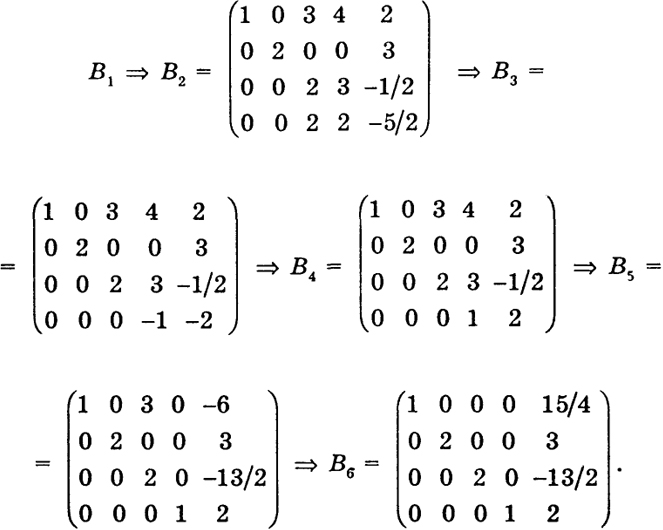
Отсюда x₄ = 2, х₃ = -13/4, х₂ = 3/2, х₁ = 15/4. Чтобы не допустить ошибки, рекомендуется осуществить проверку, подставив полученные значения в исходные уравнения системы.

Рассмотрим с этой точки зрения пример 5:

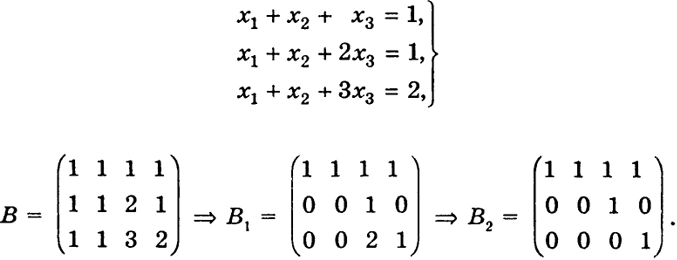
43

Таким образом, исходная система эквивалентна следующей:

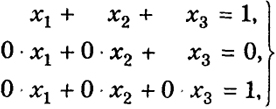
В последней строке свободный член равен единице, а коэффициенты при неизвестных равны нулю, поэтому система несовместна. Наконец, в примере 6

Отсюда

х₃ =. 0, x₁ + х₂ = 1,

т. е. система имеет бесконечное множество решений:

x₁ = x₁, х₂ = 1 - x₁, х₃ = 0,

где х₁ - любое число (-∞ < x₁ < ∞).

4.8. Нахождение ранга матрицы. Если нас интересует только вопрос о ранге матрицы В, то указанные выше элементарные операции В ⇒ B' распространим не только на строки, но и на столбцы матрицы. При этом, если в процессе этих преобразований в матрице появляются строка или столбец, целиком состоящие из нулей, то их надо удалить из матрицы, т. е. рассматривать далее матрицу меньшего размера.

44

Следующие примеры иллюстрируют этот метод. Пример 8. Найти ранг матрицы

Ясно, что ранг матрицы В не больше 4. В данном случае а₁₁ = 1 ≠ 0. Умножая первую строку на (-1) и прибавляя ее к третьей строке, получаем

Теперь, умножая первый столбец на соответствующие числа и прибавляя его к остальным столбцам, получим матрицу

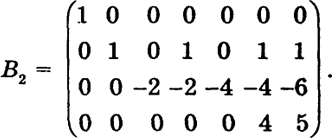
Второй столбец уже состоит из нулей, кроме элемента а₂₂ = 1 ≠ 0. Умножая второй столбец на (-1) и прибавляя его к 4, 6, 7 столбцам, получим

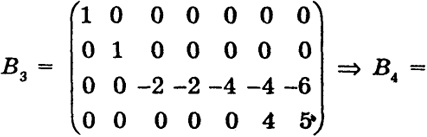
45

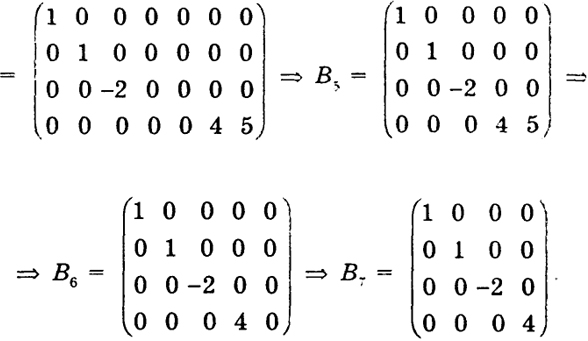
Определитель четвертого порядка матрицы В₇ не равен нулю, следовательно, ранг В = ранг В₇ = 4.

Пример 9. Найти ранг матрицы

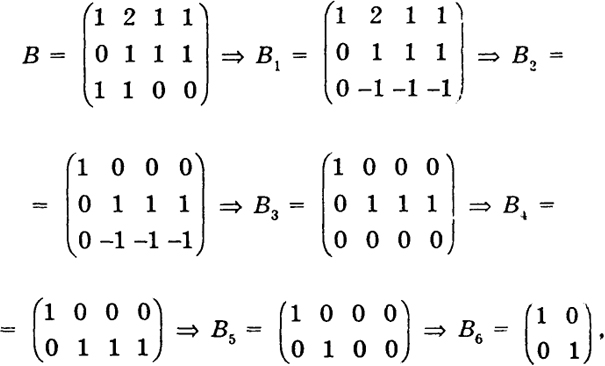
т. е. ранг матрицы В равен двум.

Рассуждения в примерах 8 и 9 основаны на следующем общем утверждении: при элементарном преобразовании В ⇒ В' ранг матрицы сохраняется, т. е. выполняется равенство

ранг В = ранг В'.

46

Это утверждение очевидно, если элементарное преобразование сводится к замене местами строк или столбцов матрицы или к выкидыванию из матрицы ее строки или столбца, состоящих из нулей.

Остается еще один случай, который мы выразим в виде теоремы.

Теорема 5. Пусть матрица В подвергнута преобразованию В ⇒ В', заключающемуся в том, что к некоторой ее строке (столбцу) прибавляется другая какая-либо строка (столбец), умноженная на число С.

Тогда ранги матриц В и В' равны.

Доказательство. Будем доказывать эту теорему для строк (для столбцов рассуждения аналогичны).

Пусть k есть номер строки матрицы В - (b_kl), умножаемой на число С и прибавляемой к другой строке В, которую будем считать имеющей номер l (таким образом, l-я строка матрицы В' состоит из элементов Cb_kj + b_ij, j = 1, ..., n). Пусть

ранг В = r, ранг В' = r'.

Достаточно показать, что r' ≤ r, потому что по аналогии доказывается также, что r ≤ r', откуда r = r'.

Если r = 0, то все элементы матрицы В равны нулю и, следовательно, равны нулю все элементы матрицы В', откуда r = r' = 0.

Пусть теперь r > 0. Тогда существует матрица А порядка r, порождаемая матрицей В, с неравным нулю определителем (|А| ≠ 0), а все матрицы А, порождаемые В, порядка, большего г, имеют определители, равные нулю. При преобразовании В ⇒ В' матрица А преобразуется в некоторую матрицу А' (А ⇒ А'). Пусть матрица А имеет порядок, больший r.

Если l-я строка матрицы В не участвует в образовании A, то, очевидно, А = А' и 0 = |А| = | А '|.

47

Если в образовании А участвуют обе строки В с номерами k и l, то 0 = |A| = |А'|. Ведь чтобы получить определитель |A'|, надо к некоторой строке определителя |А| прибавить определенную другую его строку, умноженную на число C, от чего величина определителя не меняется.

Наконец, пусть в образовании матрицы А участвует l-я. строка, но не участвует k-я строка. Очевидно (см. свойство з) определителя),

|А '| = | А | + С|Λ|, (19)

где Λ - матрица порядка, большего r, получаемая из А заменой элементов l-й строки на соответствующие элементы k-й строки матрицы В. Но такая замена не меняет ранг В и так как | А | = 0, то |Λ| = 0.

Из (19) получаем |А'| = 0 + С ∙ 0 = 0.

Мы пересмотрели все случаи, когда матрица А' имеет порядок, больший чем r, и всякий раз оказывалось, что | А '| = 0. Это показывает, что

r' = ранг В' ≤ r,

что и требовалось доказать.

48

---