24.1. Общее уравнение кривой второго порядка. В плоскости, в некоторой прямоугольной системе координат х, у, пусть задана кривая, определяемая неявно уравнением второй степени
178
Ах2 + 2Вху + Су2 + 2Dx + 2Еу + F = 0, (1)
где A, В, С, D, Е, F - заданные действительные числа. При этом числа А, В, С одновременно не равны нулю. Эта кривая называется кривой второго порядка. На самом деле может случиться, что нет вовсе точек (х, у) с действительными координатами, удовлетворяющих уравнению (1). В этом случае говорят, что уравнение (1) определяет мнимую кривую второго порядка. Мы не будем изучать мнимые кривые. Уравнение
х2 + у2 = -1
может служить примером уравнения второй степени, определяющего мнимую кривую.
24.2. Важные случаи общего уравнения кривой второго порядка. Перечислим шесть важнейших частных случаев общего уравнения (1):
1) Уравнение эллипса
+
= 1 (
a, b > 0)
с полуосями длины а и b. В частности, при а = b уравнение окружности
х2 + у2 = а2
с центром в начале координат и радиусом а.
2) Уравнение гиперболы
-
= 1 (
a ≥
b ≥ 0)
с полуосями а и b.
3) Уравнение параболы
у2 = 2рх (р > 0).
179
4) Уравнение пары пересекающихся прямых
а2х2 - b2у2 = 0 (0 < а, b).
5) Уравнение пары параллельных или совпадающих прямых
х2 - а2 = 0 (а ≥ 0).
6) Уравнение, определяющее точку,
х2 + у2 = 0.
Остановимся вкратце на перечисленных кривых.
Эллипс
+
= 1 (
a ≥
b > 0) (2)
При а = b эллипс (2) обращается в окружность радиуса а с центром в начале координат, т. е. геометрическое место точек, отстоящих от начала на расстоянии а.
Пусть а > b. Положим с = √a2 - b2. Отметим на оси х точки F1, F2, имеющие абсциссы х = -с и х = с. Это фокусы эллипса. Эллипс (2) можно определить как геометрическое место точек, сумма расстояний которых до фокусов F1, F2 есть величина постоянная, равная 2а.
В самом деле (рис. 37),
MF1 = √(x + c)2 + y2, MF2 = √(x - c)2 + y2,
2a = √(x + c)2 + y2 + √(x - c)2 + y2,
откуда
2a - √(x + c)2 + y2 = √(x - c)2 + y2
и
4a2 + (x + c)2 + y2 - 4a√(x + c)2 + y2 = (x - c)2 + y2,
180
4a2 + 4cx = 4a√(x + c)2 + y2,
a2 + 2a2cx + c2x2 = a2[x2 + 2cx + c2 + y2],
-b2x2 = -a2b2 + a2y2,
a2b2 = b2x2 + a2y2,
откуда следует уравнение (2). Если проследить эти выкладки в обратном порядке, то получим, что если точка (x, y) удовлетворяет уравнению (2), то сумма ее расстояний до F1 и F2 равна 2а.
Если в уравнении (2) заменить х на -х, то оно не изменится - это показывает, что эллипс (2) есть кривая, симметричная относительно оси у. Аналогично эллипс (2) симметричен относительно оси х, потому что его уравнение не изменяется при замене у на -у. Но тогда достаточно изучить его уравнение в первой четверти (системы координат), т. е. для х, у ≥ 0. Часть эллипса, находящаяся в первой четверти, определяется уравнением
у =
√a2 - x2 (0 ≤
х ≤
а).
Из этого уравнения видим, что наш эллипс проходит через точки (0, b) и (а, 0). При этом его ордината у при непрерывном возрастании х на отрезке [0, а] непрерывно убывает.
Эллипс - ограниченная кривая. Он находится внутри круга радиуса а с центром в начале координат (для координат любой точки эллипса (х, у) имеет место неравенство
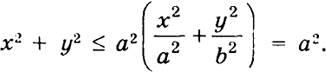
Из рис. 37 мы видим, что эллипс есть непрерывная замкнутая кривая. В первой четверти это выпуклая вверх
181
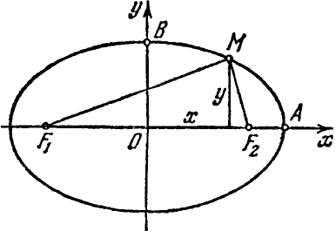
Рис. 37
кривая. В любой ее точке можно провести касательную1. Все эти свойства и многие другие могут быть с успехом изучены методами математического анализа, который к тому же дает средства для точного определения высказанных выше понятий - непрерывность, выпуклость и т. д.
Уравнение эллипса можно записать еще в параметрической форме
 (3)
(3)
В самом деле
+
= cos
2θ + sin
2θ = 1
т. е. точка (х, у), определяемая равенствами (3) при любом 0 принадлежит эллипсу (2). Если G непрерывно пробегает полуинтервал [0, 2π), то точка (х, у) описывает полный эллипс. При дальнейшем возрастании 0 движение периодически повторяется.
Выясним смысл параметра 9 и попутно укажем способ построения эллипса (рис. 38). Проведем две концентрических
182
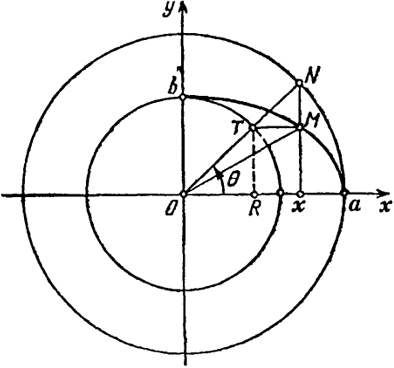
Рис. 38
окружности радиусов b и а (b < а) с центром в точке О. Затем проведем радиус-вектор под углом θ к оси х и обозначим его точки пересечения с окружностями радиуса b и а соответственно Т и N. Из точки N проведем прямую, параллельную оси у, а из точки Т - прямую, параллельную оси х. Точка пересечения этих прямых М принадлежит эллипсу. В самом деле, пусть х - абсцисса точки М, а у - ордината этой точки. Тогда (см. рис. 38)
х = ON ∙ cos θ = a cos θ,
у = TR = ОТ ∙ sin θ = b sin θ,
т. е. точка М действительно находится на эллипсе (3) и параметр θ есть угол между осью х и лучом ON. Отметим, что θ не является полярным углом φ, который образует радиус-вектор ОМ с осью х (tg φ =
tg θ). Например, если φ = π/4,
а =
√3 ,
b = 1, то θ = π/3; если φ = 0, то θ = 0; если φ = π/2, то θ = π/2.
183

Рис. 39
Гипербола
-
= 1 (0 <
a, b) (4)
Положим с = √a2 + b2 и отметим на оси х точки F1 и F2 - фокусы гиперболы (4), имеющие абсциссы x = -с и x = с (рис. 39).
Гипербола (4) может быть определена также как геометрическое место точек А = (х, у), разность расстояний которых до фокусов F1 и F2 есть величина постоянная, равная 2а.
Имеем (см. рис. 39)
AF1 - AF2 = √(x + c)2 + y2 - √(x - c)2 + y2 = 2a,
√(x + c)2 + y2 = √(x - c)2 + y2 + 2a,
4cx - 4a2 = 4a√(x - c)2 + y2,
b2x2 - a2y2 = a2b2
откуда следует уравнение (4).
184
Мы получили правую ветвь гиперболы (см. рис. 39). Чтобы получить левую ветвь, надо исходить из равенства
AF2 - АF1 = 2а.
Рассуждениями, проведенными в обратном порядке, можно заключить, отправляясь от уравнения (4), что точки (х, у) ему удовлетворяющие, принадлежат к указанному выше геометрическому месту.
По виду уравнения (4) заключаем, что гипербола (4) симметрична относительно оси х и оси у. Часть гиперболы (4), находящаяся в первой четверти, имеет уравнение
у =
√x2 - а2 (
а ≤
х < ∞). (5)
Мы видим, что наша гипербола проходит через точку (а, 0) и при возрастании х на полуинтервале [а, ∞) ордината у возрастает и стремится к бесконечности. Точки В = (-а, 0) и С = (а, 0), в которых гипербола пересекает ось х, называются вершинами гиперболы.
На рис. 39 нарисованы две прямые:
у = ±
х.
Это асимптоты нашей гиперболы.
Пусть на полуинтервале [а, ∞) (или (-∞, а]) задана кривая у = f(x). Говорят, что прямая у = тх + п есть асимптота этой кривой при х → +∞ (х → -∞), если
[
f(
x) -
тх -
п] = 0
(соответственно
[
f(
x) -
тх -
п] = 0).
Рассмотрим кусок нашей гиперболы, определяемый равенством (5), и сравним его с прямой у =
х. Предел
185

Это показывает, что прямая у =
х есть асимптота рассматриваемого куска гиперболы при
х → +∞. Но тогда говорят, что прямая
у =
х есть асимптота (всей!) гиперболы при х → +∞. В силу симметрии нашей гиперболы относительно осей, так же как симметрии пары прямых
у = ±
х относительно осей, можно сказать, что обе эти прямые являются асимптотами нашей гиперболы и притом как при х → +∞, так и при х → -∞.
Правая ветвь гиперболы (4) может быть записана в параметрическом виде
 (6)
(6)
В самом деле, так как
ch2u - sh2u = 1 (7)
то из уравнений (6) получим
-
= ch
2u - sh
2 u = 1
Верхняя половина правой ветви гиперболы соответствует изменению и ∈ [0, ∞), а нижняя - изменению и ∈ (-∞, 0].
186
Выясним, как параметр и связан с параметром θ в параметрическом уравнении эллипса, и попутно укажем способ построения гиперболы с помощью циркуля и линейки. Так как наш способ построения гиперболы будет основан на способе построения эллипса, то мы изложим эти два способа построения совместно (рис. 40). Ограничимся построением частей эллипса (2) и гиперболы (6), находящихся в первой четверти. Проведем две концентрические окружности радиуса а и b с центром в начале координат. Проведем луч, выходящий из начала координат под углом θ0 к оси х. Пусть Т1 и Nl - точки пересечения этого луча с указанными окружностями (ОТ1 = b, ON1 = а). Проводя из точек Т1 и N1 прямые, параллельные осям х и у соответственно, получим точку их пересечения Мэ = (х0, у0), принадлежащую эллипсу (2). Затем проводим луч ОМЭ. Пусть N2 - точка пересечения этого луча с окружностью радиуса а; Р - точка пересечения этого луча с прямой, параллельной оси у и проходящей через точку эллипса А=(а, 0). Уравнение луча ОР можно записать:
y =
x
Отсюда следует, что ордината точки Р равна Y0 =
. Далее соединим точку
B1 = (
х0, 0) с точкой
N2 и из точки
А
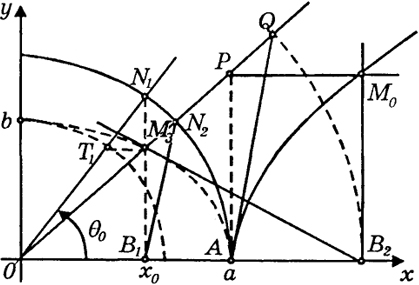
Рис. 40
187
проведем прямую, параллельную B1N2, которая пересечет луч ОР в точке Q.
Из подобия треугольников OAQ и ОВ1N2 получим, что OQ = а2BREAK/х0. Радиусом OQ на оси х отмечаем точку В2=(а2BREAK/х0, 0).
Теперь из точек В2 и Р проводим прямые, параллельные осям у и х соответственно. Точка пересечения этих прямых Мr = (X0, Y0), где X0 = а2BREAK/x0 принадлежит гиперболе (4).
В самом деле, так как точка (х0, y0) лежит на эллипсе (2), то
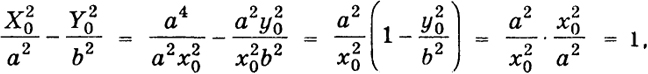
т. е. точка Мr принадлежит гиперболе (4).
Отметим, что точка В2 = (а2BREAK/х0, 0) является точкой пересечения касательной к эллипсу в точке Мэ с осью х (см. сноску на стр. 139).
Таким образом, каждой точке (х, у) эллипса (2) соответствует вполне определенная точка (X, Y) гиперболы (4) и обратно.
Теперь, если эллипс (2) задан параметрически, то
х = a cos θ, у = b sin θ.
Поэтому
X =
=
,
Y =
=
b tg θ.
Отсюда, учитывая (6), получаем
ch u =
, sh
u = tg θ.
Имеют место также следующие формулы:
tg
=
√ =
√ = tg
;
eu = ch u + sh u =
+ tg θ =
=
188

т. е.
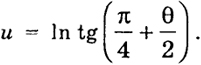
Парабола
у2 = 2рх (р > 0). (8)
Отметим на оси х точку F с абсциссой х = р/2, называемую фокусом параболы (8), и проведем прямую х = -р/2, называемую директрисой параболы (8) (рис. 41).
Парабола (8) может быть еще определена как геометрическое место точек А = (х, у), равноудаленных от фокуса и директрисы. В самом деле (см. рис. 41)
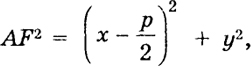
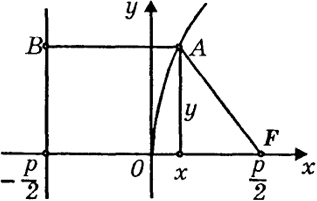
Рис. 41
189

следовательно.
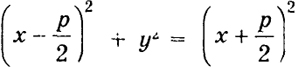
т. е.
у2 = 2рх.
Обратно, из этого уравнения следует, что точки, ему удовлетворяющие, принадлежат к указанному геометрическому месту точек.
Из уравнения (8) видно, что парабола (8) симметрична относительно оси х. Ее верхняя половина имеет уравнение
у = √2px (0 ≤ х < ∞), (9)
из которого видно, что когда х пробегает полуинтервал [0, ∞) возрастая, ордината у возрастает от 0 до ∞.
Укажем простой способ построения параболы (9) с помощью линейки и прямого угла или с помощью циркуля и линейки. Проведем прямую х = -2р (рис. 42). Возьмем на этой прямой произвольную точку К = (-2р, у), у > 0. Соединим эту точку с началом координат и проведем прямую, проходящую через начало координат, перпендикулярную к прямой ОК. Далее проводим прямую через точку К параллельно оси х. Последние две прямые пересекаются в точке М = (х, у), которая принадлежит параболе (9), так как ОА = у есть среднее геометрическое чисел 2р и х (у = √2рх ).
Парабола (8) не имеет асимптот1.
190
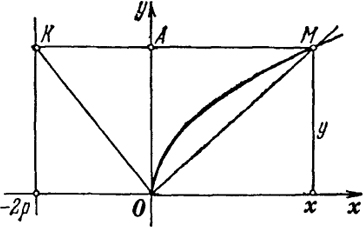
Рис. 42
Пара пересекающихся прямых
а2х2 - b2у2 = (ах - bу)(ах + by) = 0 (0 < at b). (10)
Если какая-либо точка (х, у) удовлетворяет уравнению (10), то она удовлетворяет одному из уравнений
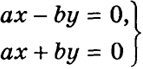 (10’)
(10’)
или обоим. Обратно, если точка (х, у) удовлетворяет одному из уравнений (10'), то она удовлетворяет и уравнению (10). В этом смысле говорят, что (10) есть уравнение пары прямых.
24.3. Классификация кривых второго порядка
Ниже будет доказано, что существует прямоугольная система координат такая, что в ней кривая (1), если она не мнимая, имеет одно из перечисленных выше уравнений 1) - 6).
Более детально:
- при АС - В2 > 0 кривая (1) есть эллипс, точка (случаи 1), 6)) или мнимая кривая;
- при АС - В2 < 0 кривая (1) есть гипербола или пара пересекающихся (разных) прямых (случаи 2), 4));
191
- при AC - В2 = 0 кривая (1) есть парабола, пара параллельных или совпадающих прямых или мнимая кривая (случаи 3), 5)).
Мы позволяем себе говорить "кривая" даже и в случаях 4), 5), 6), когда речь идет о паре прямых или множестве, состоящем из одной точки.
Итак, пусть задано уравнение
Ах2 + 2Вху + Су2 + 2Dx + 2Еу + F = 0, (1)
где коэффициенты А, В, С одновременно не равны нулю.
Не нарушая общности, можно считать, что А ≥ 0, А ≥ С, В ≥ 0. К этой ситуации всегда можно прийти с помощью ортогональных преобразований:
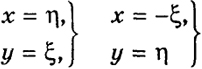
и умножения левой и правой частей (1) на - 1.
Если В = 0, А ≥ С ≥ 0, то (1) можно записать в виде
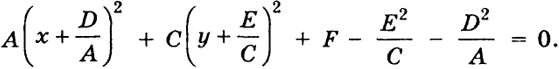
Параллельный перенос
ξ = x +
, η =
y +
преобразует уравнение (11) следующим образом:
Aξ2 + Cη2 =
+
-
F. (11')
Если число -
+
-
F > 0, то уравнение (11') представляет собой уравнение эллипса (случай 1)) с полуосями
а, b, где
192

Отметим, что в данном случае АС - В2 = АС > 0.
Если же правая часть уравнения (11') равна нулю, то мы получаем точку (случай 6)).
При отрицательной правой части уравнение (11') дает мнимую кривую.
Если число С = 0, А > 0, то (1) можно записать в виде
 (12)
(12)
Пусть число Е ≠ 0, тогда параллельный перенос
ξ = x +
, η =
y +
-
преобразует уравнение (12) в уравнение
Аξ2 + 2Еη = 0, (12')
которое (после замены, если нужно, η на -η) представляет собой уравнение параболы (случай 3))"
Если Е = 0, то в зависимости от знака числа
- F, мы получим пару параллельных прямых или мнимую кривую. Отметим, что здесь
АС -
В2 = 0.
Далее, если число С < 0, А > 0, то уравнение (1) можно записать:

анализ которого проводится так же, как в случае уравнения (11). Уравнение (13) дает гиперболу или пару пересекающихся прямых (случаи 2) и 4)). Отметим, что в данном случае АС - B2 = АС < 0.
193
Случай А = 0, С < 0 сводится к уравнению типа (12).
Итак, при В = 0 уравнение (1) всегда дает один из частных случаев 1)-6).
Пусть теперь В > 0, А ≥ С. Тогда, как мы знаем (см. § 23), существует ортогональное преобразование
 (14)
(14)
где

которое приводит квадратичную форму
Ах2 + 2Вху + Су2
к каноническому виду.
Преобразуем уравнение (1) с помощью (14):
λ1ξ2 + λ2η2 + D(x1ξ - у1η) + Е(у1ξ + х1η) + F = 0, (15)
где

(λ1 > λ2,λ1λ2 = АС - B2). Перепишем уравнение (15) в виде λ1ξ2 + λ2η2 + (x1D + у1Е)ξ + (х1Е - y1D)η + F = 0. (15’)
Уравнение (15') является частным случаем уравнения (1) при В = 0, которое мы уже исследовали.
Таким образом, мы можем сказать, что если:
194
- 1) AC - В2 = λ1λ2 > 0, то уравнение (1) представляет собой эллипс, точку или мнимую кривую. В этом случае будем говорить, что уравнение (1) принадлежит эллиптическому типу;
- 2) АС - В2 = λ1λ2 < 0, то уравнение (1) представляет собой гиперболу или пару пересекающихся прямых. В этом случае будем говорить, что уравнение (1) принадлежит гиперболическому типу;
- 3) АС - В2 = λ1λ2 = 0, то уравнение (1) изображает параболу, пару параллельных прямых или мнимую кривую, В этом случае будем говорить, что уравнение (1) принадлежит параболическому типу.
Пример 1. Выяснить характер кривой
2х2 + √3 ху + у2 + 2х + 2√3 у + F = 0,
где F - произвольное действительное число.
В данном случае А = 2 > С = 1, В =
> 0,
АС -
В2 = > 0, т. е. уравнение принадлежит эллиптическому типу. Легко подсчитать (см. пример в § 23), что
x1 =
,
y1 =
, λ
1 =
, λ
2 =
.
Поэтому с помощью ортогонального преобразования
x =
(
√3ξ - η),
y =
(ξ +
√3η)
наше уравнение запишется
195
ξ
2 +
η
2 + (
√3ξ - η) +
√3(ξ +
√3η) +
F = 0
или
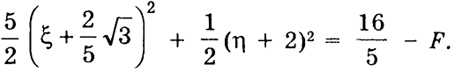
Осуществим еще параллельный перенос
u = ξ +
√3,
v = η + 2,
тогда будем иметь
u2 +
v2 =
-
F. (16)
Если
- F > 0, то (16) будет уравнением эллипса с 5 полуосями
а,
b, где
а2 = 2(16 - 5F)/25, b2 = 2(16 - 5F)/5.
Если
-
F = 0, то (16) дает точку. Если
-
F < 0, то (16) представляет мнимую кривую.
196
1См. нашу книгу "Высшая математика. Дифференциальное и интегральное исчисление", §4.2.
1См. нашу книгу "Высшая математика. Дифференциальное и интегральное исчисление", § 4.20.
