§ 22. Самосопряженный оператор. Квадратичная форма

Линейный оператор

y_k =

n

∑

l=1

 a_klx_l (k = 1, …, n) (1)

или, коротко,

у = Ах (х ∈ R_n, у ∈ R_n) (2)

называется самосопряженным, если он равен своему сопряженному (А = А*), т. е. если

161

Ах = А*х ∀x ∈ R_n, (3)

иначе говоря, если матрица А симметрическая:

a_kl = a_lk (k,l = 1, …, n) (4)

(см. (3) и (3*) § 21). Мы считаем а_kl и R_n действительными (см. ниже замечание 1).

Для самосопряженного оператора имеет место характерное равенство

(x, Аz) = (Ах, z) ∀x, z ∈ R_n

(см. § 21, (4)). Очевидно,

(x, A_z) =

n

∑

k=1

 x_k

n

∑

l=1

 a_klx_l =

n

∑

k=1

 

n

∑

k=1

 a_klx_kx_l (a_kl = a_lk). (4')

Выражение справа в (4') называется квадратичной формой n-го порядка. Это непрерывная функция от вектора х или, что все равно, от переменных x₁, ..., х_п.

Будем рассматривать эту функцию на множестве S значений х, имеющих единичную норму (|х| = 1). Множество S есть сфера в R_n радиуса 1 с центром в точке 0. S - ограниченное множество. Кроме того, оно замкнуто ¹): если точки последовательности {x^ν} (ν = 1, 2, ...) принадлежат к S (т. е. |x^v| = 1, ν = 1, 2, ...) и эта последовательность стремится к некоторой точке х⁰ ∈ R_n (x^ν → х⁰, ν → ∞), то неминуемо х⁰ ∈ S, т. е. |х⁰| = 1, потому что |1 -|x⁰|| = ||x^ν| - |x⁰|| ≤ |x^ν = x⁰| → 0, откуда |x⁰| - 1.

Найдем максимум квадратичной формы (4') на сфере S. Так как форма (4') есть непрерывная функция на замкнутом ограниченном множестве, то максимум ее на S достигается для некоторого единичного вектора х¹ (|x^l| = 1). Обозначим этот максимум через λ₁:

λ₁ = (Ах¹, х¹) ≥ (Ах, х) ∀ x : |х| = 1. (5)

Введем подпространство L', ортогональное к вектору x¹, т. е. множество всех векторов v, каждый из которых

162

ортогонален к х¹. В L’ возьмем произвольный единичный вектор v⁰ (|v⁰| = 1). Вектор

cos α ∙ х¹ + sin α ∙ v⁰

зависит от α и имеет единичную норму

|cos α ∙ х¹ + sin α ∙ v⁰| =
= (cos α ∙ х¹ + sin α ∙ v⁰, cos α ∙ х¹ + sin α ∙ v⁰)^1/2 =
= (cos²α + sin²α)^1/2= 1.

При α = 0 этот вектор обращается в х¹. Но тогда функция

ψ(α) = (A(cos α ∙ x^l + sin α ∙ v⁰), cos α ∙ x^l + sin α ∙ v⁰)

достигает своего максимума в точке α = 0 (ψ(0) = (Ах¹, х¹)) и в силу необходимого условия экстремума

ψ’(0) = 0.

Вычислим эту производную. Имеем

ψ(α) = cos²α(Ax¹, х¹) + sin²α(Ax¹, v⁰) + sin²α(Av⁰, v⁰).

Следовательно,

ψ’(α) = -sin²α(Ax¹, x¹) + 2cos²α(Ax¹, v⁰) + sin²α(Ax⁰, v⁰)

и

ψ’(0) = 2(Ax^l, v⁰) = 0.

Мы получили, что вектор Аx¹ ортогонален ко всем единичным векторам v⁰ ∈ L', следовательно, и к любым векторам v ∈ L'. Но тогда Аx¹ отличается от x¹ лишь множителем (см. следствие 1 в конце § 20), т. е.

Аx¹ = λx¹,

где λ - некоторое число.

Из первого соотношения (равенства) в (5), учитывая, что |x¹| = 1, следует

163

λ₁ = (λx¹, x¹) = λ.

Таким образом, мы доказали, что максимум квадратичной формы (4') на единичной сфере |х| = 1 достигается в некоторой точке х¹,

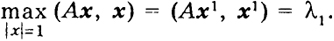
При этом

Ax¹ = λ₁x¹, |x¹| = 1

Мы видим, что нетривиальный (не равный нулю) вектор х¹ отображается при помощи оператора А в вектор λ₁x¹, ему коллинеарный.

Такой вектор называется собственным вектором оператора А, а число λ₁ - принадлежащим этому вектору собственным значением.

Будем теперь рассматривать оператор А на подпространстве R1, определяемом как множество векторов л: (е Rn), ортогональных к вектору х1 (выше мы его обозначали через L'). R1 есть (я - 1)-мерное подпространство - в нем имеются ортонормированные базисы, состоящие из п - 1 векторов. Цель наша заключается в подыскании одного такого базиса, как мы увидим, естественно связанного с оператором А.

Важно подчеркнуть, что образ A(R¹) подпространства R¹ при помощи оператора А принадлежит к R¹, потому что, если (х, х¹) = 0, то

(Ах, x¹) = (х, Ах¹) = (х, λ₁x¹) = λ₁(x, х¹) = 0,

т. е. Ах ∈ R¹.

Самосопряженность оператора А на R¹ тривиальным образом сохраняется, потому что равенство

(Ах, у) = (х, Ау),

верное для всех х, у ∈ R_n, верно также для всех х, у ∈ R¹.

164

Итак, мы теперь рассматриваем самосопряженный линейный оператор А на линейном подпространстве R¹ измерения п - 1. К нему можно применить приведенные выше рассуждения и обнаружить в R¹ существование единичного вектора х² такого, что

Дело в том, что единичная сфера S¹ в R¹ определяется, очевидно, как множество единичных векторов х, ортогональных к х¹. При этом

Ах² = λ₂х².

Мы нашли второй собственный вектор оператора А -вектор х² и принадлежащее к нему собственное значение λ₂, очевидно, не превышающее λ₁ (при уменьшении области рассмотрения максимум может только уменьшиться). При этом (х¹, х²) = 0.

Подобным образом можно ввести подпространство R², измерения п - 2, ортогональное к векторам х¹ и х², показать, что оператор А отображает R² в R² и определить третий единичный вектор х³, ортогональный к х¹ и к х² такой, что для него имеет место

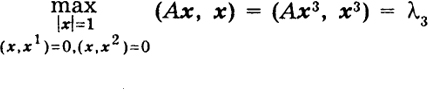
и

Ах³ = λ₃х³ (λ₃ ≤ λ₂ ≤ λ₁).

Продолжив этот процесс по индукции до n-го вектора х^п, мы получим ортонормированную систему векторов

λ¹, λ², …, λⁿ (6)

и систему действительных чисел

165

λ₁, λ₂, …, λ_n, (7)

обладающих свойствами

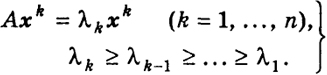(8)

Мы получили полную систему собственных векторов оператора А и принадлежащих им собственных значений. Так как ортонормированная система (6) принадлежит к R_n и состоит из п векторов, то она есть базис в R_n (см. § 17). Поэтому произвольный вектор x ∈ R_n можно разложить по этой системе:

x =

n

∑

k=1

 (x, x^k)x^k (9)

Тогда наш самосопряженный оператор А может быть записан следующим образом:

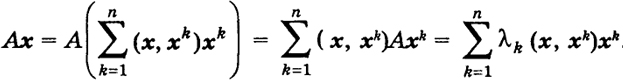
Мы доказали теорему.

Теорема 1. Самосопряженному оператору А в пространстве R_n соответствует ортогональная система векторов х¹,.... х^п (базис R_n) и система действительных чисел λ₁, …, λ_п такие, что Ах для любого х ∈ R_n представляется в виде суммы (10).

Квадратичная форма (4') соответственно записывается следующим образом:

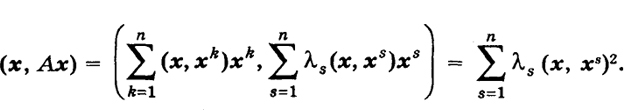
На практике часто мы исходим из некоторой квадратичной формы

166

n

∑

k=1

 

n

∑

l=1

 a_klx_kx_l (a_kl = a_lk)

Чтобы применить к ней полученные результаты, можно определить в связи с ней линейный оператор

y = Ах,

определяемый равенствами

y₁ =

n

∑

j=1

 a_ijx_j (i =1, …, n)

В силу условия a_kl = a_lk это самосопряженный оператор, и к нему применима теорема 1. На языке квадратичной формы теорема 1 может быть переформулирована следующим образом.

Теорема 2. Пусть задана квадратичная форма (4') в n-мерной системе координат x₁ ..., х_п пространства R_n с ортами i¹, ..., iⁿ 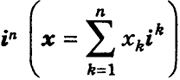. Существует прямоугольная система координат ξ₁, ..., ξ_n с ортами х¹, ..., х^п, образующими ортогональный базис 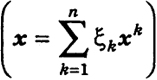, и система действительных чисел λ₁, …, λ_n такие, что квадратичная форма (4') в этой системе есть сумма квадратов координат ξ₈ вектора х, помноженных соответственно на числа λ₈:

n

∑

k=1

 

n

∑

l=1

 a_klx_kx_l =

n

∑

s=1

 λ_sξ

2

s

(4’’’)

167

Переход от левой части (4’’’) к правой можно осуществить, если известны разложения векторов x¹, ..., хⁿ по ортам i¹, ..., iⁿ. Пусть

x^j =

n

∑

s=1

 β_jsi^s

(см. § 17, (7), где надо заменить a_js, a^k соответственно на β_s, х^j). Так как i¹, ..., iⁿ и х¹ ..., х^п - ортонормированные базисы в R_n, то матрица

Λ = ||β_js||

ортогональная. Мы считаем, что она известна. Один и тот же вектор х можно разложить по двум базисам:

x =

n

∑

s=1

 x_si^s =

n

∑

j=1

 ξ_jx^j

Но тогда

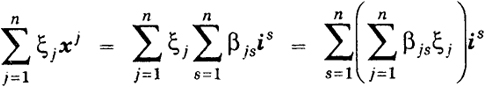
и в силу линейной независимости системы i¹, ..., iⁿ получим

x_s =

n

∑

j=a

 β_jsξ_j (s = 1, …, n) (11)

Таким образом, переход от координат ξ₁, ..., ξ_n к координатам x₁, ..., x_n осуществляется посредством матрицы Λ', транспонированной к Λ (т. е. с помощью строк матрицы Λ' или столбцов матрицы Λ).

Если подставить выражения (11) для х_s в левую часть (4’’’), то должны получить правую. Запишем это равенство:

168

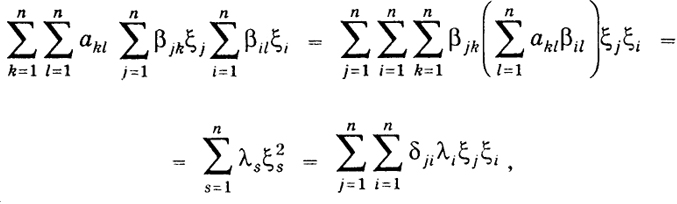
где 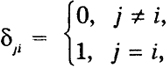- символ Кронекера.

Если приравнять коэффициенты при одинаковых ξ_jξ_i, то получим равенства

которые можно трактовать следующим образом (см. § 15, (6)). Для матрицы

А = ||a_kl|| (a_kl = a_lk)

самосопряженного оператора А существует ортогональная матрица

Λ = ||β_js||

такая, что

Λ ∙ A ∙ Λ^-1 = H,(12)

где H - некоторая диагональная матрица

H = (13)

(λ_i - действительные числа), называемая канонической.

169

Отметим, что для ортогональной действительной матрицы Λ

Λ^-1 = Λ'.

Так как определители ортогональных матриц |Λ| = |Λ^-1| = ±1, то из (12) следует

(14)

Мы доказали, в частности, следующую теорему.

Теорема 3. Если определитель |Λ| самосопряженной матрицы А не равен нулю (|Λ| ≠ 0), то все ее собственные числа λ₁, ..., λ_п не равны нулю (λ_j ≠ 0, j = 1, ..., п).

Из теоремы 2 следует, что

• 1) Если λ₁ ≥ ... ≥ λ_n > 0, то квадратичная форма положительная для любых векторов ξ ≠ 0, а следовательно, и любых векторов х ≠ 0. В этом случае она называется строго положительной.
• 2) Если 0 ≥ λ₁ ≥ λ₂ ≥ ... ≥ λ_n, то форма отрицательная для любых ξ ≠ 0, следовательно, и любых x ≠ 0. В этом случае она называется строго отрицательной.
• 3) Если λ₁ ≥ ... ≥ λ_n и λ_n = 0, то форма неотрицательная. Существует направление, (ось ξ_n), вдоль которого она равна нулю. Это положительная форма, но не строго.
• 4) Если λ₁ = 0 ≥ λ₁ ≥ ... ≥ λ_n, то форма отрицательная не строго.
• 5) Если λ₁ ≥ 0, а λ_n < 0, то форма неопределенна. Если исключить нулевую точку, то вдоль оси ξ₁ она положительная, вдоль же оси ξ_n - отрицательная.

Оказывается, что по виду матрицы ||А||, по знаку некоторых порождаемых ею определителей можно узнать, будут ли ее собственные числа все положительные, все отрицательные или среди них есть как положительные, так и

170

отрицательные. В этом заключается теорема Сильвестра¹.

Составим ряд главных миноров квадратичной формы (Ах, х):

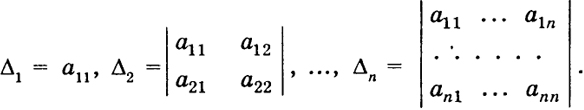
Согласно теореме Сильвестра, которую мы не доказываем, имеют место следующие утверждения:

1. Если Δ₁ > 0, Δ₂ > 0, ..., Δ_n > 0, то форма строго положительна (случай 1)).
2. Если Δ₁ < 0, Δ₂ > 0, Δ₃ < 0, ..., (-1)ⁿΔ_n > 0, то форма строго отрицательная (случай 2)).
3. Если Δ₁ > 0, Δ₂ > 0, ..., Δ_n > 0 или Δ₁ < 0, Δ₂ > 0, ..., (-1)ⁿΔ_n > 0
   и имеется у, при котором Δ_j = 0, то форма заведомо не строго определенна.
4. Во всех остальных случаях квадратическая форма неопределенна.

Замечание 1. Если R_n - комплексное пространство, a a_kl = a_lk - по-прежнему действительные числа, то рассуждения, приведенные выше, мало отличаются. Формула (4') теперь записывается так:

(x, Ax) =

n

∑

k=1

 x_k

n

∑

l=1

 a_klx_l =

n

∑

k=1

 

n

∑

l=1

 a_klx_kx_l.

Число (х, Ах) остается действительным, потому что

(x, Ax) =

n

∑

k=1

 

n

∑

l=1

 a_klx_kx_l =

n

∑

k=1

 

n

∑

l=1

 a_lkx_kx_l =

n

∑

k=1

 

n

∑

l=1

 a_klx_kx_l =
= (x, Ax)

171

Это показывает, что приведенные выше факты (формулы (4')-(10)) остаются неизменными, в частности числа λ₁, ..., λ_n и в случае комплексного R_n действительны. Теорема 1 полностью сохраняется для комплексного R_n. Формула (4") теперь имеет вид

(x, Ax) =

n

∑

s=1

 λ_s |(x, x^s)|²,

т. е. теперь уже квадраты чисел (х, x^s) надо заменить на квадраты их модулей. Формула (4’’’) теперь уже выглядит следующим образом:

n

∑

k=1

 

n

∑

l=1

 a_klx_kx_l =

n

∑

s=1

 λ_s|ξ_s|²,

а в остальном теорема 2 остается в силе.

Замечание 2. Отметим, что действительность собственных значений самосопряженного линейного оператора А и R_n (действительном или комплексном) можно доказать следующим образом. Пусть λ - собственное значение оператора А и x⁰ (|x⁰| = 1) - принадлежащий к нему собственный вектор. Так как Ах⁰ = λx⁰, то

λ = λ(x⁰, x⁰) = (λx⁰, x⁰) = (Ax⁰, x⁰) = (x⁰, Ax⁰) =
= (x⁰, λx⁰) = λ(x⁰, x⁰) = λ.

Ортогональность собственных векторов оператора, при надлежащих разным собственным значениям, тоже можно доказать непосредственно.

В самом деле,

Ах¹ = λ₁х¹, Ах² = λ₂х²

(|x¹| = 1, |x²| = 1, λ₁ ≠ λ₂),

тогда

172

λ₁(x¹, x²) = (λ₁x¹, x²) = (Ax¹, x²) = (x¹, Ax²) =
= (x¹, λ₂x²) = λ₂(x¹, x²) = λ₂(x¹, x²).

Так как λ₁ ≠ λ₂, то (x¹, x²) = 0.

173

---