Понятие прямой является первичным в геометрии. Из аксиом геометрии мы знаем, что через две точки проходит единственная прямая и через точку, лежащую на данной
69
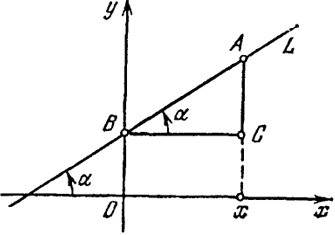
Рис. 12
прямой, можно провести единственную прямую, перпендикулярную данной.
В плоскости зададим прямоугольную систему координат х, у и прямую L, не параллельную оси у (рис. 12).
Из школьного курса мы знаем, что уравнение прямой L имеет вид
y = kx + l, (1)
где k = tgα и α - угол, образованный прямой L с положительным направлением оси х, а l - ордината точки пересечения L с осью у (l = ОВ).
Когда говорят, что уравнение (1) есть уравнение прямой L, этим хотят выразить, что L есть геометрическое место точек, координаты которых (х, у) удовлетворяют уравнению (1). Справедливость этого утверждения легко усмотреть из рис. 12. Точка А есть произвольная (текущая) точка прямой L, имеющая координаты (х, у) ВС = д:, АС = у - l и
k = tgα =
откуда следует (1). Обратно, равенство (1) эквивалентно равенству (1'), а последнее выражает, очевидно, тот факт, что точка (х, у) лежит на прямой L. На рис. 12 угол а острый. В случае тупого угла а можно провести подобные рассуждения.
70
Зададим уравнение
Ах + By + С = 0, (2)
где А, В, С - заданные числа и к тому же А и В одновременно не равны нулю.
Если В ≠ 0, то уравнение (2) можно записать в следующем виде:
y = -
х = -
(2')
или, полагая
k = -
,
i = -
в виде (1). Так как уравнения (2) и (2 ) эквивалентны -любая точка (х, у), удовлетворяющая одному из них, удовлетворяет и другому, - то равенство (2) при В ≠ 0 есть уравнение прямой, наклоненной к положительному направлению оси х под углом ос, тангенс которого равен -А/В (tgα = -А/В), и пересекающей ось у в точке, имеющей ординату -С/В (l = -С/В). При В = 0 уравнение (2) принимает вид
Ах + С = 0 (А ≠ 0!),
или
х = а (а = -С/А).
Это тоже уравнение прямой, но только параллельной оси у. Именно, это есть геометрическое место точек (х, у), абсциссы х которых равны одному и тому же числу а. На рис. 13 изображена такая прямая при а > 0.
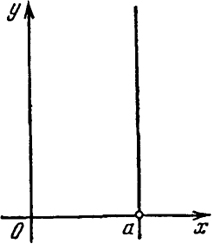
Рис. 13
Из сказанного следует, что уравнение (2), где А, В, С - заданные числа и при этом А и BOLDодновременно не равны нулю, есть уравнение некоторой прямой. При В ≠ 0 эта
71
прямая не параллельна оси у. В частности, при А = 0 она параллельна оси х (у = -С/В). В случае же, если В = 0, то она параллельна оси у. Отметим, что ось х имеет, очевидно, уравнение у = 0, а ось у имеет уравнение х = 0.
Уравнение (2) называется уравнением прямой в общем виде. Любая прямая, как угодно расположенная по отношению к системе координат, может быть описана уравнением вида (2) при подходящих постоянных числах А, В, С. Подчеркнем, что числа А и В в уравнении (2) прямой одновременно не равны нулю. Отметим, что число k в уравнении (1) называют угловым коэффициентом прямой.
Решим несколько важных задач.
Задача 1. Написать уравнение прямой с угловым коэффициентом, равным числу k, проходящей через заданную точку ( x0, y0).
Решение. Прямая с угловым коэффициентом k имеет вид
y = kx + l, (3)
где l может быть любым числом. Так как точка ( x0, z0) должна находиться на данной прямой, то должно выполняться равенство
yо = kх0 + l. (4)
Вычитая (4) из (3), получим искомое уравнение
y - y0 = k(x - x0) (5)
прямой, проходящей через точку (х0, x0) с угловым коэффициентом k.
Задача 2. Написать уравнение прямой, проходящей через заданные две точки (х1, y1) и (х2 у2). Предполагается, что эти точки разные.
Решение. Пусть х ≠ х2 Тогда, очевидно, искомая прямая не параллельна оси у и потому может быть записана в виде
72
y - y1 = k ( x - x1) (6)
где k - некоторое число. Уравнение (6) уже выражает, что прямая проходит через точку (х1, у1). Чтобы она проходила также через точку (x2, у2), надо чтобы выполнялось равенство
y2 - y1 = k ( x2 - x1)- (7)
Деля (6) на (7) (т. е. деля левую часть (6) на левую часть (7), а правую часть (6) на правую часть (7)), получим
=
(8)
Это и есть уравнение прямой, проходящей через точки ( x1, y1) и (х2, у2).
Замечание 1. Могло случиться, что у2 - y1 =0, тогда формально мы получили бы равенство
=
Несмотря на бессмысленность этого равенства, так пишут - считают удобным. Если освободиться от знаменателей, то получим верное равенство
y- y1= 0 ∙
= 0
или
y = y1 (9)
Случай x1 = х2 = с приводит к решению х = с.
Задача 3. Найти угол ω между прямыми
у = k1х + l1/,, у = k2x = 12.
Решение. Имеем k 1 = tgα, k2 = tgα2, где α1 α2 - соответственно углы, образованные данными прямыми с
73
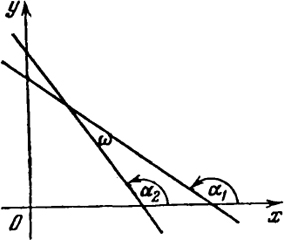
Рис. 14
положительным направлением оси х. Имеем (рис. 14)
tgω = tg(α1 - α2) =
=
(10)
и мы получили формулу угла между прямыми.
Случай 1 + k1k2 = 0 или
k1 ∙ k2= -l (11)
выражает условие перпендикулярности прямых. Условие параллельности прямых (tgω = 0), запишется так
k1 = k2 (12)
Зададим уравнение прямой в общем виде:
Ах + By + С = 0. (2)
При А ≠ 0, В ≠ 0, С ≠ 0 уравнение (2) можно записать в форме
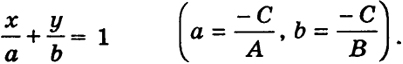 (13)
(13)
Уравнение (13) называется уравнением прямой в отрезках. Эта прямая пересекает ось x: (прямую у = 0) в точке ( а, 0) и ось у в точке (0, b).
74
Если прямая, удовлетворяющая уравнению (2), проходит через точку (х0, у0), то
Ах0 + Ву0 + С = 0. (14)
Вычитая (14) из (2), получим
А(х - х0) + В(у - y0) = 0. (15)
Уравнение (15) называется уравнением прямой, проходящей через точку (х0, у0).
Если ввести в рассмотрение векторы N = (А, В), ρ = (х, у), ρ0 = (х0, y0), то левую часть(15) можно рассматривать как скалярное произведение вектора N на вектор ρ - ρ0. Поэтому уравнение (15) в векторной форме имеет вид
N(ρ - ρ0) = 0. (15')
Вектор ρ - ρ0 принадлежит прямой L (рис. 15). Таким образом, из (15') видно, что вектор N = (А, В) ортогонален
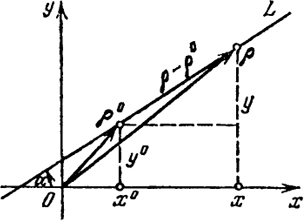
Рис. 15
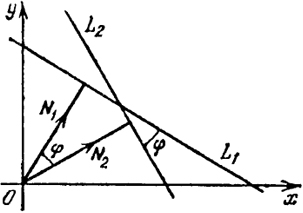
Рис. 16
(перпендикулярен) данной прямой, и тем самым мы выяснили геометрический смысл коэффициентов A и В. Рассмотрим две прямые
А1х + В1у + С1 = 0 ( L 1), (16)
А2х + В2у+ С2 = 0 ( L2). (17)
75
Так как векторы N1 = (А1, B1) и N2 = (A2, В2) перпендикулярны к прямым (16) и (17) соответственно, то угол φ между прямыми (16) и (17) равен углу между векторами N1и N2 (рис. 16). Угол φ можно вычислить по формуле
 (18)
(18)
Замечание 2. Если φ - угол между прямыми, то π - φ также является углом между этими прямыми. Число (18) может быть положительным и отрицательным. Одно из них соответствует углу ф, а другое - углу π - φ.
Из (18) получаем условие перпендикулярности L1 и L2
(φ =
, cos φ = 0):
А1А2 + В1В2 = 0. (19)
Если прямые L1 и L2 параллельны, то векторы N1и N2 коллинеарны и N1 = λN2, где λ - некоторое действительное число. Отсюда условие параллельности прямых выражается равенством
=
(20)
Пусть дана произвольная прямая L в прямоугольной системе координат (рис. 17), не проходящая через начало координат, и пусть а - вектор, выходящий из начала координат и перпендикулярный к прямой L с концом, лежащим на прямой. Вектор а полностью определяет прямую L (через конец вектора а проходит единственная прямая, перпендикулярная к нему).
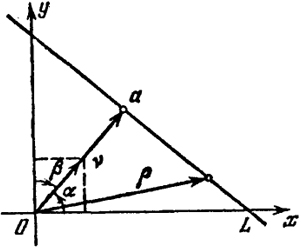
Рис. 17
76
Пусть р есть длина а (р = | а |), ν = (cos α, cos β) есть единичный вектор, направленный в ту же сторону, что и а. Здесь α, β - углы между а (или ν) и соответственно положительным направлением оси х и оси у; cos 2α + cos 2β = 1 (cos β = sin α). Обозначим через ρ = (х, у) радиус-вектор произвольной (текущей) точки прямой L. Проекция вектора ρ на единичный вектор ν, очевидно, равна p, т. е. скалярное произведение радиус-вектора произвольной точки ρ прямой L на вектор ν равно р:
(ρ, ν) = |v|npvp = р. (21)
Итак, мы получили векторное уравнение L, потому что, и обратно, если радиус-вектор точки удовлетворяет уравнению (21), то точка лежит на L (точка, не лежащая на L, имеет проекцию на ν, отличную от р).
Если прямая L проходит через начало координат, то ее уравнение можно записать тоже в виде (21), где ν - единичный перпендикулярный к ней вектор и р = 0.
В координатной форме уравнение (21) имеет вид
xcos α + ycos β = р (р ≥ 0) (21')
или
xcos α + ysin α = р (р ≥ 0). (21'')
Уравнение (21') (или (21'')) называется уравнением прямой в нормальном виде.
Если прямая L задана общим уравнением
Ах + By + С = 0,
то его можно привести к нормальному виду, умножив на число
М = ±1√A2+B2 , (22)
где надо выбрать знак, противоположный знаку С (р = -МС ≥ 0). Число М называется нормирующим множителем. Так как
77
( MA)2 + (MB)2 = 1,
то существует и притом единственный угол ос, удовлетворяющий неравенствам 0 ≤ α ≤ 2π, для которого
MA = cos α, MB = sin α. (23)
В результате мы получаем уравнение (21), где р = -МС ≥ ≥ 0. Отметим еще раз, что число р равно расстоянию от начала координат до прямой.
Задача 4. Найти расстояние d от точки до прямой L, определяемой уравнением
Ах + By + С = 0. (24)
Решение. Пусть
(ρ, ν) - р = 0 (25)
есть нормальное уравнение прямой (24). Таким образом, если С ≠ 0, то р (р > 0) есть длина вектора ОР→, опущенного из начала координат О на L (перпендикулярно к L), а ν - единичный вектор, направленный как ОР→ (р = | ОР→ | ν = ОР→/р (рис. 18)). Пусть р = (х, у) есть радиус-вектор произвольной точки L. Тогда, очевидно, чтобы найти расстояние от точки Q0, имеющей радиус-вектор ρ0 = ( x0, y0) до L, надо спроектировать вектор ρ - ρ0 на направление вектора ν и взять абсолютную величину проекции:
d = |npν (ρ - ρ0)| = |ρ - ρ0, ν)| = |(ρ, ν) - (ρ0, ν)| = |р - (ρ0, ν)) = |(ρ0, ν) - р|,
Мы получили формулу
d = |(ρ0, ν) - р|. (26)
Таким образом, чтобы получить расстояние d, надо привести уравнение (24) к нормальному виду, перенести р
78
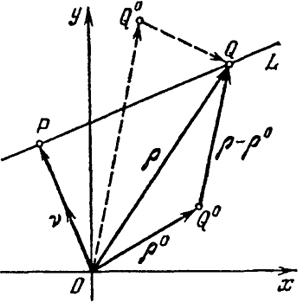
Рис. 18

Рис. 19
в левую часть, подставить в левую часть вместо х, у соответствующие координаты x0, y0точки Q0 и взять абсолютную величину полученного выражения.
На языке коэффициентов А, В, С равенство (26) выглядит так:
d = |Ax0 + By0 + C|/√A2 + B2. (26')
При С = 0 формула (26), а следовательно и (26'), остается тоже верной. В этом случае р = 0, ν - один из двух единичных векторов, перпендикулярных к L (рис. 19).
Теперь
d = |пpν (ρ - ρ0)| - |(ρ - ρ0, ν)| - |(ρ, ν) - (ρ0, ν)| = |(ρ0, ν)|
или
d = |Ах0 + Ву0|/√А2 + В2 ,
т. е. формула (26') верна при С = 0.
Замечание 3. Из рис. 18 видно, что: а) если начало О и точка Q0 находятся по одну сторону от L, то угол между ν и ρ - ρ0 острый и d = р - (ρ0, ν); б) если же О и Q0 находятся по разные стороны от L, то угол между ρ - ρ0 и ν тупой и d = (ρ0, ν) - р.
79
Задача 5. Найти расстояние от точки (1, 1) до прямой
2 x + √5 y - √5 = 0.
80
