Зададим произвольные точки x, у ∈ Rn и введем множество точек (векторов):
z = λ х + μ у (λ, μ ≥ 0, λ, + μ = 1), (1)
определяемых неотрицательными числами λ, μ, сумма которых равна 1. Имеем
z = (1 - μ) X + μ y = х + μ ( у - х) (0 ≤ μ ≤ 1) (2)
или
z = у + λ( х - у) (0 ≤ λ ≤ 1). (2')
Из равенства (2) видно, что в трехмерном пространстве точки z заполняют отрезок, соединяющий х и у.Ведь радиус-вектор z есть сумма вектора х и вектора μ( y - х), коллинеарного с у - х (рис. 11). Таким образом, множество точек (1) представляет собой отрезок
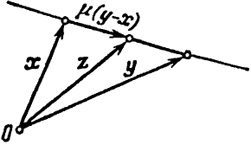
Рис. 11
67
[х, у] в R3, соединяющий точки х и у. При μ = 0 z = x при μ = 1 z = у, для любого μ > 0 (0 ≤ μ ≤ 1) z есть произвольная точка [ x, у].
По определению отрезком [ x, у], соединяющим точки х, у ∈ Rn, называется множество всех точек z вида (1). Справедлива
Теорема 1. Точка
z = λ x + μ у (λ, μ ≥ 0, λ + μ = 1)
делит отрезок [ х, у], соединяющий точки х, у ∈ Rn на отрезки с длинами, находящимися в отношении μ : λ.
Доказательство. Из (2) следует, что z - х = μ( y - х), и потому расстояние между точками х и z равно
| z - х| = μ| y - x | (3)
Далее, из (2') z - у = λ( x - у), и потому расстояние между точками z и у равно
| z - у| = λ| x - у |. (4)
Из (3) и (4) следует
| z - х| ∶ | z - у| = β ∶ λ,
что и требовалось доказать.
Задача. Требуется найти на отрезке [ х, у], соединяющем точки х, у ∈ Rn, точку z, делящую этот отрезок в отношении р ∶ q (р > 0, q > 0).
Решение. Возьмем числа
λ =
, μ =
(
р ∁ 0,
q ∁ 0,
p + q > 0).
Они удовлетворяют свойствам λ, μ ≥ 0, λ + μ = 1, μ/λ = p/q. Поэтому на основании теоремы 1 искомая точка
z = λ x + μ y =
(5)
68
Ее координаты z = (z1 ..., zn) выражаются через координаты х = ( x1 ..., хп), у = ( y 1, ..., уп) при помощи равенств
zj =
(
j =1, …,
n). (5')
В частности, середина отрезка получается при р = q = 1, т. е. λ = μ = 1/2.
Отметим, что, как доказывается в механике, точка z, определяемая равенством (5) или (5'), есть центр тяжести системы точек х и у, в которых сконцентрированы массы соответственно q. и р.
Отметим, что в R3 множество точек
z = λ х + μ y, λ + μ = 1,
где λ, и μ любого знака представляет собой прямую, проходящую через точки х и у. Это видно из равенства (2').
В пространстве же Rn (n > 3) это множество называют прямой по определению.
Пример 1. Найти координаты центра тяжести системы материальных точек xk = (х1 k, х2 k, x3 k) соответственно с массамиk (k = 1,..., М). Применяя формулы (5') для точек х1, х2, найдем центр тяжести z 1точек х 1и х 2.Затем находим центр тяжести z 2точек z 1и х 3соответственно с массами р1 + р2 и р3.Продолжая этот процесс на (М - 1)-м шаге, получаем
 (j = 1, 2, 3).
(j = 1, 2, 3).
69
