§ 3. Матрицы

Таблица чисел a_ij (действительных или комплексных) вида

(1)

состоящая из т строк и п столбцов, называется матрицей. Числа ctl7 называются ее элементами. Это прямоугольная матрица. При т = п она называется квадратной матрицей n-го порядка.

Если задана вторая матрица В = ||β _ij || с элементами β _ij, тоже состоящая из т строк и п столбцов, то она считается равной матрице А тогда и только тогда, когда соответствующие элементы обеих матриц равны (α _ij = β _ij). В этом случае пишут А = В. Матрица ||α _ij|| не есть число - это таблица. Однако для квадратной матрицы можно рассматривать число |α _ij | - определитель, порожденный этой матрицей.

Пусть k - натуральное число, не превышающее т и п (k < т, п). Зачеркнем в таблице (1) какие-либо k столбцов и k строк. Элементы α _ij, находящиеся на пересечении

22

зачеркнутых столбцов и строк, образуют квадратную матрицу, которая порождает определитель k-ro порядка. Полученный определитель называется определителем k-го порядка, порожденным матрицей А.

Рангом матрицы А называется наибольшее натуральное число k, для которого существует не равный нулю определитель k-то порядка, порождаемый матрицей А (см. § 4).

Если в матрице А сделать ее строки столбцами с тем же самым номером, то получим матрицу

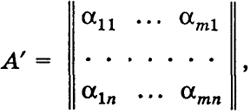(2)

называемую транспонированной к А матрицей.

Если в матрице А ее элементы α _kl заменить на им комплексно сопряженные, то получим матрицу

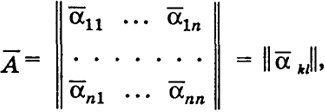
называемую комплексно сопряженной с А матрицей.

Далее матрица

называется сопряженной с А матрицей.

Если А - действительная матрица, т. е. имеющая действительные элементы (α _kl = α _kl), то, очевидно,

А = А, А' = А^*

23

Матрицы одного и того же размера, т. е. состоящие из одинакового числа строк и столбцов, можно складывать. Суммой двух таких матриц А = |α _ij || и В = ||β _ij | называется матрица С = ||γ _ij |, элементы которой равны сумме соответствующих элементов матриц А и В: γ _ij = α _ij + β _ij.Символически этот факт будем записывать так:

А + В = С.

Легко видеть, что

А + В = В + А,
(А + В) + С = А + (В + С).

Произведением числа γ на матрицу А (или произведением матрицы А на число γ) будем называть матрицу, элементы которой равны произведению числа γ на соответствующие элементы матрицы А. Таким образом, γА = Aγ.

Пример.Пусть

Найти матрицу γА + μВ.

На основании определения суммы матриц и умножения матрицы на число имеем

24