28.1. Введение. Линейное программирование - это раздел математики, изучающий методы нахождения максимальных или минимальных значений линейной однородной формы - линейной функции
f(x1, …, xn) =
ckxk (1)
в некоторой области G n-мерного пространства Rn = {-∞ < x < ∞, i = 1, ..., n}, где сk - постоянные числа, не все равные нулю.
Ясно, что если G = Rn, то линейная функция (1) не имеет наибольшего и наименьшего значений: supf = +∞, inff = -∞.
Однако если мы будем рассматривать ограниченную замкнутую область G, то линейная функция f (непрерывная на Rn, a следовательно, и на G) достигает своих максимальных и минимальных значений на G. Так как
=
ci (
i = 1, …,
n ≡
1, n)
и ci одновременно не равны нулю, то линейная функция f не имеет стационарных точек. Поэтому наибольшее и наименьшее значения эта функция достигает только на границе ∂G.
Так как maxf = -min(-f), то в дальнейшем мы будем говорить только о минимуме линейной функции f на G.
28.2. Транспортная задача. Характерной задачей, приводящей к указанной выше проблеме (нахождения минимума или максимума линейной функции),
241
является транспортная задача. Требуется наиболее экономно, в смысле транспортных затрат, перевезти потребителям заказанную ими на данных предприятиях продукцию. Характер продукции в данном случае не имеет значения. Важно, что речь идет об однотипной продукции.
Итак, пусть имеются предприятия (производители) B1, ..., Вs, выпустившие продукцию в количестве соответственно b1, ..., bs тонн. Эту продукцию надо доставить потребителям А1, ..., As в количествах а1, ..., as тонн соответственно, т. е. аρ - количество продукции, заказанное потребителем Аρ.
Таким образом, надо считать, что
bq =
ap,
т. е. вся произведенная продукция распределена между предприятиями. Стоимость перевозки тонны продукции от Bq к Ар обозначим через сqp. Пусть количество продукции, доставленной из Bq в Аp , будет хqp. Тогда стоимость перевозки продукции будет
S =
bq =
ap
Требуется так составить план перевозок, чтобы сумма транспортных расходов S была минимальной.
Таким образом, мы пришли к следующей математической задаче.
Дана линейная функция
S =
cqpxqp (2)
Требуется найти ее минимум при ограничениях
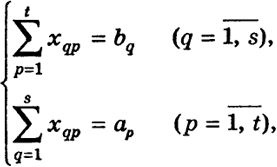 (3)
(3)
т. е. сумма продукции, полученной потребителями А1, ..., At от производителя Вq , равна продукции bq
242
выработанной этим предприятием, а сумма продукции, полученной потребителем Аp от всех производителей В1, ..., Bs, равна потребности ар этого потребителя.
По характеру задачи также ясно, что хqp ≥ 0.
Таким образом, среди неотрицательных решений {хqp} системы (3) необходимо выбрать такое, при котором S достигает наименьшего значения (минимизируется).
28.3. Общая задача линейного программирования. В общем случае задачу линейного программирования можно сформулировать следующим образом: даны система линейных уравнений
ajkxk +
bj = 0 (
j = 1, …,
m ≡
1, m) (4)
(где можно считать, что bj ≥ 0, изменяя, если нужно, знак в соответствующем уравнении (4)) и линейная функция
f =
ckxk. (1)
Требуется среди неотрицательных решений системы (4) х = (x1, ..., xn), хj ≥ 0, найти такое решение, для которого линейная функция f принимает наименьшее значение.
Уравнения (4) обычно называют ограничениями данной задачи. Конечно, требование, чтобы хj ≥ 0 (j = 1, n), тоже является ограничением, но оно присутствует во всех задачах подобного типа и его не принято называть ограничением. Любое неотрицательное решение системы (4) будем называть допустимым, а решение, реализующее минимум, - оптимальным.
Отметим, что уравнения системы (4) с геометрической точки зрения представляют плоскости в Rn. Чтобы задача о минимуме f была содержательной, необходимо, чтобы число т ограничений типа равенств было меньше п.
Например, при п = 2 наличие двух ограничений означает, что неотрицательное решение системы должно быть точкой (x0, y0) пересечения прямых, представляющих уравнения системы. Тогда задача о нахождении min/ сводится к вычислению f в этой точке. Если прямые параллельны, то задача теряет смысл. Если ограничений больше двух,
243
то система или несовместна, или же все прямые принадлежат одному пучку:
А(х - x0) + В(у - у0) = 0.
В этом случае минимум f также равен f(x0, y0). В ряде практических задач (например, в задаче о диете) ограничения носят вид неравенств
bj +
ajkxk ≥ 0 (
j =
1, m,
xk ≥ 0,
k =
1, n). (5)
Однако от одного типа ограничений легко перейти к другому. В самом деле, если ограничения носят характер неравенств (5), то вводим новые добавочные неизвестные xn+1, ..., xn+m с помощью уравнений
xn+j = bj +
ajkxk (
j =
1, m)
Тогда неравенства (5) равносильны условию xn+j ≥ 0 (j = 1, m ), xk ≥ 0 (k = 1, п ), и мы пришли к ограничениям типа равенств (4), хотя и с большим числом переменных. Обратно, пусть имеют место ограничения типа равенств (4). Тогда, решая эту систему (например, методом исключения неизвестных), мы после некоторого числа шагов или убедимся, что система несовместна, или же разрешим систему (4) относительно некоторых неизвестных:
x1 = α1,r+1xr+1 + … + α1,nxn + β1,
..................
xr = αr,r+1xr+1 + … + αr,nxn + βr, (6)
Здесь r - ранг матрицы коэффициентов системы (4).
Подставляя эти выражения x1, ..., хr в функцию f, получаем
f = c
+
cxr+1 + … +
cxn.
После этого исходная задача может быть сформулирована следующим образом. Даны система
244
α1,r+1xr+1 + … + α1,nxn + β1 ≥ 0,
..........
αr,r+1xr+1 + … + αr,nxn + βr ≥ 0 (7)
r линейных неравенств с п = r неизвестными х1, ... хп и линейная функция
f= с + с + ... + cxn. (8)
Требуется среди всех неотрицательных решений системы (7) найти такое, которое минимизирует f.
Эта задача эквивалентна исходной. В самом деле, если мы нашли решение задачи (7), (8) x, ..., х, то, находя по формулам (6) неотрицательные значения х, ..., х, мы получим систему чисел
x, …, x, x, …, x,
которая служит решением задачи (1), (4).
Таким образом, задачу линейного программирования можно ставить с ограничениями типа неравенств. Из такой постановки видно, что область G, в которой мы ищем минимум f, представляет собой "многогранник" в неотрицательном угле Rn (т. е. когда xk ≥ 0, k = 1, n), а ее граница ∂G состоит из "плоских граней", находящихся в плоскостях пространства Rn:
ajkxk +
bj = 0. (9)
Множество G ⊂ Rn называется выпуклым, если ∀ x, у ∈ G αх + βу ∈ G, α + β = 1, α, β ≥ 0.
Из системы неравенств (7) ясно, что "многогранник" G выпуклый и G находится по одну сторону от любой из своих граней.
Слово "многогранник" мы пишем в кавычках, так как могут быть случаи, когда этот "многогранник" будет неограниченной частью неотрицательного угла Rn.
Например, при п = 2 и при тех ограничениях типа неравенств "многоугольник" G может быть неограниченным в первой четверти R2. На рис. 54 G - заштрихованная часть.
245

Рис. 54
В дальнейшем кавычки у слова "многогранник" мы будем опускать.
При нахождении минимума линейной функции f на замкнутой области G = Gn мы последовательно будем переходить на плоские грани Gn меньшей размерности. Отметим, что граница ∂Gn n-мерного многогранника состоит из нескольких (п - 1)-мерных многогранников. Если Gn - ограниченный замкнутый многогранник, то линейная функция f достигает минимума в некоторой точке границы ∂Gn. При рассмотрении линейной функции f на этом новом многограннике меньшего числа измерений она снова будет линейной функцией, но от меньшего числа переменных и, следовательно, будет достигать минимума на границе ∂Gn-1 которая состоит из (п - 2)-мерных многогранников. Продолжая этот процесс, мы придем к случаю, когда линейная функция рассматривается на одномерной грани (ребре Gn), границей которой являются точки (вершины многогранника Gn).
Таким образом ясно, что если Gn - ограниченный замкнутый многогранник, то линейная функция достигает минимума в некоторой вершине Gn.
Если минимальное значение достигается в двух вершинах, конусах ребра, соединяющего эти точки, то в этой ситуации существует бесконечное множество точек, в которых линейная функция достигает минимума.
246
Замечание 1. Если функция f =
ckxk +
В, где
В - постоянное число, то мы исследуем сначала линейную форму φ =
f -
В, и если min φ = φ
0, то min
f = φ
0 +
В.
Из приведенных соображений вытекает следующий геометрический метод решения поставленной задачи о минимуме линейной формы f.
Рассмотрим плоскости уровня функции f:
C =
ckxk (-∞ <
C < ∞). (10)
Уравнение (10) при различных С в пространстве Rn изображает семейство параллельных плоскостей (см. § 27). Будем непрерывно и монотонно изменять С от -∞ до +∞. Тогда плоскость (10) будет передвигаться в Rn в направлении вектора (с1, ..., сп), который, как мы знаем, перпендикулярен плоскости (10). Очевидно, что если сп > 0, то плоскость (10) поднимается вверх относительно оси хп при изменении С от -∞ до +∞; если же сп < 0, то плоскость (10) опускается вниз относительно оси хп. При сn = 0 плоскость (10) движется вправо или влево относительно оси хn-1 в зависимости от знака числа сn-1 (сn-1 ≠ 0). Если сп > 0 и при всех С < С*, где С* - некоторое действительное число, плоскость (10) пересекает область G, то inff = -∞.
Если же этого нет, то при некотором С = С0 плоскость (10), двигаясь в направлении вектора (с1, ..., сп), впервые встретит замкнутую область G в некоторой точке (х, …, х). Тогда в этой точке встречи функция f и достигает минимума.
На рис. 54 при п = 2 прямая уровня при возрастании С поднимается и при С = С0 впервые встречает замкнутый многоугольник G в точке (х, х). Значит, min f= f(x, x).
Если грань многогранника G, проходящая через точку первой встречи G с плоскостью уровня, параллельна плоскости (10), то линейная функция f достигает минимума в любой точке этой грани.
Этот геометрический метод решения поставленной задачи эффективен лишь при п = 2, т. е. когда плоскости
247
(10) - прямые и G - многоугольник, ограниченный или нет. При п = 3 взаимное расположение плоскостей и многоугольника G трудноуловимо, а при п = 4 мы просто не можем прибегнуть к наглядным графическим изображениям.
Пример 1. Найти минимум функции f(x, у)=3 - х - у (х ≥ 0, у ≥ 0) при ограничениях (рис. 55)

Ясно, что область G есть треугольник с вершинами в точках М = (2, 0), N = (1, 2), Р = (0, 1). Прямая уровня функции f:
3 - х - у = С,
при возрастании С от -∞ до +∞ опускается относительно оси у (коэффициент при у отрицателен); ее первая точка встречи с G есть вершина N. Значение функции f в этой точке равно нулю (С = С0 = 0). Итак, решение задачи есть х = 1, у = 2, f = 0.
В данном случае можно было бы просто вычислить значение f в точках М, N, Р и взять наименьшее: f(М) = f(2, 0) = 1, f(N) = f(1, 2) = 0, f(P) = f(0, 1) = 2, т. е. min f = f(N) = 0.

Рис. 55
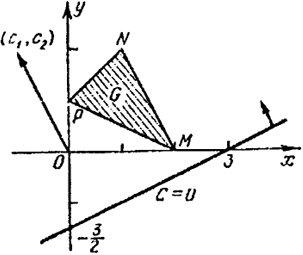
Рис. 56
248
Пример 2. Найти минимум функции f = 3 - х + 2у при тех же ограничениях, что и в примере 1.
В данном случае прямая уровня функции
3 - х + 2у = С
при возрастании С от -∞ до +∞ поднимается (рис. 56) вверх относительно оси у (с2 = 2 > 0) и ее первая точка встречи с областью G есть вершина М = (2, 0). Значение функции f в этой точке равно 1 (С = С0 = 1). Здесь тоже проще всего взять наименьшее среди чисел f(M) = 1, f(N) = 6, f(Р) = 5.
Пример 3. Найти минимум функции f = -х при ограничениях
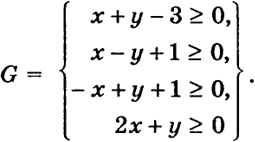
Ясно, что последнее ограничение несущественно, оно перекрывается условием х ≥ 0, у ≥ 0.
Область G неограничена и представляет собой полосу (рис. 57) между прямыми х - у + 1 = 0, -х + у + 1 = 0 и правее прямой х + у - 3 = 0, которая пересекает эти прямые в точках N = (1, 2), М = (2, 1).
При х → +∞ функция f(x, у) = -х → -∞, (х, у) ∈ G. Поэтому линейная функция f не имеет наименьшего значения (inff = -∞).
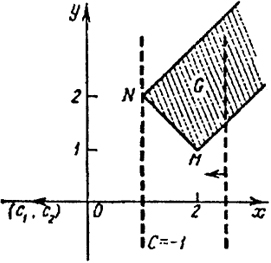
Рис. 57
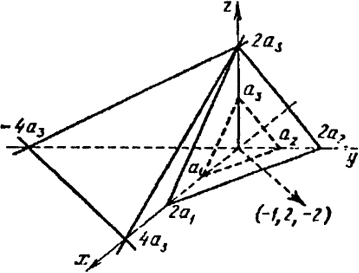
Рис. 58
249
В данном примере прямая уровня -х = С при возрастании С от -∞ до +∞ движется влево (с1 = -1 < 0) и при всяком С < -1 пересекает G, значит, inff = -∞.
Пример 4. Найти минимум функции f = 4 - x + y - 2z при ограничениях

где а1 а2, а3 - положительные числа.
Ясно, что область G (рис. 58) есть часть пространства R3, находящаяся в первом октанте (х ≥ 0, у ≥ 0, z ≥ 0) между плоскостями
+
+
= 1,
+
+
= 1.
В данном случае многогранник G имеет шесть известных вершин
(а1, 0, 0), (2a1, 0, 0), (0, а2, 0), (0, 2а2, 0),
(0, 0, а3), (0, 0, 2а3).
Поэтому, вычисляя функцию f в этих точках, легко находим ее минимум и максимум:
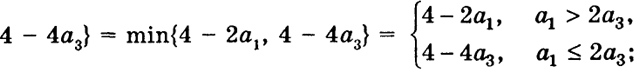
28.4. Векторно-матричная форма задачи линейного программирования. Задачу линейного программирования можно сформулировать также в векторно-матричной форме. Пусть с = (с1, ..., сn), х = (х1, ..., хп), 0 = (0, ..., 0) - векторы пространства Rn; b = (b1, ..., bm) - вектор из пространства Rm;
250
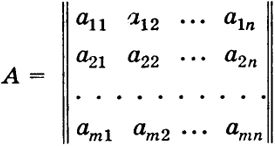
- матрица размера п × т, составленная из коэффициентов системы ограничений (4). Линейная функция f(x) =
ckxk =
сх есть скалярное произведение векторов
с и
х.
Поэтому общую задачу линейного программирования можно записать в следующем виде: требуется минимизировать скалярное произведение сх при условии х ≥ 0 и Ах + b = 0.
Примем столбцы матрицы А за векторы из Rm:
P1 = (а11, а12, ..., am1), ..., Рп = (a1n, а2n, ..., атп).
Тогда легко получаем, что
Ах = (а11х1 + ... + a1nxn, ..., am1x1 + ... + атпхп) =
= (а11х1, a21x1, ..., am1X1) + ... + (a1nxn, ..., атпхп) =
= Р1x1 + Р2х2 + ... + Рnxn.
Поэтому систему ограничений можно записать в виде
Pjxj = -
b.
Если ранг А = m, то среди векторов Р1, ..., Рп имеется т линейно независимых, которые можно принять за базис в пространстве Rm (см. § 16). Следовательно, любой вектор (-b) ∈ Rn может быть разложен по элементам этого базиса. Нам необходимо выбрать такой базис, чтобы вектор (-b) разлагался по векторам этого базиса с неотрицательными коэффициентами x1, x2, ..., хп.
Различных m-мерных базисов (m < n) из векторов Р1 ..., Рn конечное число. Среди них могут быть базисы, по элементам которых вектор (-b) разлагается с неотрицательными коэффициентами. Тогда минимум скалярного произведения (линейной функции) достигается на
251
конечном множестве точек x = (x1, ..., хп) ∈ Rn, где хj - коэффициенты разложения вектора (-b) по элементам некоторых базисов.
Если базисов указанного типа нет (вектор (-b) не разлагается по элементам базисов с неотрицательными коэффициентами), то задача линейного программирования не имеет решения (неразрешима).
Таким образом, задача состоит в том, как найти базис
(Pk, …, Pkm)
так, чтобы
-b =
xkjPkm,
xkj ≥ 0,
и
minf =
cx =
ckjxkj.
28.5. Симплекс-метод. Реальные задачи линейного программирования содержат, как правило, большое число ограничений и неизвестных. Поэтому естественно, что решение таких задач связано с большим объемом вычислений. Это затруднение преодолевается с помощью быстродействующих электронно-вычислительных машин (ЭВМ). Для каждой задачи разрабатываются алгоритм и программа, и затем ЭВМ в короткий срок дает решение поставленной задачи.
Существуют и другие общие методы, позволяющие найти решение любой задачи линейного программирования в обозримое число шагов.
Таким является симплекс-метод. Опишем идею этого метода.
Пусть надо найти минимум линейной функции
f(x) = c
+
cxj (11)
среди значений xj ≥ 0 (j = 1, ..., п), удовлетворяющих равенствам
252
axj +
b = 0 (
k = 1, …,
m;
m <
n). (4)
Неотрицательные решения системы (4) xj ≥ 0 (j = 1, n) мы условимся называть допустимыми, а точку x = (x1, ..., xn) - допустимой точкой. Покажем, как эту задачу можно решить, применяя симплекс-метод.
Пусть ранг матрицы А' = (а) равен r ≤ т(r - ранг А')-Будем считать, что система (4) разрешима относительно
xk = bk -
akjxj (
k =
1, r) , (12)
и числа bk неотрицательны (bk ≥ 0, k = 1, r).
В этом случае говорят, что переменные х1 ..., xr образуют базис - базис В = {х1, ..., хr}. Остальные переменные называются свободными или небазисными. Следует обратить внимание, что здесь понятие базиса не совпадает с понятием базиса из § 16.
Вопрос о возможности перехода от системы (4) к системе (12) будет рассмотрен ниже в п. 28.8.
Системы (4) и (12) равносильны, поэтому допустимая точка x системы (4) есть допустимая точка системы (12), и обратно.
Очевидно, точка b = (b1, ..., br, 0, ..., 0) допустимая, ее называют базисным решением, отвечающим базису В. Будем писать f(b) = fB. В силу равенств (12) функцию f можно записать в виде линейной функции от переменных xj (j = r + 1, ..., n):
f(x) = c0 -
cjxj. (13)
Очевидно, что fB = с0 = с
+
cbj.
Первый этап симплекс-метода связан с рассмотрением функции f, определяемой равенством (13), и системы ограничений в виде равенств (12).
253
Рассмотрим четыре возможных случая I, II, III+, III0.
Случай I. Пусть cj ≤ 0 для всех j = r + 1, ..., п. Тогда минимум f, определяемой равенством (13), относительно всех хj > 0, j = 1, ..., n, будет равен с0:
f(
x) =
с0.
Этот минимум остается тем же для допустимых x1, ..., хп. Этим задача на минимум решена.
Случай II. Пусть для некоторого j0 cj0 > 0 и все коэффициенты akj0 матрицы А = (akj) неположительны:
akj0 ≤ 0 (k = 1, ..., r).
Тогда при любом xj0 ≥ 0 (r + 1 ≤ j0 ≤ п) точка
x0 = (х1, ..., хr, 0, ..., 0, xj0 , 0, ..., 0). (14)
где xk (k = 1, ..., r) вычисляются по формулам (12), будет допустимой, и если ее подставить в f, то получим f = с0 - Cj0xj0 → -∞ при xj0 → +∞. Поэтому
f(
x) = -∞,
и нашу задачу о минимуме можно считать решенной.
Случай III. Пусть для некоторого j0 коэффициент сj0 функции f положительный (cj0 > 0) и имеются положительные коэффициенты akj0 в j0-м столбце матрицы А:
akj0 > 0 (k ∈ е), (15)
где е - множество индексов k, для которых выполняется неравенство (15).
Пусть
=
= δ ≥ 0 (1 ≤
k0 ≥
r,
k0 ∈
е). (16)
254
Элемент ak0j0 называют разрешающим элементом.
Рассмотрим отдельно случаи δ > 0 и δ = 0, которые будем обозначать через III+ и III0 соответственно.
Случай III+. Точка (14) для значений xj0 , удовлетворяющих неравенствам 0 ≤ хj0 ≤ δ (δ > 0), допустимая. В самом деле, в силу (12) при k ∈ e непосредственно видно, что
xk = bk - akj0xj0 ≥ 0 (akj0 ≤ 0),
а при k ∈ e в силу соотношений (15), (16) имеем
xk = bk - akj0xj0 ≥ bk - akj0δ =
= bk - akj0
≥
bk -
akj0 =
bk -
bk = 0.
Если xj0 непрерывно возрастает от 0 до δ, то все xk > 0 (k = 1, ..., r), a xk0 = xk0 - ak0j0xj0 к тому же непрерывно убывает от bk0 до 0. При дальнейшем возрастании xj0 переменная xk0 становится отрицательной и точка (14) перестает быть допустимой.
Функция
f(x0) = c0 - cj0xj0
при возрастании xj0 от 0 до δ убывает от f(b) = с0 до f(b1)= с0 - cj0δ, где
b1 = (b1 - а1j0 δ, ..., br - arj0 δ, 0, ..., 0, δ, 0, ..., 0) (17)
и δ стоит на j0-м месте.
Таким образом,
c0 = f(b) > f(b1) = с0 - сj0δ.
Отметим, что координата хk0 (k0 ∈ е) в (17) равна нулю:
255
xk0 = bk0 - ak0j0δ = bk0 - ak0j0
= 0.
Так как аk0j0 > 0, то k0-e уравнение системы (12) можно решить относительно xj0:
xj0 =
-
-
xj (18)
Мы выразили xj0 через xk0 и остальные переменные xj (j ≠ j0, j ≥ r + 1). Можно выразить через эти переменные также любую переменную xk (k ≠ k0, 1 ≤ k ≤ r), если подставить выражение (18) вместо xj0 в равенства (12), соответствующие любым k ≠ k0.
Итак, в случае III+ удается решить систему (12) относительно переменных
x1, …, xk0-1, xj0, xk0+1, …, xr. (19)
Условно запишем соответствующую систему равенств так:
xk = b -
axj (
k = 1, …,
r), (20)
хотя на самом деле в этих равенствах только переменные x1 (i ≠ k0, j0) остались прежними, а остальные переменные хk0 и xj0 поменялись местами.
Покажем, что свободные члены
b ≥ 0 (k = 1, ..., r). (21)
В самом деле, если k ∈ е, то (akj0 > 0)
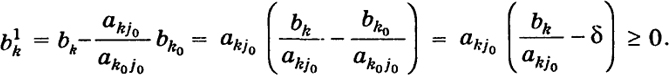
256
Если же k ∈ е (аkj0 ≤ 0), то
b = bk -
bk0 =
bk +
bk0 =
bk + |
akj0|δ ≥ 0
и неравенства (21) доказаны.
Итак, переменные x1, ..., хr в системе (20) образуют базис - базис В1 (см. также (19)).
Для базисного решения b1 = (b
, ...,
b, 0, ..., 0)
fB1 = f(b1) = с0 - сj0δ < с0 = f(b) = fB (cj0 > 0).
Базис B1 отличен от базиса B, и для него можно начать второй этап рассуждений (случай I, II, III). Таким образом, случай III+ рассмотрен.
Случай III0. Пусть сj0 > 0, аkj0 > 0 для k ∈ е, δ = 0. В этом случае bk0 = 0 (см. (16)) и равенство с номером k0 в (12) имеет вид
xk0 = -
ak0jxj. (22)
Если в равенстве (22) все коэффициенты ak0,r+1, ..., ak0,n положительные, то система (12) имеет единственное допустимое решение хj = 0, j = r + 1, ..., n; xk = bk ≥ 0 (k = 1, ..., r). Значение функции f на этом базисном решении будет: f = с0. Задача на минимум функции f в этом случае решена.
Допустим, что в (22) имеются коэффициенты аk0j ≤ 0 для некоторого значения j (j ≠ j0). Тогда, как и в случае III+, переходим к новому базису В1 (вводим в базис переменную xj0 и выводим из него хk0, ak0j0 - разрешающий элемент). Отметим, что в этом случае значение fB= fB1 (bk0 = 0).
257
Итак, рассматривая базис В, мы либо решим нашу задачу на минимум, либо придем к новому базису В1 (B1 ≠ В). К базису В1 снова применяем наш метод - это приведет к решению задачи либо к новому базису В2 (В2 ≠ B1). Продолжая этот процесс, получим цепочку базисов
В0, B1, B2, ... (В0 = В). (23)
Если для некоторого s будет иметь место случай I или II, то цепочка на этом s оборвется и задача будет решена. Иначе от базиса Вs переходим к базису Вs+1.
Однако может случиться цикл. Он заключается в том, что хотя каждый последующий базис цепочки и отличается от предыдущего, но для некоторых s и l (l > 1) будет происходить совпадение базисов: Вs = Bs+1.
Разберемся, что здесь происходит. Для базиса Вs+l-1 произошел случай III0, т. е. оказалось, что существует j0 (r + 1 ≤ j0 < п) и такое k0 (1 ≤ k0 ≤ r), что
Cj0 > 0, ak0j0 > 0 bk0 = 0 (δ = 0), (24)
и это привело к базису Bs (Bs+1 = Bs).
Но пара чисел (k0, j0), вообще говоря, неединственна, и какая-то другая пара (k
,
j0), для которой выполняются свойства (24), может привести к базису, отличному от базиса
Bs. Это на самом деле и имеет место, как учит теория (см. ниже теорему 1 и замечания к ней).
Таким образом, если для некоторых s и l случится цикл, то его можно устранить. В этом случае для базиса Вs+l-1 надо перебрать всевозможные пары (k0, j0), обладающие свойствами (24). Каждая такая пара приводит к некоторому базису. Среди них есть отличный от базисов В0, B1, ..., Bs+l-1.
28.6. Устранение цикла. На практике циклы бывают очень редко. Все же объясним, как их можно "разорвать" (устранить).
Отметим теорему, доказательство которой будет намечено в п. 28.7.
258
Теорема 1. От любого базиса В существует путь, ведущий к решению задачи на минимум, т. е. существует цепочка базисов, получаемых симплекс-методом, приводящая к минимуму (или к -∞).
Итак, пусть имеем цикл
Bs, BS+1, …, Bs+1 (Bs+1 = Bs)
Тогда, очевидно,
fBs = fBs+1 = … = fBs+l
Пусть s0 - наименьшее неотрицательное целое число, для которого
fBs0 = fBs+1 = … = fBs0+l
(fBs0-1 > fBs0, s0 ≤ s, Bs0 = Bs0+l)
Очевидно, для базисов
Bs0, Bs0+1, …, Bs0+l (25)
имеет место случай III0. Переход от любого из этих базисов Bs (s0 ≤ s ≤ s0 + l) к последующему совершается посредством разрешающего элемента аk0j0 . Но базису Bs может соответствовать и другой разрешающий элемент, который переводит Bs в базис В, отличный от Bs+l (В ≠ Вs+1).
Может случиться, что для любого s (s = s0, ..., s0 + l) базис B содержится в цепочке (25). Тогда все базисы (25) решают задачу на минимум, т. е. fBs0 = fBs0+1 = ... = fBs0+l = minf. Ведь по теореме 1 существует путь, ведущий от Bs0 к минимуму. Но в данном случае все пути от Вs0 ведут к базисам цепочки (25).
Однако может случиться, что для некоторого s разрешающий элемент базиса Bs переводит Вs в базис Bs+1, не входящий в цепочку (25). Тогда мы получим новую цепочку
Bs0, Bs0+1, …, Bs, B (26)
259
с новым последним базисом B, который подлежит исследованию симплекс-методом.
Но указанных значений s может оказаться и много. Одна из цепочек может и не привести к нужному результату. Необходимо произвести перебор всех цепочек. Отметим, что сам перебор цепочек становится громоздким.
Бели произошел цикл, то можно порекомендовать специальный метод выбора разрешающего элемента. Этот метод связан с дополнительными вычислениями, но зато последовательное его применение необходимо приводит к решению задачи без зацикливания (без образования циклов).
28.7. Выбор разрешающего элемента. Симплекс-таблицы. Условимся вектор Q = (q0, q1 ..., qn) называть положительным (отрицательным) и писать Q > 0 = (0, ..., 0) (Q < 0), если его первая не равная нулю компонента положительная (отрицательная).
Будем говорить, что вектор Q меньше вектора D = (d0, d1, ..., dn) или вектор D больше вектора Q, и писать Q < D или D > Q, если D - Q = (d0 - q0, ..., dn - qn) > 0.
Замечание 2. Целесообразность приведенных определений >, < для векторов Q можно подтвердить следующими соображениями.
Каждому вектору Q = (q0, ..., qn) поставим в соответствие многочлен от переменной t вида Q(t) = q0 + q1t + ... + qntn, который является непрерывной функцией и Q(0) = q0. Если q0 > 0, то найдется окрестность нуля такая, что для всех t из этой окрестности Q(t) > 0. Если же q0 = … = qk = 0 и qk+1 > 0, то
Q(t) = tk+1[qk+1 + qk+2t + ... + qntn-k+1].
Многочлен в квадратных скобках больше нуля (qk+l > 0) в некоторой окрестности нуля. Далее tk+l > 0 для t > 0. Значит, Q(t) > 0 для всех 0 < t < θ, где θ - некоторое положительное число.
Таким образом, если вектор Q > 0, то соответствующий многочлен Q(t) > 0 для 0 < t < θ при некотором θ > 0.
Вернемся теперь к системе ограничений (12), которую мы запишем в форме
260
Таблица 1

261
xk +
akjxj =
bk (
bk ≥ 0,
k = 1, ...,
r), (12)
а линейную функцию (13) запишем в виде
f +
cjxj =
c0. (13)
Здесь базис В = {х1, ..., xr}.
Оформим систему равенств (12) и (13) в виде таблицы 1 (матрицы).
Табл. 1 называется симплекс-таблицей. В табл. 1 мы приписали некоторую добавочную матрицу ||dij|| размера r × r и добавочную строку (d1, ..., dr). Введем в рассмотрение векторы
D = (с0, d1, ..., dr), Dk = (bk, dk1, ..., dkr), k = 1,2, ..., r.
Базис В называется положительным, если все векторы Dk(k = 1, ..., r) положительные (Dk > 0). Например, если матрица ||dij|| единичная  , то базис В положительный, потому что для любого k = 1, ..., r либо bk > 0, либо первый отличный от нуля элемент k-й строки матрицы ||dij|| равен 1 > 0.
, то базис В положительный, потому что для любого k = 1, ..., r либо bk > 0, либо первый отличный от нуля элемент k-й строки матрицы ||dij|| равен 1 > 0.
Будем считать, что числа dij подобраны так, что базис В положительный и матрица ||dij|| невырожденная (т. е. определитель, порожденный матрицей, отличен от нуля). Вектор D выбираем произвольно. Можно считать, что D = (c0, 0, ..., 0).
В дальнейшем при переходе от базиса В к другому базису В' записи систем ограничений (12) и линейной функции (13) будут изменяться, этому соответствует изменение табл. 1 с помощью некоторых элементарных преобразований (см. § 4.7), которые мы распространяем и на добавочную матрицу ||dij|| и добавочную строку (d1, ..., dr). В результате векторы Dk и D будут соответственно изменяться.
Напомним, что в случае III0 существует j0 (r + 1 ≤j0≤ п) такое, что сj0 > 0, и ak0j0 > 0, k ∈ е, где е - непустое множество и, кроме того, bk = 0 хотя бы для одного k ∈ е.
262
Индексов j0, для которых имеет место III0, может быть несколько. Не имеет значения, какой из них надо взять. Но, если мы остановились на некотором j0, то индекс k0 предлагается выбрать следующим образом:
Dk0 =
Dk. (26)
Элемент а*0/0 разрешающий. В табл. 1 мы его поместили в рамку.
Минимум в (26) достигается для одного k0, потому что если бы нашлось k1 ∈ е, для которого
Dk1 =
Dk0,
то в матрице ||dij|| были бы две пропорциональные строки и она была бы вырожденной.
Замечание 3. Так как мы рассматриваем случай III0, то среди k ∈ е имеются такие, для которых bk = 0, поэтому
Dk =
Dk,
т. е. индекс k0 находится среди таких k ∈ е, для которых bk = 0.
В п. 28.5 мы брали в качестве k0 одно из значений k ∈ е, для которых bk = 0. Но таких значений может быть несколько. В данном способе среди них выбирается одно такое определенное значение, обращающее в минимум
Dk.
Мы уже знаем, что в данном случае III0 базис В = {x1, ..., хr} можно заменить на другой базис B’ = {x1, ..., xk0-1, xj0, xk0+1, …, xr}, которому соответствует система ограничений, эквивалентная системе (12):
263
 (27)
(27)
b
≥ 0 (
k = 1, ...,
k0 - 1,
j0,
k0 + 1, ...,
r), и линейная функция
f + c
xr+1 + … +
xxj0-1 +
cxk0 +
cxj0+1 +
+ … +
cxn =
c (28)
Системе равенств (27)-(28) соответствует таблица 2.
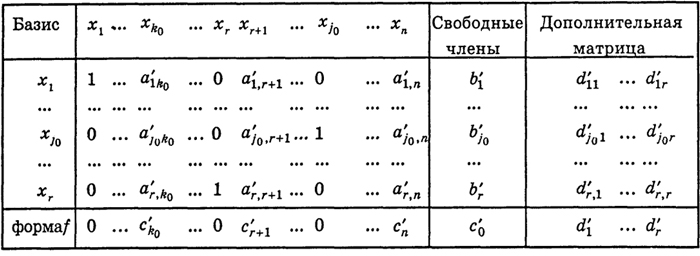
Табл. 2 получается из табл. 1 следующим образом. Делим k0-ю строку табл. 1 на разрешающий элемент ak0j0 (≠0).
Этим k0-е уравнение системы (12) остается равносильным прежнему. Добиваемся теперь, чтобы в j0-м столбце на остальных местах (k ≠ k0) были нули. Для этого из k-й строки вычитаем измененную k0-ю строку, умноженную на число akJ0. (Эту процедуру мы распространяем и на строки добавочной матрицы, в результате числа dkj переходят в числа d
).
Этот прием соответствует замене k-го уравнения разностью между ним и видоизмененным k0-м уравнением, умноженным на число аkj0 , что приводит к системе (27), равносильной системе (12).
Посмотрим, как видоизменяются векторы Dk, Так как базис B положительный и рассматривается случай III0, то bk0 = 0и
264
Таблица 2
265
Dk0 = (0, dk01, …, dk0r) > 0,
поэтому
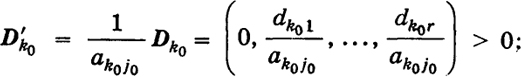
для k ≠ k0, k ∈ е (akj0 > 0)
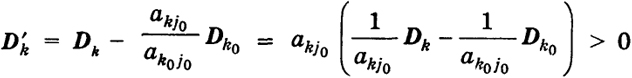
в силу правила выбора k0 ∈ е и его единственности (см. (26)); для k ≠ k0, k ∈ е (akj0 ≤ 0), очевидно,
D = Dk -
Dk0 > 0.
Чтобы получить последнюю строку табл. 2, надо из последней строки табл. 1 вычесть видоизмененную k0-ю строку, умноженную на cj0 . Вектор D = (с0, d1, ..., dr) переходит в вектор
D’ = D -
Dk0.
Так как cj0 > 0, аk0j0 > 0, то
D' - D = -
Dk0 < 0,
т. е. D' < D.
Новые коэффициенты линейной функции f имеют вид
c = -
cj0,
c =
cj -
cj0(
j =
r + 1, ...,
j0 - 1,
j0 + 1, ...,
n).
Таким образом, мы пришли к положительному базису В’.
Чтобы табл. 2 была полностью аналогичной табл. 1, рекомендуем в табл. 2 переставить местами столбцы, отвечающие переменным xj0 и xk0 .
266
Если для базиса B’ снова будет иметь место случай III0, то к нему можно опять применить описанный прием, который приводит к новому базису B", отличному не только от B', но и от В, потому что
D" < D' < D.
Замечание4. Если в процессе применения симплекс-метода мы пришли к циклу (см. (25)), то можно взять один из базисов цикла, например В = Bs0+l, и последовательно применять к нему описанный выше способ однозначного получения нового базиса на основании правила (26) выбора разрешающего элемента. Этим гарантируется получение каждый раз базиса, отличного от всех предшествующих. Так как количество возможных базисов конечно, то мы для некоторого базиса цепи обязательно придем к случаям I, II или III+. В последнем случае возникает базис В', для которого fB > fB’. Базисы, возникшие после В', отличаются от базиса В и всех ему предшествующих базисов. Они могут создавать циклы, но состоящие из новых базисов, отличных от B и ему предшествующих.
Итак, вычисления по симплекс-методу производятся следующим образом:
- исследуются уравнения (12) с базисом Б и функция f; если будут иметь место случаи I или II, то задача на минимум f решена;
- если будет случай III+, то переходим к новому базису на основании (16), составляя таблицы 1 и 2 без добавочной матрицы ||dij||;
- если же будет случай III0, то можно продолжать наш процесс в надежде, что не случится цикла. Практика показывает, что циклы бывают очень редко;
- все же, если случится цикл, то придется, отправляясь, как правило, от базиса Вs0 , двигаться дальше, применив добавочную матрицу ||dij||; рассуждения станут более сложными, но они имеют то преимущество, что на каждом их этапе s будут получаться все новые и новые базисы, отличные от всех предыдущих базисов;
- для базиса Bs0 мы выбираем матрицу ||dij|| и вектор D = (c0, d1, ..., dr) произвольно, как было указано выше;
- дальнейшие базисы, следуя методу, получаются определенным образом, а вместе с ними определенным образом преобразуются матрицы ||dij|| и вектор D;
267
- через конечное число шагов мы выясним, что inf f = = -∞, или же найдем конечный минимум f.
Проследим симплекс-метод на конкретном примере.
Пример 5. Найти минимум линейной функции
f = 0 - (
x1 - 150
x2 +
x3 - 6
x4)
при ограничениях
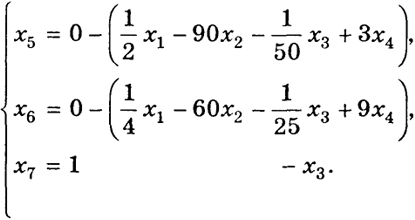
Решение. Здесь базис В = {х5, х6, х7}, и ограничения, и функция f записаны в форме (12)-(13). В данном случае c1 =
> 0 и в первом столбце матрицы ограничений имеются положительные элементы
а51 =
,
а61 =
. Отношения
b5BREAK/
а51 = 0,
b6BREAK/
а61 = 0. Поэтому
bkBREAK/
a61 = δ = 0
и этот минимум достигается на двух элементах k = 5, k = 6.
Таким образом, мы имеем случай III0 (j0 = 1). Чтобы избежать образования цикла, используем описанный выше способ однозначного выбора разрешающего элемента (см. (26)). Для этой цели составим таблицу 1*.
Здесь D1 = (0, 1, 0, 0), D2 = (0, 0, 1, 0) и 2D1 > 4D2.
Поэтому разрешающим элементом будет а61 =
, стоящий на пересечении строки для
х6 и столбца для
х1. Эту строку и столбец мы выделяем стрелками, а разрешающий элемент обводим рамкой. Преобразуем эту таблицу в таблицу 2*.
268
Таблица Г

Разделим строку для х6 на а61 =
, т. е. умножим строку для
х6 на 4 и перенесем ее в табл. 2*.
Затем умножим вторую строку (видоизмененную) на а51 = - и вычтем из первой строки. Далее умножим вторую строку на c1 =
и вычтем из последней строки. Строку для
х7 переносим в табл. 2* без изменений (
ап = 0).
Кроме того, мы переставим местами столбцы для х6 и х1, тогда табл. 2* будет иметь вид:
Таблица 2*

269
Таким образом, базис В1 = {x5, x1, х7}. В табл. 2* коэффициент с2 = 30 > 0 (штрих мы опускаем) и в столбце для x2 имеется один элемент а52 = 30 > 0, который и будет разрешающим элементом (в табл. 2* мы поместили его в рамку). Проводя преобразование табл. 2*, как и выше, мы перейдем к базису В2 = {x2, x1, x7}, т. е. из базиса В1 мы выводим переменную х5 и вводим переменную х2.
Таблица 3* будет иметь следующий вид (после перестановки столбцов для х2 и x5):
Таблица 3'

В последней строке табл. 3* имеется только один положительный коэффициент c3 =
> 0. В столбце для
х3 все элементы также положительны. В данной таблице
D1 = (0,
, -
, 0),
D2 = (0, 8, -12, 0),
D3 = (1, 0, 0, 1). Сравнивая векторы 500
D1,
D2,
D3, находим, что минимальным будет вектор 500
D1 и, следовательно, разрешающим элементом будет
а23 =
> 0. Минимум (16) равен нулю, т. е. мы опять имеем случай III
0. Преобразуя табл. 3*, получим таблицу 4*.
270
Таблица 4*
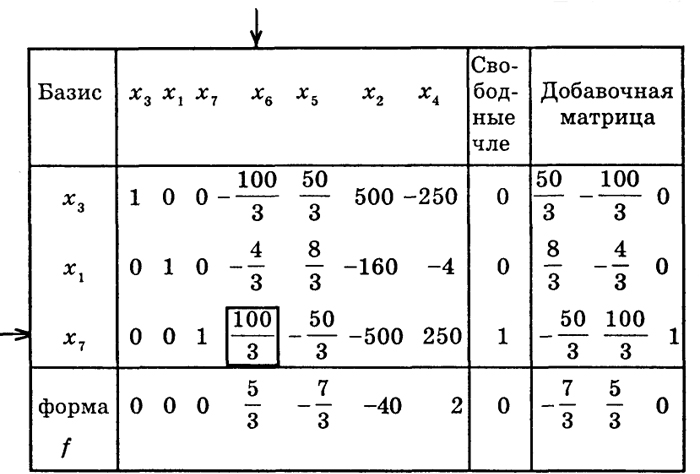
Таблица 5*
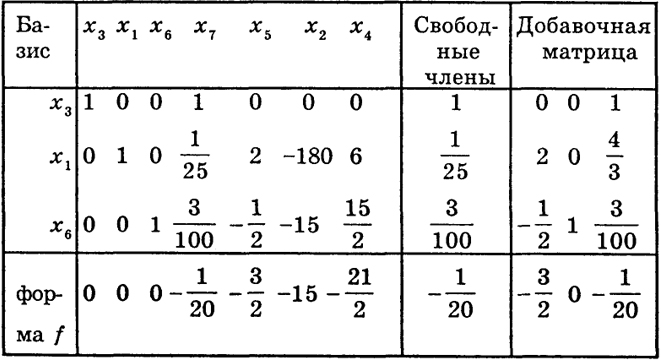
271
Здесь базис В3 = (x3, х1, x7}, с6 =
> 0 и в столбце для
х6 имеется только один положительный элемент
а76 =
> 0, который и будет разрешающим элементом. Минимум (16) равен
> 0, т. е. мы имеем случай III
+. Преобразуя табл. 4*, получим таблицу 5*.
В последней строке табл. 5* все коэффициенты cj (j = 7, 5, 2, 4) отрицательные, следовательно, minf =
(случай I).
Базис В4 = (x3, x1, х6}. Из табл. 5* видно, что базисное решение имеет вид х3 = 1, x1 =
,
х6 =
,
х7 =
x5 =
x2 =
x4 = 0.
Замечание 5. Если бы мы не следовали правилу однозначного выбора разрешающего элемента, то могли бы получить цикл, выбирая базисы в следующей последовательности:
В = {x5, x6, x7} → B1 = {x1, x6, x7} → B2 =
= {x1, x2, x7} → B3 = {x3, x2, x7} → B4 =
= {x3, x4, x7} → B5 = {x5, x4, x7} → B6 =
= {x5, x6, x7} = B.
Замечание 6. Отметим, что на каждом этапе, начиная с первого, можно было бы изменять нумерацию переменных, приводя систему ограничений и функцию f к виду (12), (13).
28.8. Условия существования базиса. Поясним, как можно привести систему ограничений (4)
akjxj =
bk (k = 1, ..., m) (4)
к системе вида (12)
272
xk = βk =
α
kjxj (β
k ≥ 0,
k = 1, ...,
r), (12)
т. е. выясним, когда переменные x1, ..., хr образуют базис.
Как нам известно, система (4) разрешима (совместна) тогда и только тогда, когда ранг матрицы

равен рангу расширенной матрицы
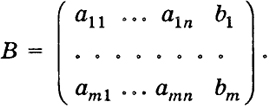
Пусть r = ранг А = ранг В. Тогда можно указать r таких уравнений системы (4), что всякое решение системы, состоящей из этих r уравнений, есть решение системы (4). Будем считать, что для данной системы (4) r = т и, кроме того, т < п, потому что при т = п существует только одна точка n-мерного пространства, являющаяся решением системы (4).
Кроме того, всегда можно добиться путем перенумерации переменных того, чтобы

Теорема 2. Для того чтобы неизвестные x1 ..., хт из системы (4) образовывали базис, необходимо и достаточно, чтобы
Δk/Δ ≥ 0 ∀k = 1, т,
где Δk - определитель, получающийся из определителя Δ заменой k-го столбца столбцом свободных членов системы (4).
273
Доказательство. Пусть
≥ 0,
k = 1, ...,
т. Применяя правило Крамера (см. § 4.2), имеем
(k - 1, ...,
m)
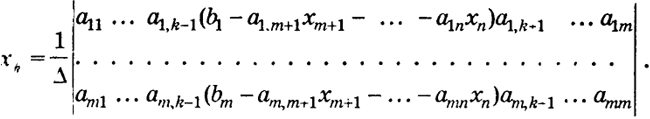
Учитывая свойства определителей, получаем равенства вида (12)
xk =
-
α
kjxj (
k = 1, …,
m),
где число αkj равно определителю, который получается из определителя Δ заменой k-то столбца соответственно на j-й столбец матрицы A (j = m + 1, ..., п), деленному на Δ. Например,
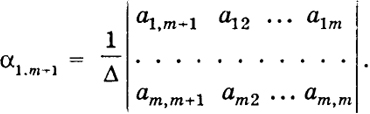
Обратно, пусть система х1, ..., хт есть базис, т. е. выполняются соотношения (12). Для матрицы равенств (12)
Δ* = 1, Δ
= β
k,
= β
k ≥ 0.
Допустимыми элементарными преобразованиями эта матрица переходит в матрицу равенств (4). При этом определители Δ* и Δ
переходят в определители Δ и Δ
k пропорционально. Поэтому
= β
k ≥ 0.
Пример 6. Найти базисные переменные в системе ограничений
274
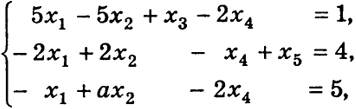
где α - некоторое число.
Решение. Если α ≤ 0, то система ограничений несовместна в области xj ≥ 0 (j = 1, ..., 5). Поэтому будем считать а > 0. Выясним, при каком а элементы x1, х2, х3 будут базисом. Имеем
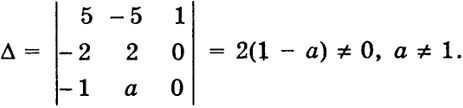
Далее,
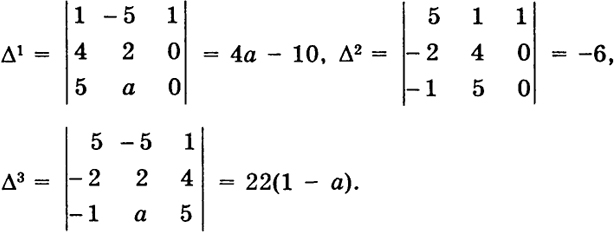
Отсюда
=
≥0, 1 <
a ≤
;
=
> 0,
a > 1;
= 11 > 0.
Таким образом, при 1<а<
все отношения Δ4
k/Δ ≥ 0 (
k = 1, 2, 3) и {
x1,
х2,
х3} - базис.
Для того чтобы написать систему (12), нет необходимости вычислять все нужные определители. Надо просто преобразовывать матрицу 5, как мы это делали в § 4.7.
Пусть а = 2. Получим базис из элементов х1, х2, х3, Для этой цели будем матрицу В преобразовывать так,
275
чтобы в первых трех столбцах по главной диагонали стояли 1, а на остальных местах - 0. Итак,

Последняя матрица определяет следующую систему уравнений:
x1 - x4 + x5 = 1
x2 -
x4 -
x5 = 3
x3 -
x4 +
x5 = 11.
276
Аналогичным образом можно проверить, при каком а переменные х1. х2, х5 образуют базис.
28.9. Задачи. Найти минимум функции f(x) = х4 - х5 при ограничениях:
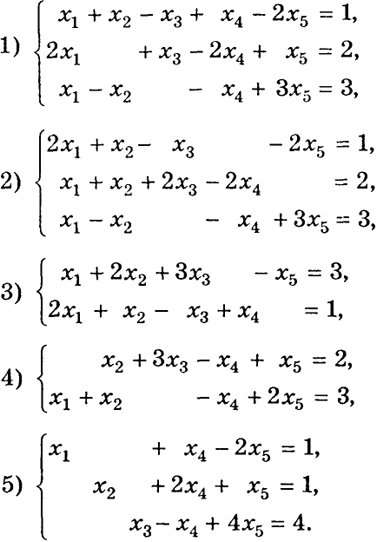
Приведем решение первой задачи. Итак, необходимо найти минимум линейной формы f(x) = х4 - х5 при ограничениях
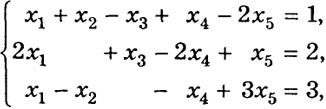
Согласно рассмотренной выше теории мы должны определить свободные переменные и выделить какой-либо базис, чтобы затем применить симплекс-метод для нахождения минимума функции f.
Так как в системе ограничений три уравнения, то в каждый базис входят какие-либо три переменные из x1,, х2, х3, х4, х5 Всего из пяти элементов можно составить десять различных комбинаций по три элемента
277

В принципе, мы должны проверить все тройки элементов и убедиться, какие из них являются базисами.
Выясним, будут ли элементы x1, x2, х3 образовывать базис. Определитель Δ, составленный из коэффициентов при этих неизвестных в системе ограничений, имеет вид
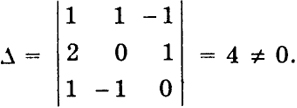
Далее,
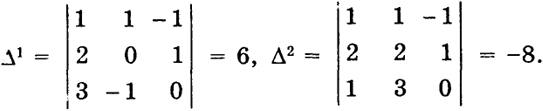
Отношение
= -2 < 0, следовательно, согласно теореме 2 п. 28.8 элементы
x1,
x2,
х3 не образуют базиса. Проверим тройку
x1,
х3,
х4:
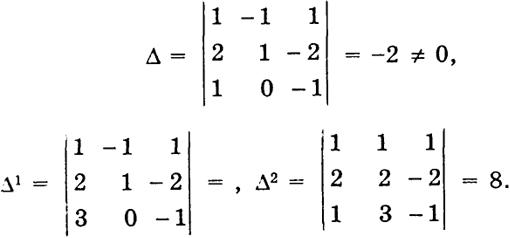
Отношение
= -4 < 0 и тройка
x1,
x3,
х4 также не образует базиса.
Исследуем тройку x1, x4, x5:
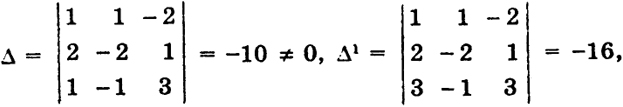
278
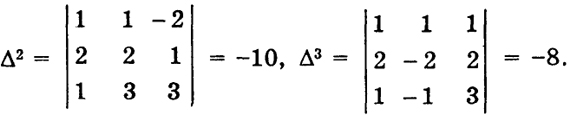
Таким образом, в данном случае все отношения
(
k = 1, 2, 3) положительны и по теореме 2 п. 28.8 элементы
x1,
x4,
х5 образуют базис.
Чтобы написать систему ограничений вида (12), преобразуем матрицу В системы ограничений к необходимому виду. Предварительно переставим столбцы коэффициентов при х4 и х5 соответственно на второе и третье места.
Тогда
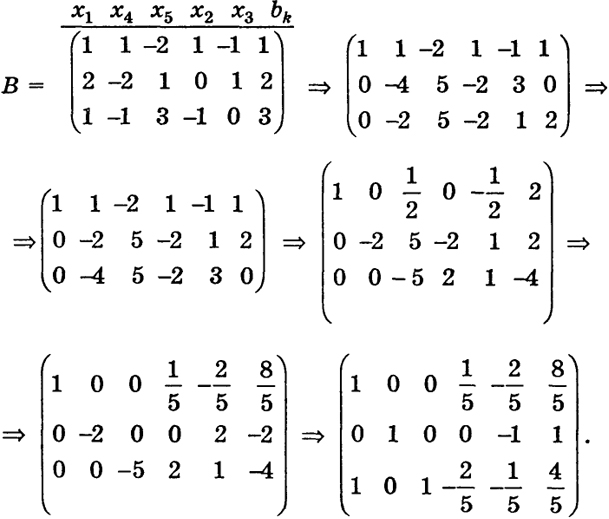
Последняя матрица определяет систему уравнений
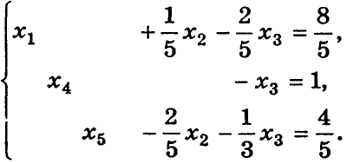 (27)
(27)
279
Линейная форма f через свободные переменные х2 и x3 запишется следующим образом:
f(x) = x4 - x5 =
-
x2 +
x3
или f +
x2 -
x3 =
Таким образом, теперь необходимо найти минимум линейной функции
f +
x2 -
x3 =
при ограничениях (27).
Здесь базис B1 = {x1, x4, x5}, ограничения и функция f записаны в форме (12), (13), и мы можем начать применение симплекс-метода.
В данном случае с2 =
> 0 и в первом столбце матрицы ограничений имеется положительный элемент
a12 =
> 0.
Отношение
= 8 > 0, т. е. мы имеем случай III
+ и
а12 - разрешающий элемент.
Составим первую симплекс-таблицу:
Таблица 6*
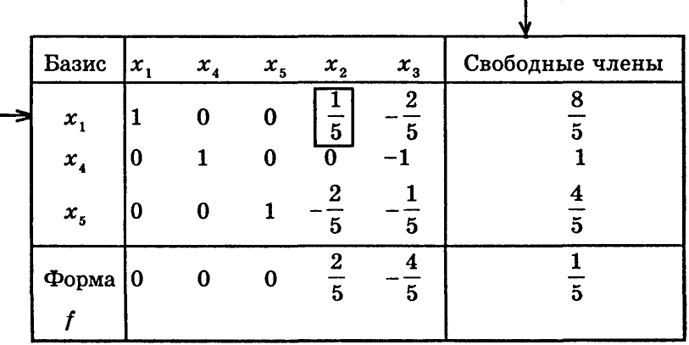
280
Здесь разрешающий элемент а12. Преобразуем таблицу 6* в таблицу 7*. Строку для xl умножим на 5 и перенесем ее в табл. 7*. Строку для х4 перенесем в табл. 7* без изменений (так как а42 = 0).
Затем умножим первую строку на 2 и прибавим результат к последней строке. Далее умножим первую строку на 2 и вычтем из строки для формы f. Кроме того, переставим местами столбцы для xl и х2. В результате табл. 7* будет иметь следующий вид:
Таблица 7*
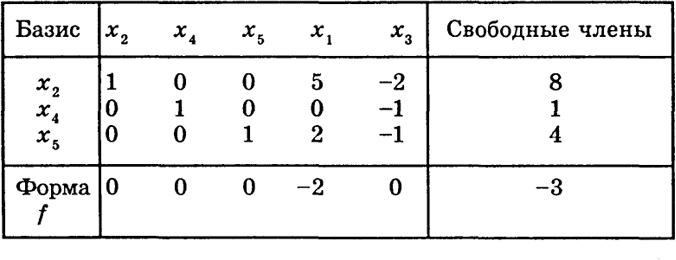
В табл. 7* коэффициенты формы f неположительны (с1 = -2, с3 = 0), поэтому при ограничениях (27)
f = -3,
и задача решена.
Замечание 7. Можно было бы исследовать все десять троек из элементов x1, х2, х3, х4, х5. Затем, найдя все базисы Bj(j = 1, 2, ..., j0; j0 < 10), мы можем найти минимум f при ограничениях (27) как минимальное значение среди fB1 , ..., fBj0 .
281
