27.1. Общие рассмотрения. В § 6 мы условились называть точкой или вектором n-мерного пространства Rn систему чисел (x1, ..., хп) и обозначать буквой х:
х = (х1, ..., хn).
Числа х. назывались координатами точки (вектора) или компонентами вектора х.
В § 7 мы определили отрезок [x0, у°], соединяющий точки
x0 = (x
, …,
x),
y = (
y, …,
y),
как множество точек х ∈ Rn, которые можно представить с помощью равенства
х = λx0 + μу0 (λ ≥ 0, μ ≥ 0, λ + μ = 1).
Точки x0, у0 называются концами отрезка [x0, y0]. Будем называть х0 начальной точкой отрезка [х0, у0], а y0 - его конечной точкой. Тогда можно считать, что [x0, у0] есть направленный отрезок с начальной точкой х0 и конечной точкой у0.
Как в случае трехмерного пространства, направленный отрезок [x0, у0] будем считать равным вектору
y0 - x0 = (y
-
x, …,
y -
x).
Если к векторам х0, у0 прибавить произвольный вектор
223
a = (a1, …, an)
то получим векторы
x' = x0 + a, y' = y0 + a,
для которых, очевидно,
у' - x' = у0 - х0.
Это показывает, что точки х' = х0 + а, у' = у0 + а, каков бы ни был вектор а, определяют один и тот же вектор, равный у0 - x0.
Направленный отрезок [0, х], начало которого есть нулевая точка 0, а конец - точка х, называют радиус-вектором точки х.
Итак,
х = (x1, …, xn)
есть точка Rn, x также есть радиус-вектор точки х, т. е. направленный отрезок [0, х] и, наконец, х может обозначать вектор, определяемый любым отрезком [x0, у0], для которого у0 - х0= х.
Пример 1. Направленные отрезки [х1, у1], [х2, у2], где
х1 = (0, 0, .... 0), у1 = (1, 1, ..., 1),
х2 = (3, 3, ..., 3), у2 - (4, 4, .... 4)
равны одному и тому же вектору a = (1, 1, ..., 1).
27.2. Плоскость в Rn. Зададим п действительных чисел А1..., Ап, одновременно не равных нулю, т. е. таких, что выполняется неравенство
A > 0
Зададим также действительное число В.
По определению геометрическое место точек х = (х1, ..., хп), удовлетворяющих уравнению
Ajxj +
B = 0(1)
224
называется плоскостью, а уравнение (1) называется уравнением этой плоскости.
Будем еще говорить: плоскость (1) вместо того, чтобы говорить: плоскость, определяемая уравнением (1).
При n = 3 плоскость (1) есть реальная плоскость.
Если умножить уравнение (1) на произвольное число М ≠ 0, то получим уравнение
Axj +
В' = 0 (
а =
MAj, (
j = 1, ...,
п),
В' =
МB), (1’)
эквивалентное уравнению (1).
Таким образом, уравнения (1) и (1') определяют одно и то же геометрическое место точек. Учтем еще, что
(
A)
2 =
M2 A > 0.
Но тогда уравнения (1) и (1') суть уравнения одной и той же плоскости.
Систему чисел A1, ..., Ап удобно мыслить как вектор
А =(А1, …, An).
Этот вектор заведомо ненулевой, потому что его длина положительна:

Как мы отмечали выше, буквы х = (х1, ..., хп) обозначают не только точки пространства Rn, но и радиус-векторы точек х. Но тогда левую часть уравнения (1) можно записать как скалярное произведение векторов А и х:
A1x1 + ... + Апxп ≡
Ajxj = (
А,
х),
а само уравнение (1) записать в виде
(А, х) + В = 0.
Эквивалентное же ему уравнение (1’) запишется в виде
(A', х) + В' = 0, (2')
где А' = МA, М ≠ 0, В = MB.
225
Таким образом, А' есть вектор, коллинеарный вектору А, т. е. А' получается из вектора А умножением его на число М ≠ 0. Число В' тоже получается из числа В умножением последнего на это же число М.
27.3. Уравнение плоскости в нормальном виде. Среди векторов А' особый интерес представляет единичный вектор, т. е. вектор, имеющий длину 1.
Чтобы получить его, множитель М надо подобрать так, чтобы оказалось, что |А'| = 1 (|А'|2 = M2
А ).
Отсюда ясно, что

Будем число М всегда выбирать так, чтобы при В ≠ 0 число р = -MB было положительным. Если В = 0, то за число М можно брать любое из двух возможных его значений.
При таком выборе числа М вектор А' = МА будет единичным, и мы его обозначим через v = (v1, ..., vn), т. е.
vj = MAj (j = 1, ..., п),
v =
М2]Г
A = 1.
В силу введенных обозначений уравнение (20 запишется:
vjxj =
p (3)
где
v = 1,
p ≥ 0 (4)
Уравнение (3), где числа vj и р удовлетворяют условиям (4), называется уравнением плоскости в Rn в нормальном виде.
Уравнение (1), где А1, ..., Аn, В - произвольные числа, но числа А1, ..., Ап одновременно не равны нулю, называется уравнением плоскости в Rn в общем виде.
226
Мы доказали, что любое уравнение плоскости в общем виде может быть приведено к нормальному виду умножением на определенное выше число М. Число М называется нормирующим множителем.
Очевидно и обратное, если умножить уравнение плоскости (3) в нормальном виде на произвольное не равное нулю число, то получим ему эквивалентное уравнение вида (1), где числа А. одновременно не равны нулю.
27.4. Уравнение плоскости в векторной форме.
Уравнение (3) можно еще записать, очевидно, в виде
(v, х) = р. (3’)
Введем в рассмотрение вектор
а = pv = (pv1 ..., pvn) = рМА.
При р > 0 он направлен в сторону единичного вектора v и имеет длину, равную р: |
а|= |
pv| =
p|
v| =
p.
Если р = 0, то а = 0.
Помножим равенство (3') на р > 0 и учтем, что
р2 = (pv, pv);
тогда получим
(pv, х) = (pv, pv),
или
(а, х) = (а, а).
Учитывая свойства скалярного произведения, последнее равенство можно записать в виде
(а, х - а) = 0. (5)
Обратными рассуждениями из (5) можно снова получить (3'). Это показывает, что равенство (5) эквивалентно уравнению плоскости (1), т. е. уравнение (5) можно считать уравнением рассматриваемой нами плоскости (1). Говорят еще, что уравнение (5) есть уравнение плоскости (1) в векторной форме при В ≠ 0 (т. е. р > 0).
Таким образом, плоскость (1) - это геометрическое место точек х, которые удовлетворяют уравнению (5).
227
Пусть теперь р = 0 или, что все равно, В = 0.
Тогда уравнение (3') имеет вид
(v, х) = 0. (5’)
Уравнение (5') и есть уравнение плоскости (1) в векторной форме при В = 0. Оно выражает, что множество всех точек плоскости (1) состоит из всех точек х ∈ Rn, удовлетворяющих (5’), где 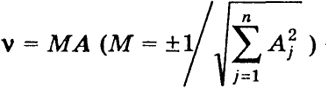 любой из двух возможных единичных векторов.
любой из двух возможных единичных векторов.
27.5. Геометрическая интерпретация уравнений. Условимся говорить, что вектор с ортогонален к отрезку [x0, у0], если он ортогонален к вектору у0 - x0, т. е. если
(с, у0 - x0) = 0.
Будем также говорить, что вектор с ортогонален к плоскости L, если он ортогонален к любому отрезку, принадлежащему L.
Покажем, что если точки х1 и х2 принадлежат плоскости (5), то и отрезок [х1, х2] принадлежит этой плоскости. В самом деле, по условию
(a, х1 - а) = 0, (а, х2 - а) = 0.
Далее, произвольная точка х отрезка [х1, х2] может быть записана в виде
х = λx1 + μx2 (λ ≥ 0, μ ≥ 0, λ + μ = 1),
поэтому
(а, х - а) = (а, λx1 + μх2 - а) =
= (a, λx1 + μx2 - (λ + μ)а) = (а, λ(х1 - а) + μ(x2 - а)) =
= (а, λ(x1 - а)) + (a, μ(x2 - а)) =
= λ(a, х1 - а) + μ(a, х2 - а) = λ ∙ 0 + μ ∙ 0 = 0.
Таким образом, х принадлежит плоскости (5), а следовательно, и весь отрезок [х1, х2] принадлежит этой плоскости.
228
Из уравнения (5) видно, что точка а принадлежит к этой плоскости: (а, а - a) = (а, 0) - 0.
В силу вышесказанного плоскость (1) можно определить как геометрическое место точек х ∈ Rn таких, что разность х - а, где х - радиус-вектор точки x, ортогональна к вектору а.
Покажем еще, что вектор
A = (A1, ..., Аn)
ортогонален к плоскости (5).
В самом деле, в силу равенства а = рМА (р > 0) вектор А коллинеарен вектору а и, следовательно, он ортогонален к любому вектору х - а, принадлежащему, плоскости (5), т. е. ортогонален к плоскости (5) или, что все равно к плоскости (1).
Итак, числа A1 ..., Ап в уравнении плоскости (1) имеют геометрический смысл - вектор А = (А1, ..., Ап), составленный из коэффициентов при х, этого уравнения, ортогонален к плоскости (1).
Если р = 0 или, что все равно, В = 0, то рассматриваем уравнение (5'), эквивалентное уравнению (1). Уравнение (5') выражает, что множество всех точек х плоскости (1) состоит из точек х, радиус-векторы которых ортогональны к вектору v = МА.
В этом случае вектор А = (А1, ..., Ап), коллинеарный вектору v, снова ортогонален к плоскости (1).
27.6. Уравнение плоскости, проходящей через n точек
Теорема. Пусть задано п точен
x1 = (x
, …,
x),
xn = (
x, …,
x)
определяющих матрицу
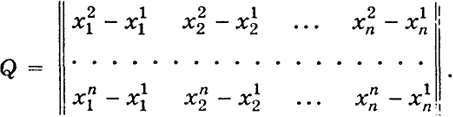 (6)
(6)
229
Тогда если ранг Q равен п - 1 (ранг Q = п - 1), то через указанные п точек можно провести плоскость и притом единственную.
Если же ранг матрицы Q меньше чем п - 1 (ранг Q < п - 1), то через указанные п точек можно провести бесконечное множество плоскостей.
Доказательство. Пусть ранг Q = п - 1.
Уравнение искомой плоскости запишем в виде
Ajxj +
B = 0. (7)
Так как эта плоскость должна проходить через точку х1, то должно удовлетворяться равенство
Ajx +
B. (8)
Вычитая равенство (8) из равенства (7), получим уравнение
Aj(
xj - x) = 0. (9)
справедливое для всех точек х искомой плоскости.
Так как точки х2, ..., хп должны принадлежать искомой плоскости, то их координаты должны удовлетворять уравнению (9), т. е. должны выполняться равенства
| Aj(x - x), |
| ………….. |
| Aj(x - x) = 0. |
(10)
Итак, числа Аj должны быть решениями однородной системы, состоящей из равенства (9) и равенств (10), где х = (x1, ..., хп) - произвольная точка искомой плоскости. Но числа Аj должны быть одновременно не равны нулю. Поэтому определитель однородной системы должен равняться нулю:
230
 (11)
(11)
для всех точек х = (x1, ..., хп) искомой плоскости.
Уравнение (11) и есть уравнение искомой плоскости. Если определитель левой части этого уравнения разложить по элементам первой строки, то получим уравнение вида (9) с коэффициентами Aj, равными определителям (п - 1)-го порядка, порождаемым матрицей Q с соответствующим знаком. По условию среди этих определителей есть хотя бы один, не равный нулю.
Первое утверждение теоремы доказано.
Пусть теперь ранг матрицы Q меньше п - 1 (ранг Q < п - 1). Тогда, рассуждая, как прежде, мы придем к тому, что любая точка х плоскости, проходящей через заданные п точек, должна удовлетворять системе, состоящей из уравнения (9) и уравнений (10) при некоторых постоянных a1, ..., Ап.
Так как ранг Q ≤ п - 2, то система (10) имеет бесконечное число решений A1 ..., Ап. При этом по крайней мере два из чисел Аj, пусть А1 и А2 могут быть любыми независимыми друг от друга числами - им можно придавать любые числовые значения.
Если подставить найденные числа А1, ..., Ап в уравнение (9), то различным не пропорциональным между собой парам А1, А2 будут соответствовать заведомо разные плоскости, проходящие через заданные п точек.
Второе утверждение теоремы доказано.
Уравнение (11) можно записать в форме
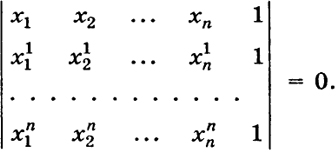
231
27.7. Условия ортогональности и параллельности плоскостей. Угол между двумя плоскостями в Rn
Ajxj +
B = 0, (12)
Axj +
B’ = 0 (13)
определяется по аналогии с трехмерным случаем. А именно, углом между плоскостями (12), (13) называется угол φ между векторами А - (А1, ..., Ап) и А' = (А1, ..., Аn), которые, как мы выяснили, перпендикулярны к плоскостям (12) и (13) соответственно.
На основании формулы (8) § 6 имеем

Плоскости (l2) и (13) перпендикулярны тогда и только тогда, когда cos φ = 0 , т. е.
AjA = 0 (14)
Две плоскости (12), (13) параллельны тогда и только тогда, когда перпендикулярные к ним векторы А и А' коллинеарны (А = λА')" т. е. когда
=
= … =
. (15)
27.8. Уравнение плоскости, проходящей через точку. Если точка (х, …, x) = Q0 лежит на плоскости
232
Ajxj +
B = 0, (16)
то ее координаты удовлетворяют уравнению этой плоскости
Ajx +
B = 0. (17)
Вычитая (17) из (16), получаем
Aj(
xj -
x) = 0. (18)
Уравнение (18) называется уравнением плоскости, проходящей через точку Q0 = (х, …, х).
В векторной форме уравнение можно записать так:
A(ρ - ρ0) = 0, (18')
где
А = (А1, ..., Аn), ρ = (x1, ..., хп),
ρ0 = (x, …, x).
Здесь, как мы знаем, вектор А перпендикулярен плоскости (16), ρ - радиус-вектор текущей ее точки, ρ0 - радиус-вектор заданной ее точки Q0.
27.9. Прямая в пространстве Rn. Уравнения прямой в пространстве Rn можно вывести по аналогии с трехмерным пространством Rn (см. § 10).
Прямой L в Rn, проходящей через точку Q0 = (х, ..., х) и направленной в сторону вектора а = (а1, ..., ап) (|а| > 0), называется геометрическое место точек Q = (x1, ..., хп) ∈ Rn удовлетворяющих уравнениям
 (19)
(19)
где t - действительная переменная, пробегающая
233
интервал (-∞, ∞). Удобно считать, что вектор а приложен к точке Q0.
Уравнения (19) называются параметрическими уравнениями прямой L.
Если ввести в рассмотрение радиус-векторы точек Q и Q0 прямой L:
ρ = (x1, …, xn), ρ0 = (x, …, x),
то уравнения (19) запишутся:
ρ - ρ0 = ta, (19')
т. е. вектор ρ - ρ0 коллинеарен вектору а.
Если действительная переменная (скаляр) t пробегает интервал (-∞, ∞), то конец радиус-вектора
ρ = ρ0 + ta
пробегает всю прямую L.
Уравнение (19') называется уравнением прямой в векторной форме.
Исходя из (19'), мы видим, что вектор а лежит на прямой L, потому что его начало Q0 имеет радиус-вектор ρ0, а конец - ρ0 + а. Оба эти вектора удовлетворяют уравнению (19') соответственно при t = 0 и t = 1 (см. § 7).
Если исключить параметр t из уравнений (19), то мы получим систему из (п - 1) уравнений:
=
= … =
. (19’’)
Уравнения (19’’) называются уравнениями прямой L в канонической форме или каноническом виде. Пусть заданы прямые
= … =
. (
L1)
= … =
. (
L2).
Углом между прямыми L1 и L2 называется угол φ между векторами
а = (a1, ..., an), b = (b1, ..., bn),
234
которые, как мы показали, лежат на соответствующих прямых L1 и L2. Они приложены соответственно к точкам (x, …, x), (y, …, y).
Пример 1. Написать уравнение плоскости, проходящей через точку Q0 = (х, ..., x) и перпендикулярно прямой, определяемой уравнениями
=
= … =
. (20)
Решение. Уравнение плоскости, проходящей через точку Q0, имеет вид (см. (18))
Aj(
xj -
x) = 0. (21)
Искомая плоскость должна быть ортогональной прямой (20), т. е. ортогональной вектору Ъ = (b1, ..., bп).
С другой стороны, вектор А = (А1, ... , Ап) ортогонален плоскости (21). Поэтому векторы А и b коллинеарны: А = λb. Следовательно, уравнение искомой плоскости запишется:
bj(
xj -
x) = 0.
27.10. Расположение (п - 1) плоскостей. Пусть заданы уравнения (п - 1) плоскостей
Ах1 + ... + Axn + В1 = 0, (22,)
Ax1 + … + Аxn + Вn-1 = 0. (22n-1)
Если коэффициенты первого уравнения пропорциональны коэффициентам второго (А : А : ... : А = А : A : ... : а), то плоскости параллельны (см. 27.7).
Если указанная пропорциональность имеет место и для коэффициентов других уравнений, то все плоскости будут
235
параллельны между собой. В этом случае все определители (п - 1)-го порядка, порожденные матрицей ||A|| коэффициентов A уравнений (221) - (22n-1), равны нулю.
Если хотя бы один из определителей (п - 1)-го порядка матрицы ||A|| не равен нулю, то плоскости (221)-(22n-1) пересекаются по прямой. В самом деле, пусть для определенности
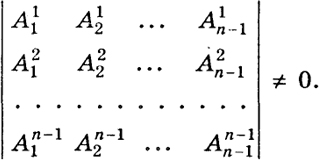 (23)
(23)
Тогда уравнения (221)-(22n-1) можно решить относительно x1, ..., хп-1 и мы получаем
 (24)
(24)
где α1, ..., αn-1 μ1, ..., μn-1 - некоторые числа.
Уравнения (24) эквивалентны следующим уравнениям:
= … =
=
. (25)
Мы видим, что при условии (23) уравнения (п - 1) плоскостей (221)-(22n-1) определяют прямую (25). Она проходит через точку (μ1, ..., μn-1, 0) и имеет направление вектора (α1, ..., αn-1, 1).
Пример 2. Найти угол между прямыми
=
=
=
,
=
=
=
,
236
Решение. Векторы а = (1, 2, 3,4), b = (4, 3, 2, 1) лежат на наших прямых, расположенных в четырехмерном пространстве R4. Поэтому угол φ между этими векторами и будет углом между прямыми:

φ = arccos
27.11. Расстояние от точки до плоскости. Пусть задана плоскость ∏, определяемая общим уравнением
Ajxj +
B = 0 (|
A|
2 =
A > 0), (26)
или векторным уравнением
(A, ρ) + В = 0, (27)
или же нормальным уравнением
(ρ, ν) - ρ (ρ ≥ 0), (28)
где A = (А1, ..., Аn), ρ - радиус-вектор текущей точки Q = (х1, ..., xn) плоскости ∏, ν = ±
, ρ = ±
.
Зададим некоторую точку Q0 = (x, ..., x). Радиус-вектор точки Q0 обозначим через ρ0.
Расстоянием от точки Q0 до плоскости ∏ называется длиной d отрезка, опущенного из нее на ∏.
Покажем, что
d = |(ρ - ρ0, ν)|, (29)
т. е. расстояние d до ν равно абсолютной величине проекции вектора ρ - ρ0 на направление единичного вектора ν = ±
(ортогонального к ∏).
На рисунках 53 а и 53 б изображена плоскость ∏ и точка Q0. На рис. 53 а точки О и Q0 находятся по разные
237
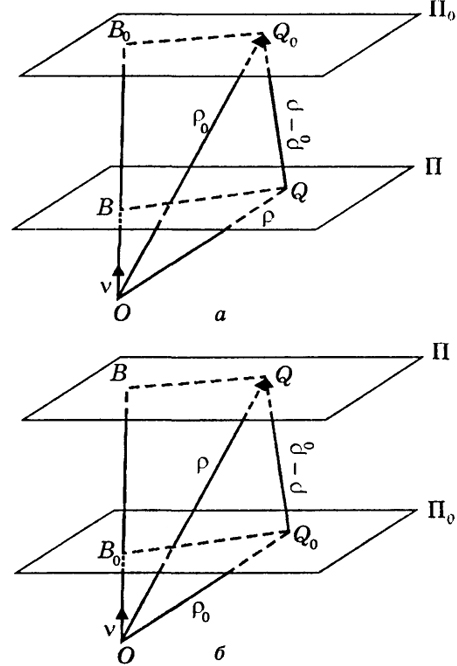
Рис. 53
стороны от ∏ (∏ пересекает OQ0). А на рис. 53 б - по одну сторону от ∏ (∏ не пересекает OQ0).
Через точку Q0 проведена плоскость ∏0, параллельная ∏. Из точки О проведена прямая, перпендикулярная к ∏ (и ∏0), пересекающая ∏ и ∏0 соответственно в точках В и В0. На ней отмечен единичный вектор ν, идущий от точки О по направлению к ∏.
Обратимся к рис. 53 а. Векторы ρ0 - ρ образуют острый угол. Проекция ρ0 - ρ на направление ν есть положительное число, равное длине отрезка |BВ0|, которая в свою очередь равна расстоянию от Q0 до ∏:
|ВВ0| = d = (ν, ρо - ρ).
238
На рис. 53 б ν образует острый угол с ρ0 - ρ и на этот раз расстояние от QO до ∏ равно
|BB0| = d = (ν, ρ - ρ0).
Оба полученные равенства объединяются равенством (29) или, что все равно, равенством:
d = l(ν, ρ0) - ρ|.
Таким образом, для того чтобы вычислить расстояние d от точки Q0 до плоскости ∏, надо записать уравнение плоскости ∏ в нормальном виде (28), перенести р в левую часть и подставить в последнюю (х, …, х) вместо (x1, ..., хп). Абсолютная величина полученного выражения и есть искомое число d.
На языке параметров плоскости, очевидно,

Пример 3. Найти расстояние d от точки

пространства Rn до плоскости
x1 + √2 x2 + √3 x3 + ... + √n xn + 1 = 0.
Решение. Согласно сказанному выше

27.12. Различные задачи.
Привести к нормальному виду уравнения следующих плоскостей (1-3):
1. 1х1 + 2х2 + ... + nxn = -1.
239
Ответ:
=
√ .
2. x + y + z + t = 0.
3.
= 1
Ответ:
√ xj =
√ .
4. Найти угол φ между плоскостями в R4:
(8 + √59)x1 + 2х2 + 3x3 + 4z4 = 0,
4х1 + 3х2 + 2x3 + (8 + √59)x4 = 1.
Ответ: φ =
.
5. Найти угол φ между плоскостями в R2n:
(-1)
jxj = 0,
xj = 1.
Ответ: φ =
(плоскости ортогональны).
6. Написать уравнение плоскости, проходящей через точки пространства Rn:
Q1 = (1, 0, …, 0),
Q2 = (0, 1, 0, …, 0 ),
.................
Qn = (0, …, 0, 1).
Ответ: х1 + х2 + ... + хп = 1.
7. Написать уравнение прямой, проходящей через точку (1, 2, ..., n) перпендикулярно плоскости:
nx1 + (n -1)x2 + … + 2xn-1 + xn = 4.
Ответ:
=
= … =
.
240
8. Написать уравнение плоскости в R4, проходящей через точки
Q1 = (1, 0, 0, 0), Q2 = (1, 1, 0, 0),
Q3 = (1, 1, 1, 0), Q4 = (1, 1, 1, 1).
Ответ: x1 = 1 (1 ◦ x1 + 0 ◦ х2 + 0 ◦ х3 + 0 ◦ х4 = 1).
241
