Уравнение
aklxkxl + 2
A1x1 +
B = 0, (1)
где akl = alk, A1, В - заданные постоянные числа, а х = (х1, х2, х3) - переменная точка в R3, определяет, вообще
196
говоря некоторое множество точек в R3, называемое поверхностью второго порядка. Если уравнение (1) не удовлетворяется ни одной действительной точкой х = (х1, x2, х3), то говорят, что оно определяет мнимую поверхность. Нас эти случаи не будут интересовать. В некоторых случаях уравнение (1) может определять пару различных или совпадающих плоскостей или одну-единственную точку. Но и такие множества мы будем называть поверхностями. Перечислим важнейшие частные случаи уравнения (1):
1) Эллипсоид
+
+
= 1 (
a, b ,c > 0).
2) Однополостный гиперболоид
+
-
= 1 (
a, b ,c > 0).
3) Двуполостный гиперболоид
-
-
= 1 (
a, b ,c > 0).
4) Эллиптический параболоид
+
= 2
z (
p, q > 0).
5) Гиперболический параболоид
-
= 2
z (
p, q > 0).
6) Конус второго порядка
+
-
= 0 (
a, b, c > 0 ).
7) Точка
х2 + у2 + z2 = 0.
197
8) Цилиндры второго порядка: цилиндр эллиптический
+
= 1 (a, b, > 0)
цилиндр гиперболический
-
= 1 (
a, b > 0),
цилиндр параболический
у2 = 2рх (р > 0),
пара пересекающихся плоскостей
а2х2 - b2у2 = 0 (а, b > 0),
пара параллельных или совпадающих плоскостей
х2 - а2 = 0 (а > 0),
z2 = 0,
прямая
х2 + у2 = 0.
При рассмотрении частных случаев уравнения (1) мы считали, что х = x1, у = х2, z = х3.
Можно доказать, что для каждого частного уравнения (1), если оно не определяет мнимую поверхность, можно найти прямоугольную систему координат, в которой это уравнение имеет один из перечисленных выше восьми видов. Это следует из общей теории § 22. Само преобразование уравнения (1) производится так же, как в § 24. Нахождение собственных значений λ1, λ2, λ3 сводится к решению кубического уравнения.
Укажем еще один путь нахождения собственных чисел и собственных векторов, который мы по сути дела уже рассмотрели в § 23 в двумерном случае. Собственные значения λ1, λ2, λ3 самосопряженного оператора А и
198
принадлежащие им нормированные векторы x1, х2, х3 (|хj| = 1, Ахj - λjхj, j = 1, 2, 3) можно находить следующим образом (обоснование см. ниже). Вводим определитель (аkl = alk):
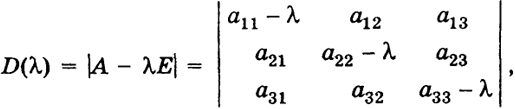
где Е - единичная матрица. Находим корни λ1, λ2, λ3 уравнения
|А - λE| = 0, (2)
которое называется характеристическим уравнением оператора AD(λj) = 0, j = 1, 2, 3). Это и есть собственные числа оператора А. Они действительные, причем они могут быть разными, но могут и совпадать - быть кратными. Таким образом,
D(λ) = (λ1 - λ)(λ2 - λ)(λ3 - λ).
Затем для корня λ1 ищем нетривиальное решение х = (х1, x2, x3) однородной системы уравнений:
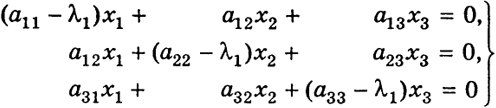 (3)
(3)
или соответствующего уравнения для оператора А - λ1Е:
(А - λ1Е)х = 0, (3')
где Е - единичная матрица и векторы х = (х1, х2, х3), 0 = (6, 0, 0).
Если λ1 - простой корень (т. е. в данном случае λ1 отлично от λ2 и от λ3), то ранг матрицы системы (3) необходимо будет равен двум (ранг (А - λ1Е) = 2), и мы получим единственный, с точностью до знака, вектор х1 = (х
,
х,
x), удовлетворяющий системе (3), т. е.
199
(А - λ1E)x1 = 0
или
Ах1 = λ1x1.
Если λ1 - корень второй кратности (λ1 = λ2 ≠ λ3), то система (3) необходимо имеет ранг, равный единице (ранг (А - λ1E) = 1), и будет иметь два ортонормированных решения х1 и х2 (|xl| = |х2| =1, (x1, х2) = 0), которые являются собственными векторами, принадлежащими собственному значению λ1:
Axj = λjxj (j = 1, 2, λ1 = λ2)
Наконец, если λ1 - корень третьей кратности (λ1 = λ2 = = λ3), то система (3) необходимо имеет ранг, равный нулю (ранг (А - λ3) = 0), и будет иметь три ортонормированных решения х1, х2, х3:
Axj = λjxj (j = 1, 2, 3, λ1 =λ2 = λ3).
Любые три ортонормированных вектора в R3 могут быть взяты в качестве собственных векторов x1, x2, х3, принадлежащих собственным числам λ1 = λ2 = λ3.
Обоснуем сказанное. Мы знаем, что в R3 существует система ортонормированных векторов x1, x2, x3 и действительные числа λ1, λ2, λ3 такие, что
Axj = λjxj (j = 1, 2, 3).
При этом можно указать ортогональную матрицу Λ такую, что (см. § 22)

Отсюда для переменного числа λ имеет место тождество
200
 (4)
(4)
(Λ(А - λE)Λ-1 = ΛАΛ-1 - ΛλEΛ-1 = ΛAΛ-1 - λΛΛ-1 = ΛАΛ-1 - λE).
Определитель матрицы А - λЕ мы обозначили выше через D(λ). Он, как это видно из (4), равен определителю матрицы, стоящей в правой части (4), так как
(λ1 - λ)(λ2 - λ)(λ3 - λ) = |Λ(А - λE)Λ-1| =
= |Λ||A - λE||Λ-1| = |А - λЕ| = D(λ).
Таким образом,
D(λ) = (λ1 - λ)(λ2 - λ)(λ3 - λ).
Мы получили, что корни многочлена D(λ) совпадают с собственными значениями λ1, λ2, λ3 оператора А. Они, таким образом, действительны.
Пусть λ1 - простой корень и, следовательно, λ1 ≠ λ2 и λ1 ≠ λ2. Тогда матрица справа в (4) при λ = λ1 имеет ранг, равный двум (ранг Λ(А - λ1Е)Λ-1 = 2), но тогда ранг (А - λ1E) = 2. Ведь решения однородной системы (3) и системы
 (5)
(5)
соответствующей матрице (4), преобразуются друг в друга при помощи ортогональной матрицы (системы (3) и (5) эквивалентны). Система же (5) имеет только одно (с точностью до знака) нормированное решение (±1, 0, 0). Но это возможно, лишь если ранг (А - λ1Е) = 2.
Можно дать и такое объяснение этого факта. Если предположить, что все определители второго порядка, порожденные матрицей А - λ1E, равны нулю, то тогда и
201
все определители второго порядка, порожденные матрицей Λ(А - λ1E)Λ-1, также будут равны нулю, так как эти определители являются линейными комбинациями определителей второго порядка из матрицы А - λ1Е. Но этого не может быть, ибо определитель, порожденный матрицей Λ(А -λ1E)Λ-1,

Если теперь λ1 = λ2 ≠ λ3, то, рассуждая аналогично, получим, что ранг (А - λ1Е) = 1, и тогда существует в точности два ортонормированных решения х1, х2 системы (3), соответствующих λ1 = λ2.
Наконец, при λ1 = λ2 = λ3 будет ранг (А - λ1Е) = 0, т. е. все элементы матрицы А - λ1Е равны нулю. В этом случае любой вектор х = (x1, х2, х3) является решением системы (3). Это приводит к тому, что любые три вектора х1, х2, х3, образующие ортонормированную систему, будут собственными векторами, принадлежащими собственному значению λ1 = λ2 = λ3.
Заметим, что в этой ситуации квадратичная форма уже приведена к сумме квадратов (а12 = а13 = а23 = 0, а11 = a22 = а33 = λ1).
Пример 1. Привести к каноническому виду квадратичную форму
x
+
x + 2
x1x2 + 2
x1x3 + 2
x2x3.
Здесь а11 = а22 = а12 = a13 = a23 = 1, a33 = 0. Составим характеристическое уравнение:
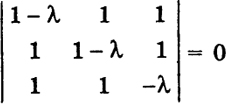
202
или
-λ(l - λ)2 + 2 - 2(1 - λ) + λ = 0, -λ(l - λ)2 + 3λ = 0.
Легко видеть, что λ = 0 является корнем этого уравнения. Найдем два других корня:
3 - (1 - λ)2 = 0, (1 - λ)2 = 3, 1 - λ = ±√3, λ = 1 ±√3.
Таким образом,
λ1 = 1 + √3, λ2 = 0, λ3 = 1 - √3,
т. е. мы получили случай: λ1 > λ2 > λ3.
Найдем собственный вектор х1. Для этого составим систему (3):
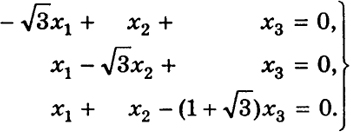
Любые два уравнения этой системы линейно независимы. Решая систему из двух первых уравнений, получаем
x1 =
x3,
x2 =
x3.
Таким образом, вектор

является решением системы и, нормируя его, получим собственный вектор

Найдем х2(λ2 = 0):
203
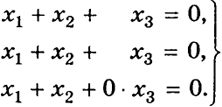
Решая систему из двух последних уравнений (так как определитель из коэффициентов при х2 и х3 не равен нулю), получим х2 = -x1, х3 = 0.
Вектор у2 = (x1, -x1, 0) является решением системы, а вектор
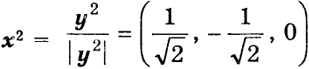
- собственный единичный вектор. Легко видеть, что он ортогонален х1 (скалярное произведение этих векторов равно нулю). Наконец, при λ3 = 1 - √3 находим, что
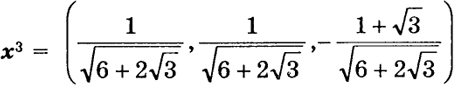
- третий собственный вектор.
Ортогональная матрица перехода от координат вектора х = (х1, х2, х3) в системе (i, j, k) к координатам вектора х = (ξ1, ξ2, ξ3) в системе (x1, х2, х3) имеет вид (см. § 17, (15))

 (6)
(6)
204
Данное преобразование сохраняет ориентацию (так как |Λ| = 1 > 0), т. е. система (х1, х2, x3) ориентирована так же, как исходная система (i, j, k).
Подставляя в нашу квадратичную форму вместо xv их значения по формулам (6), получим ее канонический вид
(1+ √3)ξ
+ (1-
√3)ξ
.
Остановимся теперь лишь на более подробном изучении уравнений и описываемых ими поверхностей, указанных выше восьми типов.
Эллипсоид
+
+
= 1 (
a, b, c, > 0) (7)
При а = b = с эллипсоид (7) обращается в сферу радиуса а с центром в начале координат, т. е. геометрическое место точек, отстоящих от начала на расстоянии а.
Величины а, b, с называются полуосями эллипсоида.
Если в уравнении (7) заменить (одновременно или порознь) х на -х, у на -у, z на -z, то оно не изменится, - это показывает, что эллипсоид (7) есть поверхность, симметричная относительно координатных плоскостей х = 0, у = 0, z = 0 и начала координат. Поэтому достаточно изучить уравнение (7) в первом октанте (системы координат), т. е. для х ≥ 0, у ≥ 0, z ≥ 0. Часть эллипсоида, находящаяся в первом октанте, определяется явным уравнением, например
z = c√1 - - , x ≥ 0, y ≥ 0,
+
≤ 1.
Для определенности будем считать, что а ≥ b ≥ с. Эллипсоид есть ограниченная поверхность. Он находится внутри шара радиуса а с центром в начале координат: для координат любой точки эллипсоида (х, у, z) имеет место неравенство
205
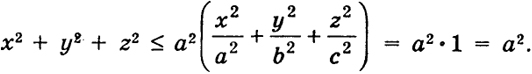
Чтобы составить более точное представление об эллипсоиде, произведем сечения плоскостями, параллельными координатным плоскостям. Например, пересекая эллипсоид плоскостями z = h(-c ≤ h ≤ с), получим в сечении эллипсы
+
= 1 -
с полуосями
a√1 - , b√1 -
Отсюда видно, что самый большой эллипс получается в сечении эллипсоида плоскостью z = 0. Аналогичная картина будет при сечении плоскостями х = h (-а ≤ h ≤ a), у = h (-b ≤ h ≤ b).
Эллипсоид (7) имеет вид, изображенный на рис. 43.
Точки (±а, 0, 0), (0, ±b, 0), (0, 0, ±с) лежат на эллипсоиде (7) и называются его вершинами.
Если какие-либо две полуоси равны между собой, то эллипсоид (7) будет эллипсоидом вращения, т. е.
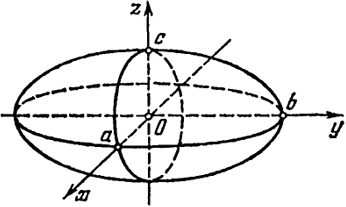
Рис. 43
206
получается от вращения эллипса относительно соответствующей оси координат.
Однополостный гиперболоид
+
-
= 1 (
a, b, c > 0) (8)
По виду уравнения (8) заключаем, что однополостный гиперболоид является поверхностью, симметричной относительно координатных плоскостей и начала координат. Числа а, b, с называются полуосями однополостного гиперболоида. Точки (±а, 0, 0), (0, ±b, 0), лежащие на поверхности (8), называются вершинами однополостного гиперболоида.
Пересечем поверхность (8) плоскостью z = h, тогда в сечении получим эллипс
+
= 1 +
с полуосями
a√1 + , b√1 + .
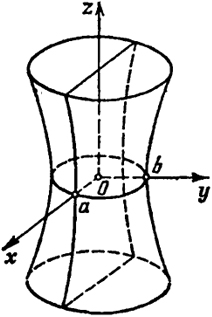
Рис. 44
207
При изменении h от -∞ до +∞ этот эллипс описывает поверхность (8).
Если теперь пересечь поверхность (8) плоскостью х = h (или у = h), то получим в сечении гиперболу
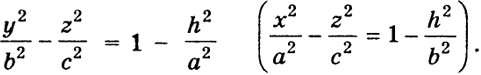
При h = ±а первая гипербола распадается на две прямые y = ±
z.
Если |h| < а, то действительной осью симметрии соответствующей гиперболы является прямая, параллельная оси Оу, а при |h| > а - прямая, параллельная оси Oz.
Действительной осью симметрии гиперболы мы называем ту из осей симметрии, которую гипербола пересекает.
Если а = b, то поверхность (8) в сечении плоскостями z = h будет иметь окружности радиуса a√1 + (h2/с2). Поверхность (8) в этом случае образуется от вращения гиперболы
-
= 1 около оси
Oz. Общий вид однополостного гиперболоида изображен на рис. 44.
Двуполостный гиперболоид
-
-
= 1 (
a, b, c > 0) (9)
Так как уравнение (9) содержит только квадраты переменных, то данная поверхность симметрична относительно плоскостей x = 0, y = 0, z = 0 и начала координат.
Уравнение (9) запишем еще в виде
208
+
= -1 +
. (9’)
Отсюда ясно, что, пересекая поверхность (9') плоскостью х = h (|h| > а), получим в сечении эллипс
+
= -1 +
с полуосями
b√(h2/a2) - 1, c√(h2/a2) - 1.
При |h| < а число (h2/а2) - 1 < 0, и поэтому нет точек пересечения поверхности (9') и плоскости х = h.
При сечении поверхности (9) плоскостями z = h (у = h) получим гиперболы
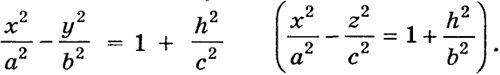
Точки (±а, 0, 0) лежат на поверхности (9) и называются вершинами двуполостного гиперболоида. Поверхность (9) изображена на рис. 45.
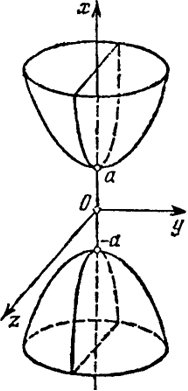
Рис. 45
209
Эллиптический параболоид
+
= 2
z (
p,
q > 0) (10)
Так как в (10) присутствуют квадраты переменных х и у, то данная поверхность симметрична относительно координатных плоскостей х = 0, у = 0. Далее, так как мы считаем р, q > 0, то поверхность (10) расположена в полупространстве z > 0.
Пересекая поверхность (10) плоскостями z = h (h ≥ 0), в сечении будем получать эллипсы
+
= 2
h
с полуосями
√2ph, √2qh.
При изменении h от нуля до ∞ данные эллипсы описывают нашу поверхность (10).
Пересекая поверхность (10) плоскостями х = h (или у = h), мы получим в сечении параболы
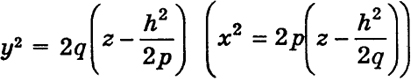
со смещенной вершиной в точке 
При р = q поверхность (10) будет поверхностью вращения, получающейся от вращения параболы х2 = 2рz около оси Oz. В этом случае поверхность (10) называют параболоидом вращения.
Точка (0, 0, 0) лежит на поверхности (10) и называется вершиной эллиптического параболоида. Эллиптический параболоид изображен на рис. 46.
210
Гиперболический параболоид
-
= 2
z (
p, q > 0) (11)
По виду уравнения (11) заключаем, что данная поверхность симметрична относительно плоскостей х = 0, у = 0. Пересекая поверхность (11) плоскостями z = h, мы будем получать в сечении гиперболы
= 2
h,
причем при h > 0 действительная ось симметрии гиперболы будет параллельной оси Оx, а при h < 0 - оси Оу. При h = 0 в сечении будут две пересекающиеся прямые.
При сечении поверхности (11) плоскостями х = h или у = h получим параболы, направленные ветвями вниз или вверх:
-
= 2
z -
,
= 2
z +
Поверхность (11) изображена на рис. 47.
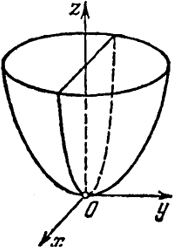
Рис. 46
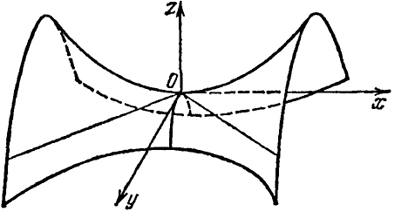
Рис. 47
211
Конус второго порядка
+
-
= 0 (
a, b, c > 0)(12)
Ясно, что данная поверхность симметрична относительно плоскостей x = 0, y = 0, z = 0и начала координат.
При сечении поверхности (12) плоскостями z = h будем получать эллипсы
+
=
.
с полуосями a|h|/c и b|h|/с.
Если же пересекать поверхность (12) плоскостями х = h или y = h, то в сечении получим гиперболы

Если теперь пересекать (12) плоскостями у = hх, то в сечении получим пару пересекающихся прямых
z = ±cx√(1/a2) + (h2/b2)
Вид конуса изображен на рис. 48.
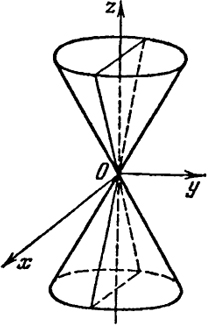
Рис. 48
212
Точка
x2 + у2 + z2 = 0. (13)
Уравнению (13) удовлетворяет только она точка х = у = z = 0.
Цилиндры второго порядка
а) Эллиптический цилиндр
+
= 1 (
a, b > 0) (14)
Уравнение (14) не содержит переменной z. На плоскости хОу уравнение (14) определяет эллипс с полуосями а и b, Если точка (х, у) лежит на этом эллипсе, то при любом z точка (х, у, z) лежит на поверхности (14). Совокупность таких точек есть поверхность, описанная прямой, параллельной оси Oz и пересекающей эллипс
+
= 1
в плоскости xOy
Эллипс (14) называют направляющей линией данной поверхности, а все возможные положения указанной движущейся прямой - образующими.
Вообще поверхность, описываемая прямой, остающейся параллельной некоторому заданному направлению и пересекающей данную линию L, называется цилиндрической. Поверхность (14) изображена на рис. 49.
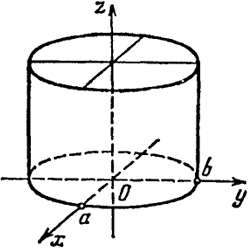
Рис. 49
213
б) Гиперболический и параболический цилиндры
-
= 1 (
a, b > 0) (15)
y2 = 2рх (р > 0). (16)
В данном случае направляющими линиями поверхностей являются гипербола и парабола, а образующими - прямые параллельные оси Oz и проходящие через гиперболу или параболу в плоскости хОу. Поверхности (15) и (16) изображены на рис. 50 и 51.
в) Параллельные и пересекающиеся плоскости. Прямая.
а2x2 - b2у2 = 0 (а, b > 0), (17)
х2 - а2 = 0 (а > 0), (18)
z2 = 0, (19)
х2 + у2 = 0. (20)
Для поверхности (17) направляющими являются прямые линии
y = ±
x.
Поэтому поверхность (17) есть пара пересекающихся плоскостей. В уравнении поверхностей (18) и (19) отсутствуют по две координаты. Уравнение (18) в плоскости хОу есть пара прямых х = ±а.
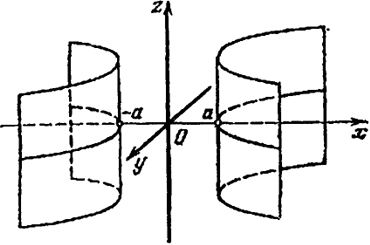
Рис. 50

Рис. 51
214
Если мы будем брать х = ±а и любые у и z, то точки (±а, у, z) будут удовлетворять уравнению (18), поэтому поверхность (18) есть пара параллельных плоскостей.
Уравнение (19) описывает плоскость хОу, так как этому уравнению удовлетворяют любые точки вида (х, у, 0), все множество которых и составляет плоскость хОу.
Можно также рассматривать г - 0 как направляющую в какой-либо из плоскостей хОz или yOz, а образующими являются прямые, параллельные оси Оу или оси Ох и проходящие через прямую z = 0.
Уравнению (20) удовлетворяет любая точка с х = у = 0 и любым z. Поэтому (20) изображает прямую, а именно, ось Oz.
Линейчатые поверхности
Некоторые поверхности второго порядка образованы движением прямой. Такими являются все цилиндрические поверхности и конус второго порядка. Однако имеются и другие поверхности, которые также образуются движением прямой.
Поверхность, образованная движением прямой, называется линейчатой, а целиком лежащие на ней прямые -прямолинейными образующими.
К линейчатым поверхностям относятся однополостный гиперболоид и гиперболический параболоид.
Уравнение однополостного гиперболоида (8) можно записать в виде
-
= 1 -
или, разлагая левую и правую части на множители, получаем
 (21)
(21)
Составим систему уравнений первой степени:
 (22)
(22)
где k - произвольный параметр.
215
При определенном значении этого параметра k мы получим прямую линию, а при изменении k - семейство прямых. Если мы перемножим уравнения (22) почленно, то получим уравнение (21) нашей поверхности. Поэтому любая точка (х, у, z), удовлетворяющая системе (22), находится на поверхности (21). Следовательно, каждая из прямых семейства (22) целиком лежит на поверхности однополостного гиперболоида.
Совершенно аналогично система
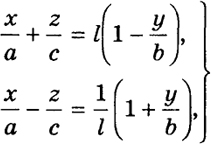 (23)
(23)
где l - параметр, также определяет семейство прямых, отличное от семейства (22), принадлежащее поверхности (21).
Через каждую точку гиперболоида (21) проходит по одной прямой каждого семейства, вообще при различных значениях параметров k и l (рис. 52). Например, через точку (√ a,
b,
c) поверхности (21) проходит прямая (22) при
k = (2 +
√6 )/(2 +
√2) и прямая (23) при
l = (2 +
√6)/(2 -
√2).
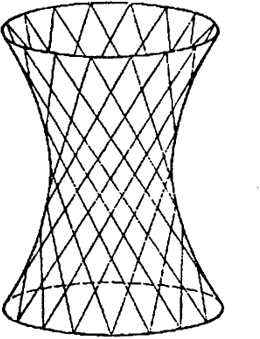
Рис. 52
216
Отметим, что однополостные гиперболоиды нашли применение в практике строительства. Сооружение различных высотных башен с использованием прямолинейных образующих однополостного гиперболоида сочетает в себе прочность конструкции с простотой ее исполнения. Идея использования однополостного гиперболоида в строительстве принадлежит нашему соотечественнику инженеру В. Г. Шухову (1853-1939). По проекту Шухова построена телевизионная башня на Шаболовке в г. Москве, она состоит из секций однополостных гиперболоидов вращения.
Легко убедиться, что два семейства прямых
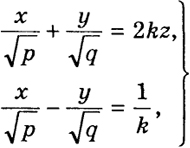 (24)
(24)
 (25)
(25)
образуют поверхность гиперболического параболоида (11).
Прямые, соответствующие семействам (24) и (25), лежат на этой поверхности и, обратно, любая точка этой поверхности есть пересечение некоторой прямой семейства (24) с некоторой прямой семейства (25).
217
