Рассмотрим плоскость R2, где задана прямоугольная система координат х1, х2. Пусть
i1 = (1, 0), i2 = (0, 1)
- орты осей x1, х2. Орты i1, i2 образуют ортонормированный базис в Rr
Произвольный единичный (нормальный) вектор b1 может быть записан следующим образом:
b1 = (cos α, sin α) (0 ≦ а < 2π).
Единичный ортогональный (перпендикулярный) к b1 вектор, который мы обозначим через b2, может соответствовать только либо углу α +
, либо α -
. Так как
141

то всевозможные ортонормированные системы b1, b2 в R2 определяются либо равенствами (рис. 35)
 (1')
(1')
соответствующими вращению осей около начала на угол а и сохранению ориентации, либо равенствами (рис. 36)
 (1'')
(1'')
соответствующими вращению осей около начала на угол а и изменению ориентации.
Оба преобразования объединяются в следующей формуле:
b1 = α11i1 + α12i2
b2 = α21i1 + α22i2 (1)
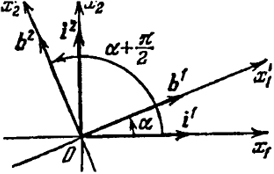
Рис. 35
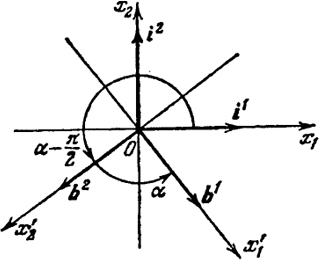
Рис. 36
142
где матрица преобразования
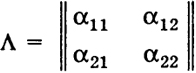 (2)
(2)
ортогональна (сумма квадратов элементов каждой из ее строк или столбцов равна 1, а скалярное произведение двух разных строк или столбцов равно 0).
Любое определенное ортогональное преобразование (1) есть на самом деле одно из преобразований (1'), (1") при некотором а.
Из (1) в силу ортогональности матрицы (2) следует, что
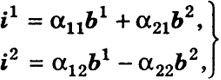 (3)
(3)
и мы получили преобразование, обратное преобразованию (1), с матрицей

сопряженной к Λ.
Зададим в плоскости произвольный вектор (точку) а. Пусть он имеет в старой и новой системе координаты (х1, х2) и (x’1, x'2). Тогда
а = x1i1 + x2i2 = x’1bl + х'2b2. (4)
В силу формул (3) и (4)
x’1b1 + x’2b2 = x1(α11b1 + α21b2) + x2(α12b1 + α22b2) =
= (α11x1 + α12x2)b1 + (α21x1 + α22x2)b2.
Поэтому, приравнивая компоненты при одинаковых ортах b1, b2, получим
 (5)
(5)
143
В силу же формул (1) и (4)
x1i1 + x2i2 = x’1(α11i1 + α11i1 + α12i2) + x’2(α21i1 + α22i2) =
= (α11x’1 + α21x’2)i1 + (α12x’1 + α22x’1 + α22x’2)i2
откуда, приравнивая компоненты при i1 и i2, получим формулы, обратные к (5):
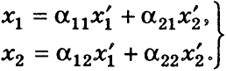 (6)
(6)
Если наряду с преобразованием (6) перенести еще начало осей x'1, x'2 в точку O’, имеющую координаты x1 = х
,
x2=
x, то формулы (6) усложнятся, очевидно, следующим образом:
 (7)
(7)
Итак, произвольное преобразование прямоугольных координат (x1, x2) в прямоугольные координаты (x’1, х'2) с переносом начала системы (х1, х2) в точку O’ = (х
,
х) выражается формулами (7), где матрица
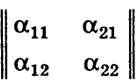
ортогональная.
Соответствующее преобразование, сохраняющее ориентацию системы координат, имеет вид
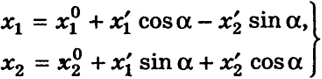 (7')
(7')
и преобразование, меняющее ориентацию, имеет вид
144
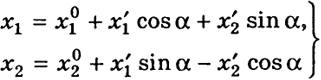 (7")
(7")
(матрицы коэффициентов при х’1 и х'2 в (7') и (7") соответственно транспонируют (1') и (1")).
145
