§ 17. Ортогональные базисы в Rn

Говорят, что два ненулевых вектора х, у ∈ R_n, имеют одинаковое (одно и то же) направление, если существует положительное число γ, такое, что х = γу.

Произвольный ненулевой вектор х ∈ R_n можно, как говорят, нормировать, заменив его на единичный вектор

y =

1

|x|

 x (|y| = 1),

имеющий то же направление, что и вектор х.

Единичный (имеющий норму (длину), равную 1) вектор называют нормальным.

Два вектора х и у в пространстве R_n называют ортогональными, если их скалярное произведение равно нулю: (х, у) = 0.

Здесь R_n может быть действительным или комплексным. В случае комплексного R_n скалярное произведение определяется, как в § 6, (5').

Система векторов

x¹, …, x_v ∈ R_n (1)

называется ортогональной, если любые два ее вектора ортогональны. Система векторов (1) называется ортогональной и нормальной или ортонормированной, если

128

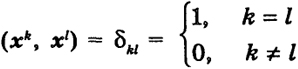
т. е. все векторы системы нормальны и попарно ортогональны. Если система векторов (1) ортогональна и ни один вектор системы не равен нулевому, то, нормируя их, получим, очевидно, ортонормированную систему. Ортонормированная система (1) линейно независима, В самом деле, пусть

γх¹ + γ₂х² + ... + γ_vx^v = 0,

где γ₁, …, γ_v - числа. Умножив это равенство скалярно на x_s, получим, очевидно,

γ_s(x_s, x^s) = γ_s = 0 (s = 1, …, v)

Но тогда ортонормированная система из п векторов в R_n есть базис и, следовательно, каждый вектор а ∈ R_n можно представить в виде линейной комбинации

a =

n

∑

k=1

 γ_kx^k (2)

Умножая это равенство скалярно на x^s, получим

(a, x^s) = γ_s (s = 1, ..., n)

и, следовательно,

a =

n

∑

k=1

 (a, x^k)x^k, ∀ a ∈R_n

Число (a, x^k) (|x^k| = 1!) называется проекцией вектора а на направление вектора x^k.

В реальном действительном пространстве R₃ величина (a, x^k) есть обычная числовая проекция вектора а на направление вектора x^k.

129

Теорема 1. Ортонормированную систему векторов

x¹, x², …, x^v (v < n)

можно пополнить до ортонормированного базиса в R_n. Иначе говоря, можно указать векторы x^v+1, ..., х^п такие, что система

x¹, …, x^v, x^v+1, …,xⁿ (3)

будет ортонормированной и, следовательно, будет базисом в R_n.

Доказательство. Так как v < n, то в R_n существует вектор а, не зависящий линейно от x¹, ..., x^v. Но тогда

a =

v

∑

k=1

 (a, x^k)x^k + y

где у ≠ 0. Вектор у ортогонален ко всем векторам x¹, ..., x^v. В самом деле,

(y, x^s) = (a -

v

∑

k=1

 (a, x^k)x^k, x^s) =
= (a, x^s) - (a, x^s) = 0 (4)

(s = 1, …, v)

Пронормировав у, получим вектор

x_v+1 =

1

|y|

 y (|x^v+1| = 1),

и система

x¹, …, x^v, x^v+1

будет ортонормирована. Если v + 1 = п, то мы получили базис в R_n. Если нет, то этот процесс продолжаем. На (п - v)-m этапе получим базис (3) в R_n.

130

Система ортов осей в R_n

i1 = (1, 0, 0, ..., 0, 0),

i2 - (0, 1, 0, ..., 0, 0),

………

in = (0, 0, 0 , ...,0, 1)

может служить примером ортонормированного базиса в R_n.

Произвольный вектор а = (x₁, ..., х_п) ∈ R_n разлагается по ортам следующим образом:

a = x₁i¹ + … + x_ni_n =

n

∑

k=1

 x_ki^k (5)

где x_k = (a, i^k) (k = 1, ..., n) - проекция вектора a на направление орта i^k.

Пусть задана некоторая определенная ортонормированная система из п векторов

(6)

или

a_k =

n

∑

s=1

 a_ksi^s (k = 1, …, n) (7)

Переход от векторов (i¹, .., iⁿ) к (a¹, ..., аⁿ) здесь осуществляется при помощи матрицы

(8)

т. е. вектор а^k выражается через i¹, ..., iⁿ с помощью k-й строки матрицы A.

131

В дальнейшем мы считаем пространство R_n и матрицу Л действительными (см. далее замечание 1).

Матрица Λ ортогональна, т. е. обладает следующим свойством:

n

∑

s=1

 a_ksa_ls = δ_kl (k, l = 1, …, n) (9)

В самом деле, так как в данном случае система а¹, ..., аⁿ ортонормирована, то

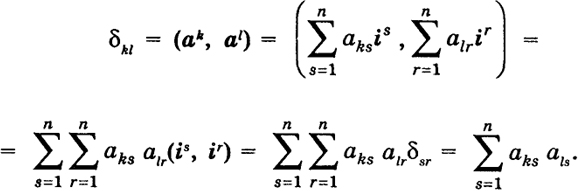(10)

Мы видим, что и, обратно, ортогональность матрицы (8) влечет за собой ортонормируемость системы векторов а¹, ..., аⁿ, определенных по формулам (7).

Это показывает, что формулы (7), где ||a_ks|| - произвольные ортогональные матрицы, определяют все возможные ортонормированные базисы в R_n.

Помножим вектор i^l на вектор а^k скалярно:

(i^l, а^k) = а_kl (11)

Отсюда

i^l =

n

∑

k=1

 (i^l, a^k)a^k =

n

∑

k=1

 a_kla^k. (12)

Таким образом, переход от базиса (а¹, ..., аⁿ) к базису (i^l, ..., iⁿ) осуществляется при помощи матрицы Λ', транспонированной к Λ. Так как преобразование (12) обратно преобразованию (7) (см. § 15), то мы попутно

132

доказали, что ортогональная матрица Л обладает следующим замечательным свойством (в действительном R_n):

Λ^-1 = Λ’. (13)

Из (12) следует

(14)

Ортогональная матрица была определена нами как такая матрица, у которой строки (векторы, представляющие их) нормальны, а разные строки ортогональны. Из этого определения, как это видно из (14), автоматически следует, что у ортогональной матрицы и столбцы нормальны, а разные столбцы ортогональны о

Переход от (x₁, ..., х_п) к (x’₁, …, х'_п) совершается при помощи матрицы, так как (считая, что

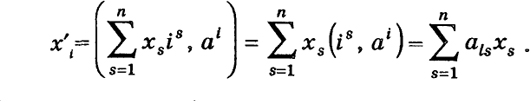
Переход же от (х’₁, ..., х'_n) к (x₁, ..., х_п) совершается при помощи (см. (13)) матрицы Λ' транспонированной к Λ, т. е.

x_s =

n

∑

l=1

  a_lsx

’

l

133

Отметим, что определитель произвольной ортогональной матрицы Л (см. (6)) по абсолютной величине равен 1: | |Λ| | - | |a_kl| | = 1.

Это следует из того, что

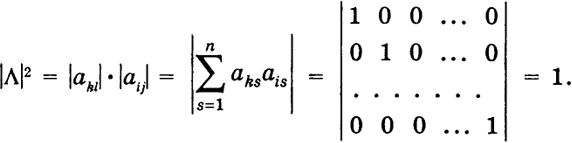
Здесь мы считаем, что элемент γ_ki. произведения определителей равен сумме произведений элементов k-й строки на соответствующие элементы i-й строки (см. § 2, свойство к)).

Отметим еще, что определитель из компонент векторов базиса i1, ..., in равен 1:

Если ортогональный базис a¹, ..., аⁿ имеет определитель |Λ| = 1 (см. (6)), то говорят, что этот базис ориентирован так же, как базис i¹, ..., iⁿ. Если же |Λ| = -1, то - противоположным образом. Эти определения согласуются с соответствующими определениями в двумерном и трехмерном случаях, сделанными в§11 и в §12.

Замечание 1. В комплексном пространстве R_n матрица (8), где a_kl комплексные, называется ортогональной, если

n

∑

s=1

 a_ksa_ls = δ_kl (k, l = 1, …, n) (9')

134

Покажем, что ортонормированная система векторов (6) в комплексном R_n порождает ортогональную матрицу Λ (см. (8)). В самом деле, в комплексном R_n скалярное произведение векторов х, у подчиняется свойствам (см. § 6, б'), в'))

(x, y) = (y, x), (αx + βy, z) = α(x, z) = α(x, z) + β(y, z)

где α, β - комплексные числа. Поэтому

(x, αy + βz) = (αy, + βz,x) = (αy,x) + (βz,x) =
= α(y,x) + β(z,x) = α (x,y) + β(x,z)

Но тогда для ортонормированной системы векторов а¹, ..., аⁿ имеет место

(10’)

т. е. матрица Λ ортогональна. Мы видим, что и, обратно, ортогональность Λ влечет ортонормированность векторов a¹, ..., аⁿ, определенных по формулам (7).

Помножим вектор i^l на а^k скалярно (см. (7)):

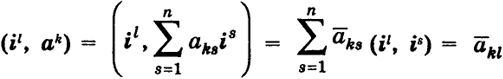
Отсюда

135

i^l =

n

∑

k=1

 (i^l, a^k)a^k =

n

∑

k=1

 a_kla^k. (12')

Таким образом, переход от базиса (a¹, ..., аⁿ) к базису (i¹, ..., iⁿ) осуществляется при помощи матрицы

Так как преобразования (11') обратны преобразованиям (7), то попутно показано, что ортогональная матрица Λ обладает следующим свойством (в комплексном R_n):

Λ^-1 = Λ*, (Λ’)^-1 = (Λ’)* = (Λ’’) = Λ. (16)

Из (12') следует

Следовательно, равенства

δ_kl =

n

∑

s=1

 a_ska_sl (k ,l = 1, …, n)

(так же, как (9’)) могут служить определением ортогональной матрицы Л.

На основании (14) и общих фактов, полученных в § 16 (петит), отметим матрицы, осуществляющие нижеследующие ортогональные отображения:

136

Λ: (i1, ..., in) → (a1, ..., an) (cm. (7));

Λ*: (a1, ..., an) → (i1, ..., in) (cm. (12'));

Λ': (x’1, ..., x’n) → (x1, ..., xn) (см. (6) § 16);

Λ: (x1, ..., xn) → (x'1, ..., x’n) (см. (16)),

где (x₁, ..., x_n) и (x'₁, ..., x'_n) - координаты произвольного вектора в комплексном пространстве R_n относительно базиса (i¹, ..., i_n) и ортонормированного базиса (а¹, ..., аⁿ).

Наконец, равенство | |Λ| | = 1 в комплексном случае доказывается так:

Ортогональные матрицы называют еще унитарными.

137