В пространстве Rn (действительном или комплексном) введем п векторов:
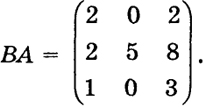 (1)
(1)
называемых ортами осей пространства Rn.
Осью xk пространства Rn называется множество точек вида (0, ..., 0, xk, 0, ..., 0), где xk стоит на k-м месте и пробегает все действительные (комплексные) значения, а вектор ik называется ортом оси xk.
Если а = (х1, ..., хп) есть произвольный вектор (действительный в действительном Rn или комплексный в комплексном Rn), то его можно, очевидно, записать в виде линейной комбинации из векторов (1) следующим образом:
а = x1i1 + x2i2 + ... + xnin (2)
122
Так как из равенства а = (x1, ..., хn) = 0 следует, что x1 = ... = хп = 0, то система (i1, ..., in) линейно независима.
Зададим произвольную систему из п линейно независимых векторов
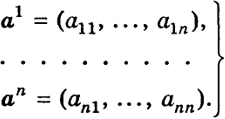 (3)
(3)
Как мы знаем (см. § 14, теорема 1), система (3) линейно независима, если определитель
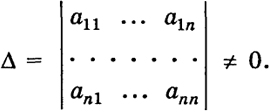 (4)
(4)
Если же А = 0, то система (3) линейно зависима.
Согласно теореме 1 § 14 любые п + 1 векторов в пространстве Rn линейно зависимы, так как ранг матрицы из компонент этих векторов не превышает п. Поэтому, если а = (x1, ..., хп) - произвольный вектор и система векторов (3) линейно независима (Δ ≠ 0), то система векторов а1, ..., аn, а линейно зависима, т. е. существуют числа γ1, ..., γn, γn+1, одновременно не равные нулю, такие, что
γ1а1 + ... + γnаn + γn+1а = 0,
где γn+1 ≠ 0 (иначе система (3) была бы линейно зависимой). Отсюда
а =
xak (5)
где x
=
(
k = 1, ...,
n). Выразим сумму (5) через орты
ik (см. (2)):
123
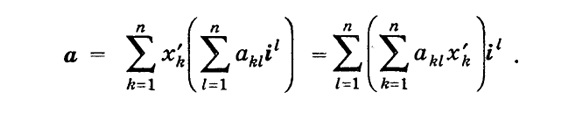
С другой стороны, по (2)
a =
xl il.
В силу линейной независимости системы i1, ..., in коэффициенты при одинаковых векторах il должны быть равны
x1 =
aklx (
l = 1, …,
n) (6)
Таким образом, если компоненты хl вектора а по системе i1, ..., in известны, то компоненты х
этого вектора по системе
а1, ...,
аn находятся из (6) и притом единственным образом, так как определитель системы (6) есть Δ ≠ 0.
Мы доказали, что, какова бы ни была линейно независимая система векторов a1, ..., аn, любой вектор а ∈ Rn можно разложить по этой системе, т. е. представить в виде суммы (5), где x
...,
х -
некоторые числа, определяемые из (6)
и притом единственным образом.
В этом смысле систему векторов а1, ..., аn называют базисом в Rn, желая этим сказать, что любой вектор а ∈ Rn можно представить в виде линейной комбинации (5) из этих векторов и притом единственным образом. Мы доказали, что произвольная линейно независимая система из п векторов в Rn есть базис в Rn.
Линейно независимая система из т векторов
| а1 = (а11, ..., a1m, al,m+l, .... aln), |
| …………………………………. |
| am = (am1,… amm, am,m+1, ..., amn), |
124
где m < n, не есть базис в Rn. В самом деле, ранг матрицы компонент этих векторов равен m. Будем считать, что первые m столбцов этой матрицы образуют определитель, не равный нулю. Расширим эту матрицу, приписав к ней внизу строку
аm+1 = (0, ..., 0, 1, 0, ..., 0),
где 1 стоит на (m + 1)-м месте. Расширенная матрица имеет ранг т + 1, и, следовательно, система векторов а1, ..., ат, аm+1 линейно независима. Но тогда вектор am+l не может быть линейной комбинацией из векторов системы a1, ..., ат, и эта система не есть базис в Rn. Обозначим через
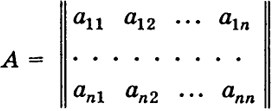
матрицу векторов (а1, ..., аn).
Переход от базиса (i1, ..., in) к базису (а1, ..., аn) осуществляется при помощи матрицы А:
ak =
aksi, (k = 1, …,
n) (7)
т. е. вектор аk выражается через векторы is с помощью k-й строки матрицы А. Обратный переход от (а1, ..., аn) к (i1, ..., in) происходит при помощи обратной матрицы А-1 (см. § 15, (9))
is =
bslal (
s = 1, …,
n) (8)
элементы которой вычисляются по формулам bsl =
, где
Аls - адъюнкт элемента
als в определителе Δ (обратим
125
внимание, что элемент bsl, принадлежащий s-й строке и l-му столбцу, выражается через адъюнкт Als элемента als, принадлежащего l-й строке и s-му столбцу). Отметим еще, что

откуда
x
=
bslxs (9)
т. е. переход от координат (x1, ,.., хп) к (х
, ...,
x) происходит при помощи матрицы (см. § 3)
(А-1)' = (А')-1.
Из (9) видно, что x
выражается через
x1, ...,
хп с помощью
l-го столбца матрицы
А-1 или
l-й строки матрицы (
А-1)', транспонированной к
А-1.
Далее по формуле (6)
xs =
alsx (
s = 1, …,
n)
видно, что переход от (х
, ...,
х) к (
х1, ...,
хп) совершается при помощи матрицы
А' транспонированной к
А, т. е.
xs выражается через
х, ...,
х с помощью
s-й строки матрицы
А' или
s-гo столбца матрицы
А.
Замечание. В § 15 было установлено, что произвольная квадратная матрица
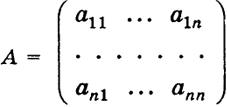 (10)
(10)
определяет линейный оператор у = Ах (х ∈ Rn, у ∈ Rn), задаваемый по формулам
126
yk =
akjxj (
k = 1, …,
n) (11)
Но имеет место и обратное утверждение: каков бы ни был линейный оператор у = Ах (х ∈ Rn, у ∈ Rn), он определяется некоторой матрицей (10) так. что вектор у = Ах вычисляется по вектору х по формулам (11).
В самом деле, пусть задан произвольный линейный оператор у = Ах (х ∈ Rn, у ∈ Rn). Обозначим образы ортов in при его помощи следующим образом:
A(is) = (a1s, a2s, …, ans) =
aksik (
s = 1, …,
n)
Тогда в силу линейности А любой вектор
x = x1i1 + … + xnin =
xsis
отображается при помощи А в вектор у, определяемый равенствами
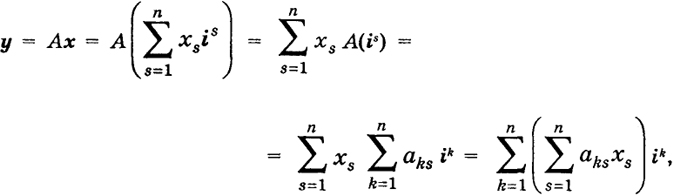
откуда следует, что k-я компонента у определяется по формуле (11). Таким образом, оператор А порождает матрицу (10), у которой в столбцах стоят координаты образов базисных векторов (ортов) при помощи оператора А.
Пример 1. Найти матрицу линейного оператора (преобразования) А, заключающегося в повороте векторов плоскости R2, выходящих из начала, на угол α (0 < α < π/2) против часовой стрелки.
127
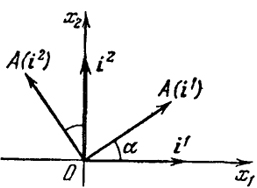
Рис. 34
Возьмем за базис векторы i1 = (1, 0), i2 = (0, 1). Тогда, очевидно, что (рис. 34)
A(il) = (cos α, sin α),
A(i2) = (-sin α, cos α).
Поэтому матрица нашего оператора имеет вид

128
