Зададим произвольную квадратную матрицу
 (1)
(1)
Матрицу А можно рассматривать как оператор, приводящий в соответствие каждому вектору х = (х1, ..., хп) ∈ Rn вектор у = (y1, ..., уп) ∈ Rn, компоненты которого вычисляются по формулам
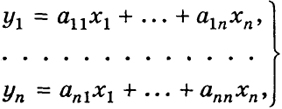 (2)
(2)
или, короче,
yi =
aij xj (
i = 1, …,
n) (2’)
Говорят, что i-я координата вектора у записывается с помощью i-й строки А. Этот оператор коротко будем записывать так:
у = Ах (х, у ∈ Rn). (2")
Замечание 1. Если аkl и далее bkl - комплексные числа, то Rn надо считать комплексным пространством. Если же akl, bkl - действительные числа, то Rn может быть и действительным и комплексным пространством.
114
В случае одномерного пространства R1 векторы х и у суть числа, и оператор (2") превращается в функцию
y = а11х.
Оператор (2") линейный. Это значит, что он удовлетворяет условию
А(αх + βx’) = αАx + βАx'
для любых векторов х, х' ∈ Rn и чисел α, β. В самом деле,
aij (α
xj + β
x) = α
aijxj + β
aijx (
i = 1, …,
n)
Если матрицы А = ||akl|| и В = ||bkl|| равны, т. е. имеют равные соответствующие элементы аkl = bkl, то они определяют тождественно равные операторы:
Ах = Вх, ∀ х ∈ Rn. (3)
Обратно, из равенства (3) вытекает, что
akl = bkl (k, l = 1, …, n)
т. е. равенство матриц А и В (А = В). В этом легко убедиться, если положить в (3)
х = x1 = (0, ..., 0, 1, 0, ..., 0),
где 1 стоит на l-м месте (l = 1, ..., п).
Таким образом, различным матрицам А соответствуют различные операторы - если две матрицы А1 и А2 отличаются хотя бы одним элементом, то обязательно существует вектор x, для которого
А1х ≠ А2х.
Пусть, кроме А, задан еще другой оператор В, определяемый квадратной матрицей n-го порядка
B = ||bkl||
115
Каждому х ∈ Rn соответствует при помощи оператора А вектор у ∈ Rn, которому при помощи оператора В соответствует вектор z с компонентами, вычисляемыми по формулам
zk =
bkiyi (
k = 1, …,
n)
В результате получим сложный линейный оператор
z = ВАх (х ∈ Rn), (4)
где
zk =
bkiyi =
bki IC
aijxj =
(
bkiaij)
xj =
γ
kjxj
с матрицей ||γkj||, называемой произведением матриц В и A. и обозначаемой так:
BA = ||γkj||, (5)
где
γkj =
bkiaij (
k,
J = 1, …,
n) (6)
т. е. чтобы получить элемент γkj. матрицы ВА (принадлежащий к ее k-й строке и j-му столбцу), надо элементы k-й строки матрицы В умножить на соответствующие элементы j-того столбца матрицы А и результат сложить.
Определитель матрицы ВА равен произведению определителей матриц В и А:
|ВА| = |В| |A| (7)
Это свойство вытекает из формулы для произведения определителей (см. § 2, свойство к)).
Пусть матрица оператора А (см. (1)) имеет определитель, не равный нулю:
116
Δ = |akl| ≠0
В этом случае (см. § 4, теорема 1) система уравнений (2), или, что все равно, операторное уравнение у = Ах имеет единственное решение х ∈ Rn при любом заданном у ∈ Rn. При этом формулы, по которым находится х для заданного у ∈ Rn, имеют вид
xj =
bjsys (
j=1, …,
n) (8)
Здесь
bjs = Аsj/Δ (s, j = 1, ..., п) (9)
(см. § 4, (3')), где Аsj - алгебраическое дополнение элемента аsj в определителе Δ.
Впрочем, для нас сейчас важно только отметить, что числа bjs являются элементами матрицы
B = ||bjs||,
обладающей следующими замечательными свойствами:
ВАх = х ∀x ∈ Rn, (10)
АВу = у ∀ y ∈ Rn. (11)
В самом деле, произвольный вектор х ∈ Rn переходит посредством оператора А в некоторый вектор у, который переходит посредством оператора B обратно в х. С другой стороны, каждому у ∈ Rn соответствует при помощи оператора В (см. (8)) некоторый х и притом такой, что Ах = у.
В равенстве (11) можно, очевидно, вместо у поставить другую букву, поэтому мы получили тождества
ВАх = АВх = х, ∀х.
Оператор х = Еx: ( ∀x ∈ Rn) называется единичным оператором. Матрица, ему соответствующая, имеет вид
117

и называется единичной. Мы доказали, что
АВ = ВА = Е.
Оператор В, обладающий этим свойством, называется обратным к оператору А и обозначается через А-1. Соответственно его матрица называется обратной матрицей к матрице А и обозначается тоже через А-1. Элементы матрицы А-1 находятся по элементам матрицы А с помощью формул (9).
Мы доказали, что если определитель |А| квадратной матрицы А не равен нулю, то она имеет обратную матрицу А-1. Для А-1, таким образом, выполняются свойства
А-1 А = АА-1 = Е.
Если определитель матрицы А равен нулю (|A| = 0), то она не имеет обратной матрицы. Достаточно сказать, что уравнение у = Ах имеет решение не для всякого у. Между тем свойство АА-1у = у, если оно выполняется, утверждает, что каждому у ∈ Rn соответствует (при помощи оператора А-1) такой х, что он есть решение уравнения у = Ах.
Замечание. Операцию умножения матриц можно распространить и на неквадратные матрицы B и А, лишь бы число столбцов матрицы В совпадало с числом строк матрицы А. Тогда умножение матриц производим по формулам, подобным (6). Например, если
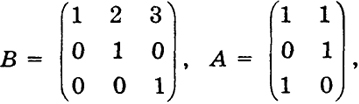
118
Произведение АВ в данном случае рассматривать нельзя, так как у матрицы А два столбца, а у матрицы В три строки.
Для квадратных матриц А и В произведения АВ и ВА имеют смысл, но далеко не всегда АВ равно ВА. Например, если
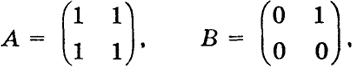
то
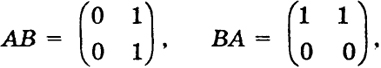
т. е. АВ ≠ ВА.
Легко проверить, что (АВ)С = А(ВС).
Если А - линейный оператор, то запись Ах можно рассматривать как произведение матрицы А на одностолбцовую матрицу
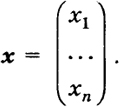
Пусть заданы линейные операторы А и В. Суммой их называется оператор А + В, определяемый равенством
(А + В)х = Ах + Вх ∀ х ∈ Rn.
Очевидно, матрица оператора А + В совпадает с матрицей, равной сумме матриц операторов А и В.
Легко проверить, что
А(В + С) = АВ + АС.
Пример 1. Найти матрицу,.обратную матрице
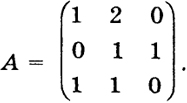
119
Матрица А определяет линейный оператор у = Ах, приводящий в соответствие каждому вектору х = (х1, х2, х3) вектор у = (г/,, у," у3) при помощи равенств
y1 = x1 + 2x2,
y2 = Х2 + x3,
y3 = x1 + 2x2,
Эти равенства можно рассматривать также как линейную систему трех уравнений относительно неизвестных x1, x2, х3. Определитель этой системы не равен нулю. Но тогда ее можно решить при любых заданных y1, y2, y3. В результате получим равенства
x1 = -y1 + 2y3,
x2 = y1 - y3,
x3 = -y1 + y2 + y3,
определяющие оператор х = А-1у, обратный к оператору А. Матрица этого оператора
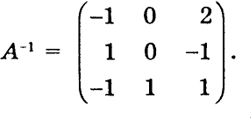
Это и есть матрица, обратная к матрице А.
Элементы матрицы А-1 можно получить путем вычислений по формулам (9).
Обозначим элементы обратной матрицы А-1 через bjs. Имеем Δ = 1, bjs = Asj,
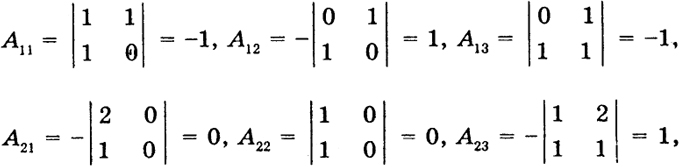
120

Таким образом,
| b11 = A11 = -l, |
b12 = A21 = 0, |
b13 = A31 = 2, |
| b21 = A12 = 1, |
b22 = A22 = 0, |
b23 = A32 = -1, |
| b31 = A13 = -1, |
b32 = A23 = 1, |
b33 = A33 = 1. |
Итак,

Пример 2. Вычислить произведение матриц ВА, где
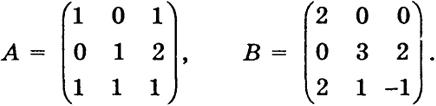
Вычисление можно произвести по формулам (5), (6), но можно рассуждать и следующим образом.
Матрица А определяет оператор у = Ах, приводящий в соответствие векторам х = (x1, х2, х3) векторы у = (у1, у2, у3) при помощи равенств
y1 = х1 + х3,
y2 = Х2 + 2Х3,
yз = Х1 + Х2 + Х3.
Матрица же В определяет оператор z = By, приводящий в соответствие векторам у = (y1, y2, у3) векторы z = (z1, z2, z3) при помощи равенств
z1 = 2у1,
z2 = 3y2 + 2у3,
z3 = 2y1 + y2 - yЗ.
121
Но тогда оператор
z = ВАх
определяется равенствами
| z1 = 2(xl + x2) |
= 2x1 |
+ 2x3, |
| z2 = 3(x2 + 2x3) + 2(xl + x2 + x3) |
= 2x1 + 5x2 |
+ 8x3, |
| z3 = 2(x1 + x2) + (x2 + 2x3) - (x1 + x2+ x3) |
= x1 |
+ 3x3. |
Следовательно, произведение ВА матриц В и А есть матрица
122
