Векторно-скалярным (смешанным) произведением векторов а, b, с (в трехмерном действительном пространстве) называется скаляр, равный скалярному произведению вектора а × b на вектор с:
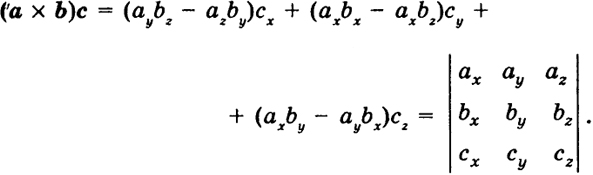 (1)
(1)
В силу определения скалярного произведения
(a × b)с = |а × b|пpa×b c = (|a| |b|sin ω)прa×bс.
Поэтому можно еще, очевидно, сказать, что смешанное произведение (а × b)с равно объему параллелепипеда, построенного на векторах а, b, с со знаком + или - в зависимости от того, будет ли система векторов а, b, с ориентирована как система координат х, у, z или противоположным образом. Отметим, что |прa×bс| равна высоте параллелепипеда.
Имеют место равенства
(а × b)с = (с × а)b = (b × с)а, (2)
которые легко следуют из свойств определителя (1).
104
Если векторы а, b, с лежат в одной плоскости, то
(а × b)с = 0,
так как a × b перпендикулярен вектору с. Обратно, если (а × b)с = 0, то вектор с перпендикулярен вектору а × b и, следовательно, лежит в плоскости векторов а и b или в плоскости, параллельной этой плоскости.
Таким образом, условие
(а × b)с = 0
есть необходимое и достаточное условие компланарности трех векторов а, b, с.
Пример 1. Найти условие принадлежности четырех точек к одной плоскости.
Пусть даны четыре точки Aj = (xj, yj, zj) (j = 1, 2, 3, 4). Если эти точки лежат в одной плоскости, то векторы
,
,
также лежат в этой плоскости, и, следовательно, их смешанное произведение равно нулю:
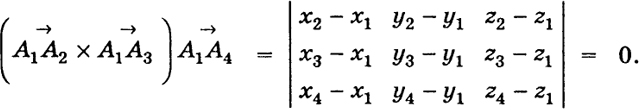
Это и есть условие принадлежности четырех точек одной плоскости (ср. § 9, (12)).
105
