11.1. Двумерная система координат. На рис. 24 и 25 изображены системы координат х, у. Они различны - про них говорят, что они ориентированы противоположно. В случае рис. 24 поворотом оси х вокруг точки О
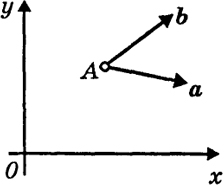
Рис. 24
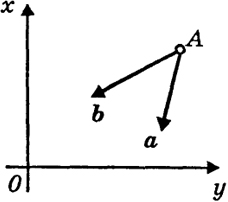
Рис. 25
на угол π/2 можно совместить направление осей х и у, лишь если этот поворот совершить против часовой стрелки. В случае же рис. 25 этой цели можно достичь, лишь поворачивая ось х по часовой стрелке. Невозможно систему координат, изображенную на рис. 24, передвигая ее в рассматриваемой плоскости (!) как твердое тело,
93
совместить с системой, изображенной на рис. 25, так, чтобы направления соответствующих осей совпали.
На рис. 24, так же как на рис. 25, изображена пара неколлинеарных, выходящих из некоторой точки А векторов а и b. Передвигая эту пару как твердое тело в плоскости, достигнем того, чтобы точка А совпала с началом координат О. Поставим себе задачу путем вращения каждого из векторов а и b вокруг точки О достигнуть того, чтобы вектор а принял направление оси х, а вектор b оказался лежащим на оси у. При этом мы требуем, чтобы во время этого процесса векторы а и b все время находились в рассматриваемой плоскости и чтобы угол между ними не был равен 0 и π. Очевидно, всегда можно достигнуть этой цели. Вначале мы вращаем систему векторов а и b как твердое тело около точки О до совпадения вектора а с положительным направлением оси х. Так как векторы а и b не коллинеарны, то вектор b окажется в верхней или нижней полуплоскости. Затем вектор b поворачиваем на необходимый угол, чтобы он оказался на оси у, при этом не разрешается, чтобы вектор b попадал на ось х. Поэтому может случиться, что направление вектора b совпадает с направлением оси у (это возможно, когда вектор b был в верхней полуплоскости) или же вектор b окажется направленным в сторону отрицательного
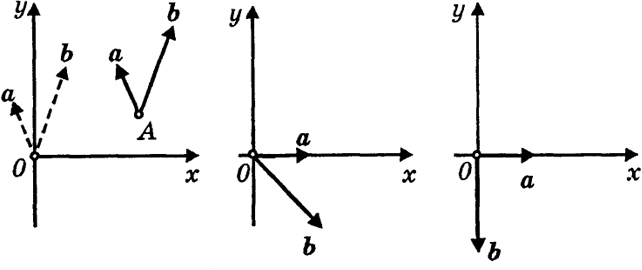
Рис. 26
94
направления оси у (см. рис. 26, где показана динамика процесса). В первом случае мы будем говорить, что пара векторов (а, b) ориентирована как система координат х, у, а во втором, что пара (а, b) ориентирована противоположно ориентации х, у (как это случилось на рис. 26).
11.2. Трехмерная система координат. Прямоугольные системы координат х, у, z в пространстве, изображенные на рис. 27 и 28, тоже различны. Рассматривая систему координат рис. 27 как твердое тело, можно после соответствующего его передвижения совместить оси х и у обеих систем координат. Но положительное направление оси 2 первой системы не совпадает с положительным направлением оси z второй системы. Мы говорим, что
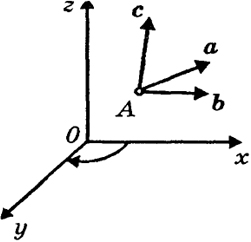
Рис. 27
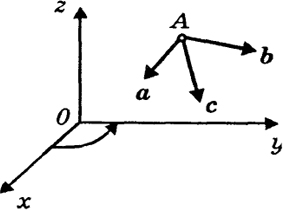
Рис. 28
системы рис. 27 и 28 ориентированы противоположно. Система рис. 27 называется левой системой координат, а система рис. 28 - правой системой координат. Если винт с правой (левой) нарезкой ввинчивать по направлению оси z, поворачивая его по стрелке рис. 28 (рис. 27), то он будет двигаться поступательно в этом направлении. Можно также распознавать систему координат по следующему правилу. Если смотреть из какой-либо точки положительной полуоси Oz на положительную полуось Оу, то положительная полуось Ох может быть направлена влево или
95
вправо. В первом случае система координат называется левой (рис. 27), а во втором - правой, (рис. 28).
Векторы а, b, с называются компланарными, если они лежат в одной плоскости или же находятся в параллельных плоскостях.
Возьмем систему некомпланарных векторов а, b, с, приложенных к некоторой точке А. Будем вращать в плоскости векторов а и b вектор b вокруг точки А до тех пор, пока b не окажется перпендикулярным а. Во время движения будем следить, чтобы угол между а и b все время не равнялся нулю и π. После этого будем вращать вектор с около А с целью придать ему направление, перпендикулярное векторам а, b. При этом будем следить за тем, чтобы вектор с ни на один момент не совпал с плоскостью векторов а и b. В результате векторы а, b, с окажутся перпендикулярными. Теперь перенесем эту тройку как твердое тело в точку О и будем ее вращать вокруг точки О с целью, чтобы векторы a и b получили соответственно направления осей х, у. Может оказаться два случая: 1) вектор с будет направлен как положительная ось z, 2) он будет направлен в противоположную сторону. В первом случае будем говорить, что система векторов а, b, с ориентирована как система координат х, у, z, а во втором - она ориентирована противоположным образом (см. соответственно рис. 27 и 28).
96
