10.1. Уравнение прямой в каноническом виде. Рассмотрим в пространстве произвольную прямую L. Отметим на ней точку (x0, y0, z0), определяющую радиус, вектор ρ0 = (х0, у0, z0) и лежащий на ней вектор а = (a1, а2, а3) ≠ 0, приложенный к точке Q0 = (x0, y0, z0) (Рис. 23). Произвольную текущую точку прямой L обозначим через Q = (x, y, z) и ее радиус-вектор через ρ = (х, у, z) Вектор ρ - ρ0 можно записать в виде ρ - ρ0 = ta, где t - некоторое число (скаляр). Если действительная переменная t пробегает интервал (-∞, ∞), то конец вектора ρ = ρ0 + ta пробегает всю прямую L. Поэтому говорят, что равенство
ρ - ρ0 = ta (-∞ < t < ∞) (1)
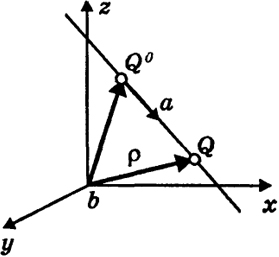
Рис. 23
89
есть уравнение прямой, проходящей через точку Q0 = (х0, y0, z0) и направленной в сторону вектора а.
На языке координат уравнение (1) распадается на три уравнения:
 (1’)
(1’)
Исключая из них параметр t, получим уравнения прямой (систему из двух уравнений)
=
(1’’)
где числа а1 а2, а3 одновременно не равны нулю. Уравнения (1") называются уравнениями прямой в каноническом виде.
Замечание. Может случиться, что одно или два из чисел а1, а2, а3 равно нулю. Тогда все же принято писать равенства (1") с нулем или двумя нулями в знаменателях. Такая запись становится тогда символической, но она удобна.
Пример 1. Уравнения
=
=
(2)
определяют прямую в пространстве, проходящую через точку (1, 2, 3) в направлении вектора (1, 0, 2).
Эти уравнения можно заменить на следующие им эквивалентные:
у - 2 = 0 ∙ (х - 1), 2(х - 1) = z - 3,
т. е.
у = 2, z = 2х + 1. (2Л)
90
Таким образом, рассматриваемая прямая есть пересечение двух плоскостей, определяемых уравнениями (2').
Пример 2. Уравнения прямой
=
=
эквивалентны следующим:
у - 2 = 0, z - 3 = 0.
10.2. Расположение двух плоскостей. Пусть заданы уравнения двух плоскостей
Ах + By + Cz + D = О, (3)
А'х + Е'у + C'z + D' = 0. (4)
Если коэффициенты первого из них соответственно пропорциональны коэффициентам второго (А : В : С = А' : В’ : С'), то плоскости (3) и (4) параллельны или даже совпадают (при условии А : В : С : D = А' : В' : С' : D') (см. § 9, (17) и (18)). В противном случае плоскости (3) и (4) пересекаются по прямой. В этом случае один из определителей
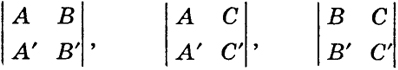
не равен нулю. Для определенности будем считать, что первый
 (5)
(5)
Тогда уравнения (3), (4) можно решить относительно х и y, и мы получим
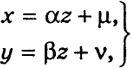 (6)
(6)
91
где α, β, μ, ν - некоторые числа. Уравнения (6) эквивалентны следующим:
=
=
(7)
Мы видим, что при условии (5) уравнения двух плоскостей (3), (4) определяют прямую (7), т. е. геометрическое место точек, координаты которых удовлетворяют уравнениям (3), (4). Она проходит через точку (μ, ν, 0) и имеет направление вектора (α, β, 1). Числа а, р или одно из них могут быть равными нулю, тогда уравнения (7) будут иметь символический характер.
Пример 3. Прямая, определяемая уравнениями х = 0, у = 0, есть, очевидно, координатная ось z. К этому результату можно прийти и формально. Имеем
х = 0 ∙ z, у = 0 ∙ z,
откуда
=
=
т. е. мы получили уравнения прямой, проходящей через начало координат (0, 0, 0) в направлении вектора (О, О, 1). Ясно, что эта прямая есть ось z.
Пример 4. Найти угол между прямыми
=
=
(8)
=
=
(9)
Векторы r1 = (a1, b1, c1), r2 = (а2, b2, с2) лежат на наших прямых и, как мы условились, они приложены соответственно к точкам (x1, y1, z1), (x2, y2, z2). Поэтому угол φ
92
между этими векторами и будет углом между прямыми (8) и (9):
cos φ =
- Написать уравнение прямой, проходящей через точку (2, -1, 0) перпендикулярно к плоскости 2х + z - 4у = 7.
- Написать уравнение плоскости, проходящей через точку (1, -1, 2) и перпендикулярной к прямой, определяемой уравнениями 2х + 3у - 1, 3х - z = 1.
93
