9.1. Уравнение плоскости в нормальном виде. В пространстве Д3, где введена прямоугольная система координат х, у, z, зададим вектор а, выпущенный из начала О. Через конец а проведем плоскость П перпендикулярно к а (рис. 20). Произвольную (текущую) точку плоскости П обозначим через Q = (x, у, z). Буква ρ обозначает радиус-вектор точки Q.
Пусть р = |а| - длина вектора а и
v = (cos a, cos Р, cos у)
- единичный вектор, направленный в ту же сторону, что и а. Здесь α, β, γ - углы, образуемые вектором v соответственно с положительными направлениями осей x, y, z. Проекция любой точки Q ∈ П на вектор v есть, очевидно, величина постоянная, равная р:
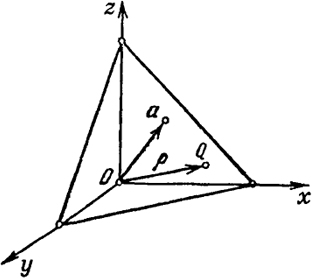
Рис. 20
(ρ, ν) = р (р ≥ 0). (1)
Уравнение (1) имеет смысл и при р = 0. В этом случае плоскость П проходит через начало координат О (а = 0) и v - единичный вектор, выпущенный из О перпендикулярно к П, неважно в каком направлении, т. е. вектор v определяется с точностью до знака. Уравнение (1) есть уравнение плоскости П в векторной форме. В координатах оно записывается так:
80
xcos α + ycos β + zcos γ = p (p ≥ 0) (1')
и называется уравнением плоскости в нормальном виде.
9.2. Уравнение плоскости в общем виде. Если уравнение (1') умножить на какое-либо не равное нулю число, то получим эквивалентное ему уравнение в виде
Ах + By + Cz + D = 0, (2)
определяющее ту же плоскость. Здесь числа А, В, С не равны нулю одновременно. Уравнение (2), где числа А, В, С не все равны нулю, называется уравнением плоскости в общем виде.
Произвольное уравнение вида (2), где числа А, В, С одновременно не равны нулю, можно привести к нормальному виду, умножив его на число
М = ±1/ √А2 +В2 +С2,
где знак берется противоположным знаку числа D. Тогда число p = -MD будет неотрицательным, а уравнение (2) преобразуется в следующее, ему эквивалентное,
МАх + МВу + MCz = р (р ≥ 0). (3)
Здесь
(MA)2 + (MB)2 + (MC)2 = 1.
Это показывает, что вектор
ν = (МA, MB, МС)
единичный (|ν| = 1). Его проекции на оси координат равны
MA = cos α, MB = cos β, МС = cos γ,
где α, β, γ - углы, образованные вектором v соответственно с положительными направлениями осей х, у, z. В силу введенных обозначений уравнение (3) имеет вид
81
xcos α + ycos β + zcos γ = p (p ≥ 0), (3')
т. е. мы получили уравнение плоскости (2) в нормальном виде.
Если задано уравнение плоскости в общем виде (2) и надо узнать ее расположение относительно системы координат, то достаточно уравнение (2) привести к нормальному виду, умножив его на нормирующий множитель М.
Из самого же уравнения (2) без каких-либо вычислений можно заключить только следующие два факта: 1) если D = О, то плоскость проходит через начало координат, а если D ≠ 0, то она не проходит через начало координат; 2) вектор N = (А, В, С) перпендикулярен плоскости, ведь он коллинеарен единичному вектору ν = (MA, MB, MC) = MN, перпендикулярному к данной плоскости.
Уравнение
Ах + By + D = 0 (4)
есть частный случай уравнения (2). В плоскости (х, у) уравнение (4) определяет прямую, а в пространстве (х, у, z) оно есть уравнение плоскости П, перпендикулярной к координатной плоскости (х, у) и проходящей через эту прямую. Какова бы ни была точка (х, у, z), принадлежащая к плоскости П, ее координаты х, у удовлетворяют уравнению (4) независимо от того, какую она имеет третью координату z. Уравнение
Ах + D = 0 (А ≠ 0) (5)
есть частный случай уравнения (4). Его можно записать еще в виде
х = С (С = -D/A). (5')
Уравнение (5') в пространстве (х, у, z) есть геометрическое место точек (х, у, z), имеющих первую координату, равную числу С. Координаты же yt z могут быть
82
любыми. Ясно, что (5') определяет плоскость, параллельную координатной плоскости (у, z) (или перпендикулярную оси х).
9.3. Уравнение плоскости в отрезках. Если числа А, В, С, D не равны нулю, то уравнение (2) можно записать так:
+
+
= 1, (6)

Рис. 21
где а = -D/A, b = -D/B, с = -D/C.
Уравнение (6) называется уравнением плоскости в отрезках. Эта плоскость (рис. 21) пересекает ось х в точке (а, 0, 0), ось у -в точке (0, b, 0), ось z - в точке (0, 0, с). По уравнению (6) легко представить себе расположение плоскости относительно системы координат.
9.4. Уравнение плоскости, проходящей через точку. Если точка (х0, у0, z0) лежит на плоскости (2), то ее координаты удовлетворяют уравнению (2):
Ах0 + Ву0 + Cz0 + D = 0. (7)
Вычитая (7) из (2), получим
А(х - х0) + В(у - y0) + C(z - z0) = 0. (8)
Уравнение (8) называется уравнением плоскости, проходящей через точку (х0, у0, z0). В векторной форме уравнение (8) имеет вид
N(ρ - ρ0) (8')
где N, ρ, ρ0 - векторы, определяемые равенствами
N - (А, В, С), ρ = (х, у, z) ρ0 = (x0, y0, z0).
83
Здесь N - вектор, перпендикулярный к плоскости (2), ρ - радиус-вектор текущей ее точки, ρ0 - радиус-вектор заданной ее точки. Так как вектор ρ - ρ0, приложенный к точке (х0, у0, z0), принадлежит плоскости (2), то равенство (8) говорит о том, что вектор N ортогонален плоскости (2), что мы установили ранее из других соображений.
9.5. Уравнение плоскости, проходящей через три точки. Даны три точки
(x1, y1, z1), (x2, y2, z2), (x3, y3, z3)
не лежащие на одной прямой. Требуется написать уравнение плоскости, проходящей через эти три точки. Из геометрии известно, что такая плоскость существует и единственная. Так как она проходит через точку (x1, y1, z1) то ее уравнение имеет вид
А(х - x1) + В(у - y1) + C(z - z1) = 0, (9)
где А, В, С одновременно не равны нулю. Так как она проходит еще через точки (х2, у2, z2), (x3, у3, z3), то должны выполняться условия
 (10)
(10)
Составим однородную линейную систему уравнений относительно неизвестных и, v, w:
 (11)
(11)
Здесь (х, у, z) есть произвольная точка, удовлетворяющая уравнению плоскости (9). В силу (9) и (10) системе (11) удовлетворяет нетривиальный вектор N = (А, В, С), поэтому определитель этой системы равен нулю
84
 (12)
(12)
Мы получили уравнение вида (9), т. е. уравнение плоскости, в чем легко убедиться, разложив полученный определитель по элементам первой строки. При этом эта плоскость проходит через точки (x1 y1, z1), (x2, y2, z2), (x3, у3, z3), что вытекает из свойств определителя. Наша задача решена. Уравнение (12) можно еще написать и в следующем виде:
 (13)
(13)
Если из первой, третьей и четвертой строк определителя в (13) вычесть вторую строку, то он не изменится. Разлагая результат по элементам четвертого столбца, получим уравнение (12).
9.6. Угол между двумя плоскостями. Зададим две плоскости
Ах + By + Cz + D = 0, (14)
А'х + В'у + C'z + D' = 0.
Мы знаем, что векторы N = (А, В, С) и N' = (А', В', С') перпендикулярны соответственно данным плоскостям, поэтому угол φ между N и N' равен углу (двугранному) между данными плоскостями. Но скалярное произведение
NN' = |N||N’| соs φ,
85
поэтому
cos φ =
=
. (15)
Достаточно считать, что 0 ≤ φ ≤ π.
Отметим, что две пересекающиеся плоскости на самом деле образуют два двугранных угла φ1 и φ2. Их сумма равна π (φ1 + φ2 = π), а их косинусы равны по абсолютной величине, но отличаются знаками (cos φ1 = -cos φ2). Если заменить в первом уравнении (14) числа А, В, С соответственно на числа -А, -В, -С, то полученное уравнение будет определять ту же плоскость, но угол φ в (15) заменится на π - φ.
Две плоскости (14) перпендикулярны тогда и только тогда, когда cos ф = 0, т. е.
NN' = АА' + ВВ' + СС' = 0 (16)
Две плоскости (14) параллельны тогда и только тогда, когда (перпендикулярные к ним) векторы N и N' коллинеарны, т. е. выполняются условия пропорциональности
=
=
(17)
Если дополнительно к этому выполняются расширенные условия пропорциональности
=
=
=
(18)
то это говорит о том, что плоскости (14) совпадают, т. е. оба уравнения (14) определяют одну и ту же плоскость. Хотя на нуль делить нельзя, но удобно писать символические пропорции (17) или (18) с нулями в знаменателях. Но тогда, если, например, В’ = 0, то надо считать, что и В = 0. Или если D' = 0, то D = 0.
86
Пример 1. Уравнения
2х + 4у + 1 = 0,
х + 2у + 5 = 0
определяют пару параллельных плоскостей, а уравнения
2х + 4y + 2 = 0,
х + 2у + 1 = 0
- пару совпадающих плоскостей.
9.7. Расстояние от точки до плоскости. Требуется найти расстояние от точки (х0, у0, z0) = Q0 до плоскости П, определяемой уравнением
Ах + By + Cz + D = 0.
Для этого приведем уравнение П к нормальному виду:
(ρ, ν) = р (р ≥ 0).
Здесь ρ = (х, у, z) - радиус-вектор текущей точки Q плоскости П, р - длина перпендикуляра а к П, выпущенного из нулевой точки, и ν - единичный вектор, направленный как а. Из рис. 22 видно, что разность ρ - ρ0 радиус-вектора произвольной точки Q = (х, у, z) плоскости П и

Рис. 22
87
радиус-вектора точки Q0= (x0, y0, z0) есть такой вектор, что абсолютная величина его проекции на ν равна искомому расстоянию d от Q0 = (x0, у0, z0) до П:
d = |(ρ - ρ0, ν) - p|
но
(ρ - ρ0, ν) = (ρ, ν) - (ρ0, ν) = p - (ρ0, γ)
Следовательно,
d = |(ρ0, ν) - р|.
Мы видим, что, для того чтобы вычислить расстояние d от точки Q0 до плоскости П, надо записать уравнение плоскости П в нормальном виде, перенести р в левую часть и подставить в последнюю (x0, y0, z0) вместо (х, у, z).
Абсолютная величина полученного выражения и есть искомое число d.
На языке параметров плоскости, очевидно,
d = |Ах0 + Ву0 + Cz0 + D|/ √A2 + B2+C2 .
Легко видеть, что если точка Q0 и начало координат находятся по разные стороны от плоскости П (как на рис. 22), то вектор ρ - ρ0 образует с ν тупой угол, и поэтому
d = -(ρ - ρ0, ν) = (ρ0, ν) - р > 0.
Если же точка Q0 и начало координат находятся по одну сторону от П, то указанный угол острый, и тогда
d = (ρ - ρ0, ν) = р - (ρ0, ν) > 0.
Следовательно, в первом случае (ρ0, ν) > р, а во втором (ρ0, ν) < р.
Пример 2. Расстояние d от точки (1, 1, 1) до плоскости П
х + 2у + z = 3
равно
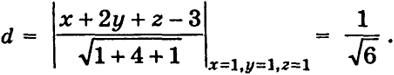
88
В данном случае точка (1, 1, 1) и начало координат находятся по разные стороны от плоскости П, так как М > 0 и
[х + 2у + z - 3]x=1, y=1, z=1 = 1 > 0.
ЗАДАЧИ
1. Привести уравнения плоскостей
х - у + z = 2, 2х - у + √20 z = 10
к нормальному виду.
2. Найти угол между плоскостями
x + y + z = 1 и y = 0
x - y + z = 2 и x + y + z = 3
3. Написать уравнение плоскости, проходящей через точки (0, 0, 1), (1, 0, 1), (1, 1, 0).
4. Написать уравнение шаровой поверхности с центром в начале координат, касающейся плоскости 2х - 6у + 7z = 2.
89
