До анализа и интерпретации количественных данных, полученных в результате проведенных диагностических процедур, необходимо их обобщить. В таблице 2 приводятся результаты тестирования знаний учащихся по определенному учебному предмету. Отметки в баллах проставлялись в алфавитном порядке так, как записаны в классном журнале. Однако в подобной форме представление результатов тестирования не слишком удобно для анализа. Поэтому необходимо эти данные представить так, чтобы можно было проследить определенную логику и закономерность как в числовом ряде, так и в процессе усвоения знаний учащимися. Для этого в прикладной математической диагностике существуют четко разработанные правила обработки и представления конечного результата.
Таблица 2
Результаты тестирования знаний учащихся по математике
| № п/п |
Учащийся |
Оценка |
|
№ п/п |
Учащийся |
Оценка |
| 1 |
Андреев И. |
90 |
|
20 |
Лаврентьева Ю. |
80 |
| 2 |
Авдеева О. |
66 |
|
21 |
Леонтьев С. |
75 |
| 3 |
Афанасьев Н. |
106 |
|
22 |
Левшов Д. |
75 |
| 4 |
Борисов Ю. |
84 |
|
23 |
Максимов Ю. |
51 |
| 5 |
Баринова Н. |
105 |
|
24 |
Минашкина Е. |
109 |
| 6 |
Ворошилов А. |
83 |
|
25 |
Музыкова Л. |
89 |
| 7 |
Володин Е. |
104 |
|
26 |
Николаев В. |
58 |
| 8 |
Викторова Е. |
82 |
|
27 |
Орлова Н. |
59 |
| 9 |
Владимирова С. |
97 |
|
28 |
Петрова З. |
72 |
| 10 |
Гаврилов Н. |
97 |
|
29 |
Потапов Д. |
74 |
| 11 |
Гончарова Ф. |
59 |
|
30 |
Романова Е. |
75 |
| 12 |
Головина С. |
95 |
|
31 |
Смирнов В. |
81 |
| 13 |
Данилов М. |
78 |
|
32 |
Столяров Ю. |
71 |
| 14 |
Дмитриева Н. |
70 |
|
33 |
Тихонова Л. |
68 |
| 15 |
Ершов И. |
47 |
|
34 |
Шашков И. |
112 |
| 16 |
Емельянова Е. |
95 |
|
35 |
Юнусова Т. |
62 |
| 17 |
Иванов Ю. |
100 |
|
36 |
Юлдашев Г. |
91 |
| 18 |
Казаков К. |
69 |
|
37 |
Яковлева Л. |
93 |
| 19 |
Костина Е. |
44 |
|
38 |
Яковлев Д. |
84 |
70
Первый этап представления данных - это их ранжирование, т.е. упорядочивание оценок по величине от максимальной до минимальной. В таблице 3 рассматриваются те же оценки 38 учеников, что и в таблице 2, но упорядоченные по убыванию от 112 (самого высшего) до 44 (низшего). Теперь будет нетрудно заметить, кто из учеников какой ранг занимает. Но, вероятно, могут иметь место и равные оценки, в особенности при сопоставлении учащихся нескольких классов. Так, в нашем примере два ученика получили по 97 очков. Поскольку в данном случае нельзя утверждать, что один ранг выше другого, мы обязаны приписать им одинаковые ранги. Так как существует шесть учеников, ранг которых выше (1, 2, 3, 4, 5, 6), то следующие два ранга, 7 и 8, усредняются, что дает 7,5. Точно так же среднее рангов 9 и 10 составит 9,5 и т.д. Есть три ученика с оценкой 75 и 21 ученик, ранг которых выше; среднее следующих трех рангов (22, 23 и 24) равно 23, что дает ранг для каждой оценки 75. Кроме того, для определения рангов требуется много времени и сил, список получается длинным, громоздким и неудобным для сравнения с другими классами, большими или меньшими: ранг 19 в классе из 38 учеников будет хуже, чем в классе с бо́льшим числом учащихся.
Второй этап - выявление распределения частот. Этот список можно сократить, классифицируя оценки по распределению частот, иногда называемому просто распределением. Третий и четвертый столбцы таблицы 3 показывают простейший вид распределения. Различные оценки размещаются по величине, в данном случае от 112 до 44, а справа от каждой оценки указывается число ее повторений. Каждое число справа называется частотой и обозначается f а сумма частот обозначается п.
Третий этап- распределение сгруппированных частот. Для большого числа оценок - скажем 100 или более - на следующем этапе может иметь смысл обобщение данных. Как правило, существует настолько широкий диапазон оценок, что целесообразнее сгруппировать их по величинам, например в группы, объединяющие все оценки от 105 до 109 включительно, от 110 до 114 включительно и т.д. Каждая такая группа называется разрядом оценок. В случае полного размещения по группам обычно говорят о распределении сгруппированных частот. Хотя и не существует четкого правила выбора количества разрядов, предпочтительнее образовывать не менее 12 и не более 15 разрядов. Иметь менее 12 разрядов рискованно из-за возможного искажения результатов, в то время как наличие более 15 разрядов затрудняет работу с таблицей.
Четвертый этап - построение распределения сгруппированных частот. Этот процесс построения обычного распределения сгруппированных частот складывается, в свою очередь, еще из четырех этапов. Они показаны в таблице 4, использующей оценки таблицы 2.
71
Таблица 3
Оценки диагностического исследования из таблицы 2, упорядоченные по величине, проранжированные и протабулированные
| Убывающая последовательность |
Ранг |
Табулирование без последующего группирования |
| Оценка |
Частота |
| 112 |
|
|
1 |
112 |
1 |
 |
Сумма = 19 |
| 109 |
|
|
2 |
109 |
1 |
| 106 |
|
|
3 |
106 |
1 |
| 105 |
|
|
4 |
105 |
1 |
| 104 |
|
|
5 |
104 |
1 |
| 100 |
|
|
6 |
100 |
1 |
| 97 |
 |
 |
7,5 |
97 |
2 |
| 97 |
7,5 |
95 |
2 |
| 95 |
 |
 |
9,5 |
93 |
1 |
| 95 |
19,5 |
91 |
1 |
| 93 |
|
|
11 |
90 |
1 |
| 91 |
|
|
12 |
89 |
1 |
| 90 |
|
|
13 |
84 |
2 |
| 89 |
|
|
14 |
83 |
1 |
| 84 |
 |
 |
15,5 |
82 |
1 |
| 84 |
15,5 |
81 |
1 |
| 83 |
|
|
17 |
|
|
|
Середина частот |
| 82 |
|
|
18 |
80 |
1 |
 |
Сумма = 19 |
| 81 |
|
|
19 |
78 |
1 |
| 80 |
|
|
20 |
75 |
3 |
| 78 |
|
|
21 |
74 |
1 |
| 75 |
 |
 |
23 |
72 |
1 |
| 75 |
23 |
71 |
1 |
| 75 |
23 |
70 |
1 |
| 74 |
|
|
25 |
69 |
1 |
| 72 |
|
|
26 |
68 |
1 |
| 71 |
|
|
27 |
66 |
1 |
| 70 |
|
|
28 |
62 |
1 |
| 69 |
|
|
29 |
59 |
2 |
| 68 |
|
|
30 |
58 |
1 |
| 66 |
|
|
31 |
51 |
1 |
| 62 |
|
|
32 |
47 |
1 |
| 59 |
 |
 |
33,5 |
44 |
1 |
| 59 |
33,5 |
|
|
|
|
| 58 |
|
|
35 |
|
n = 38 = 19 + 19 |
| 51 |
|
|
36 |
|
|
|
|
| 47 |
|
|
37 |
|
|
|
|
| 44 |
|
|
38 |
|
|
|
|
72
Таблица 4
Иллюстрация процесса построения и распределения сгруппированных частот
| Исходные оценки (из табл. 2) |
Этапы построения распределения |
90
66
106
84 |
Этап 1. Определение размаха
Самая высокая оценка112
Самая низкая оценка 44
Размах = Разность + 1 = 68 + 1 = 69 |
105
83
104
82
97
97
59
95
78
70 |
Этап 2. Выбор интервала разрядов
69 : 12 = 5,75 наибольший возможный разрядный интервал
Округляем с уменьшением до 5
69 : 15 = 4,60 наименьший возможный разрядный интервал
Округляем с увеличением до 5 |
| 47 |
Этапы 3 и 4. Определение границ разрядов и табулирование |
95
100 |
Внутренние численные границы 15 разрядов |
Подсчет |
Частота (t) |
69
44
80
75
75
51
109
89
58
59
72
74
75
81
71
68
112 |
110 - 114
105 - 109
100 - 104
95 - 99
90 - 94
85 - 89
80 - 84
75 - 79
70 - 74
65 - 69
60 - 64
55 - 59
50 - 54
45 - 49
40 - 44
|
1
111
11
1111
111
1
111111
1111
1111
111
1
111
1
1
1
|
1
3
2
4
3
1
6
4
4
3
1
3
1
1
1
|
62
91
93
84 |
|
|
n =38 |
73
1. Определение общего размаха внутри всей выборки, который равен разности между максимальной и минимальной оценками плюс единица. Из имеющихся оценок максимальная равна 112, минимальная - 44, что дает размах (112 - 44) + 1 = 69. Фактически считают, что 112 покрывается единичным интервалом оценок 112,5 - 111,5, а 44 - интервалом 44,5 - 43,5. Заметим далее, что размах равен 69 [(112 - 44) + 1, или 112,5 - 43,5]. Однако реальные границы оценок не всегда являются дробными. Если возраст исчисляется от последнего (самого недавнего) дня рождения, то лица, объявившие себя 44-летними (т.е. еще не 45-летними), находятся в интервале 44,00 - 44,99... (почти, но не совсем 45,00), середина которого 44,5. Если они называют возраст относительно ближайшего дня рождения, интервал составляет 43,5 - 44,5 со средним 44. Аналогично, если они представляют себя приближающимися к 44, то интервал равен 43,00 - 43,99... со средним 43,5. Между самым "юным" из "приближающихся к 44", который только что достиг возраста 43 лет, и самым "старым" представителем "44-го последнего дня рождения", которому почти 45, будет наблюдаться разница приблизительно в два года. Спрашивая просто о возрасте без точного определения системы счета, мы не в состоянии точно интерпретировать результаты.
2. Выбор интервала группирования разрядов, представляющего собой ширину разрядов, по которым должны быть классифицированы оценки, должен производиться таким образом, чтобы разрядов было не менее 12, но и не более 15. Для этого разделим диапазон на 12 и найдем наибольший возможный класс или интервал разряда оценок. Разделим диапазон на 15 и найдем наименьший возможный интервал разряда (см. табл. 4). Так как использовать любой нецелый интервал неудобно, то наибольшее число округляется с уменьшением до 5, а наименьшее - с увеличением до 5, хотя и интервал 6 обеспечил бы 12 разрядов для этих 38 оценок.
Интервал с шириной, определяемой нечетным числом, например 5, с целочисленным средним значением, если границы разряда дробные (оканчивающиеся на 0,5), обычно предпочитают интервалу с четной шириной, но дробными средними, когда границы разряда дробные. Середина разряда 110 - 114, содержащего пять оценок: 110, 111, 112, 113 и 114, равна 112 (т.е. 110 + [(114 - 110) : 2] = 110 + 2 = 112). Другой способ определения середины интервала состоит просто в усреднении зафиксированных границ интервала: (110 + 114) : 2 = 112. Если бы использовался разряд шириной 6 с границами оценок, например 108 - 113, то середина этой группы, определяющейся четным числом, составила бы 110,5, что могло бы привести в итоге к более сложному счету. Следовательно, интервал 5 предпочтительнее интервала 6, когда границы разряда дробные.
74
3. Определение границ разрядов. Разумеется, надо образовать достаточное количество разрядов для включения самой высокой и самой низкой оценок. Для этого начинайте табулирование всегда с величины, кратной разрядному интервалу. Если самый низкий разряд начать с 40, кратного 5, он включит самую низкую оценку 44. А если начать с 45, то он не включит 44. Следующий разряд будет начинаться с 45, затем с 50 и т.д. до тех пор, пока самая высокая оценка 112 не попадет в разряд 110 - 114.
4. Табулирование. Подсчет ведется для каждой оценки против разряда, в который она попадает. Для табулирования нет необходимости в упорядочении оценок, так как последнее может потребовать больше времени, чем само табулирование. В первоначальном алфавитном списке первая оценка 90. В столбце таблицы против разряда, начинающегося с 90, для регистрации оценки делается черточка. Следующая оценка - 66. Она попадает в разряд, который начинается с 65, так что черточка делается там. Аналогично результаты подсчета помещаются в столбце против соответствующего разряда для всех прочих оценок.
В итоговой таблице не приводятся этапы, в результате которых она была получена. В простейшей форме распределения частот есть только два столбца. В первом приводятся разряды, обычно расположенные в убывающем порядке сверху вниз, а второй содержит частоты - число оценок в каждом разряде.
Когда нужно сравнить две или более выборок, обычно хорошо поместить все данные в такую же таблицу. В этом случае будет один столбец для разрядов, в который сгруппированы оценки, и по одному для каждой из сравниваемых, скажем школ или классов. В таблице 5 приведены распределения частот, обобщающие отчеты шести школ. Количество интервалов группирования меняется от 9 для школы Е до 17 для школ А и Г, хотя для некоторых интервалов нет данных.
Графическое представление распределения частот. Обычное распределение частот не дает вполне ясной картины. Существуют три общих метода графического представления распределения оценок: гистограмма, или столбиковая диаграмма, полигон распределения и сглаженная кривая.
Гистограмма - это последовательность столбцов, каждый из которых опирается на один разрядный интервал, а высота его отражает число случаев, или частоту, в этом разряде.
На рисунке 1 показана гистограмма, или столбиковая диаграмма, представляющая распределение 83 учащихся по коэффициенту интеллекта IQ (диаграмма отражает распределение показателей 16 учащихся, имеющих наибольший коэффициент IQ).
Полигон распределения. Построение полигона распределения во многом напоминает построение гистограммы. В гистограмме каждый столбец заканчивается горизонтальной линией, причем на
75
Таблица 5
Результаты тестирования знаний учащихся по математике для всех шести школ в одном городе
| Оценки |
А |
Б |
В |
Г |
Д |
Е |
Все шесть школ |
| 120 - 124 |
|
|
|
1 |
|
|
1 |
| 115 - 119 |
|
|
|
|
|
|
|
| 110 - 114 |
|
|
1 |
|
|
|
1 |
| 105 - 109 |
|
|
3 |
|
2 |
2 |
7 |
| 100 - 104 |
|
3 |
2 |
2 |
5 |
3 |
15 |
| 95 - 99 |
|
6 |
4 |
4 |
4 |
5 |
23 |
| 90 - 94 |
5 |
2 |
3 |
5 |
6 |
10 |
31 |
| 85 - 89 |
4 |
4 |
1 |
4 |
4 |
1 |
18 |
| 80 - 84 |
2 |
3 |
6 |
6 |
4 |
8 |
29 |
| 75 - 79 |
10 |
5 |
4 |
4 |
1 |
2 |
26 |
| 70 - 74 |
6 |
2 |
4 |
7 |
6 |
4 |
29 |
| 65 - 69 |
9 |
4 |
3 |
|
4 |
1 |
21 |
| 60 - 64 |
4 |
5 |
1 |
2 |
1 |
|
13 |
| 55 - 59 |
1 |
|
3 |
|
1 |
|
5 |
| 50 - 54 |
1 |
|
1 |
|
|
|
2 |
| 45 - 49 |
1 |
|
1 |
|
|
|
2 |
| 40 - 44 |
|
|
1 |
2 |
2 |
|
5 |
| 35 - 39 |
|
1 |
1 |
|
|
|
2 |
| 30 - 34 |
|
2 |
|
|
|
|
2 |
| 25 - 29 |
|
1 |
|
|
|
|
1 |
| 20 - 24 |
|
|
|
|
|
|
|
| 15 - 19 |
|
|
|
|
|
|
|
| 10 - 14 |
1 |
|
|
|
|
|
1 |
| N (число учащихся) |
44 |
38 |
39 |
37 |
40 |
36 |
234 |
высоте, соответствующей частоте в этом разряде. А в полигоне он заканчивается точкой над серединой своего разрядного интервала на той же высоте. Далее точки соединяются отрезками прямых (рис. 2).
Сглаженная кривая. Иногда вместо гистограммы или полигона строят сглаженную кривую. Единственная разница состоит в том, что сглаженная линия проводится по точкам настолько близко, насколько это возможно, а для других двух фигур используются линии с острыми углами или зубцами (рис. 3).
Как правило, особенно для малых групп, где чаще всего встречаются неравномерности, лучше пропустить некоторые точки, чтобы получить плавную и правильную кривую; но следует позаботиться о том, чтобы оставить приблизительно одинаковое количество точек по обе стороны кривой. Тогда линия будет как можно лучше сглаживать отклонения точек.
76

Рис. 1. Гистограмма, или столбиковая диаграмма, представляющая распределение 83 IQ учащихся небольшого колледжа
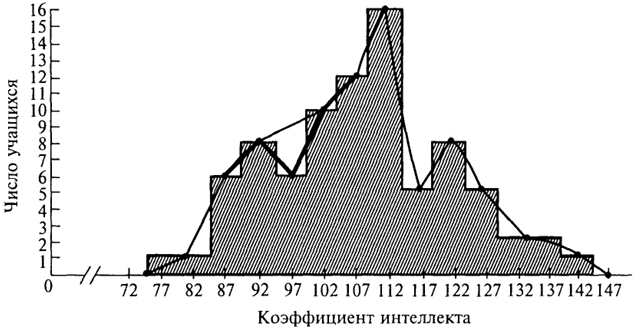
Рис. 2. Полигон распределения (ломаная линия) коэффициента интеллекта 83 учащихся колледжа
Нет сомнений в том, что графическое представление педагогических данных является ценным дополнением к статистическому анализу и обобщению. График или диаграмма имеет целью привлечь внимание читателя, потому что этот способ показывает процесс в динамике. Один маленький график порой больше проясняет суть дела, чем дюжина таблиц или написанных параграфов. Действительно, статистики часто немы, таблицы нередко молчаливы, и только график громко заявляет о своей миссии. Обычно количественные данные совершенно абстрактны. Рисунок или график дает более конкретное представление о существе вопроса.
77
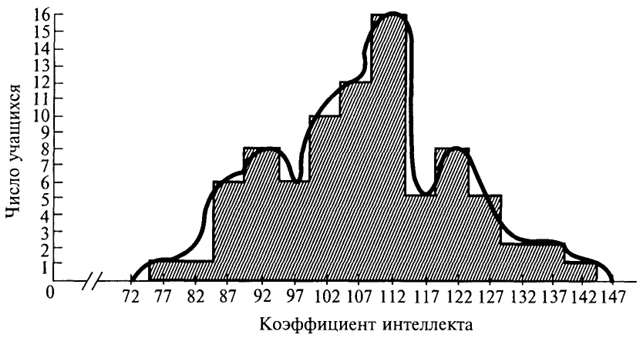
Рис. 3. Сглаженная кривая полигона распределения коэффициента интеллекта 83 учащихся колледжа
- Какие измерительные шкалы могут применяться в педагогической диагностике?
- Расскажите, как осуществляется процесс табулирования полученных диагностических данных.
- В каком виде нужно представить количественные данные как конечный результат диагностических исследований?
78
