§ 6. Перемена плоскостей проекций

Пусть дана система двух взаимно перпендикулярных плоскостей проекций V и H. В дальнейшем такую систему будем обозначать X

V

H

 .

Проекциями произвольно расположенной в пространстве точки А на эти плоскости будут а и а' (рис. 17, а).

Проследим, как изменяются проекции точки А, если плоскость V заменить новой плоскостью проекции V₁. Плоскость V₁ проводится перпендикулярно Н.

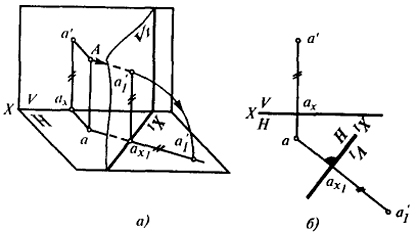
Рис. 17

21

Положение горизонтальной плоскости проекции Н остается без изменения. Плоскости V₁ и H пересекаются по прямой X₁, определяющей новую ось проекции; а'₁ - новая фронтальная проекция точки А на V₁.

Горизонтальная проекция точки А не изменит своего положения, так как при замене V плоскостью V₁ взаимное расположение точки А и плоскости Н не менялось, не менялось также и направление проектирования на Н.

Следовательно, при переходе от системы плоскостей проекции X

V

H

 к новой системе X₁

V1

H

получим вместо проекций а и а' новые проекции а и а'₁.

Легко убедиться, что расстояние новой фронтальной проекции а'₁ точки А от новой оси Х₁ равно расстоянию старой фронтальной проекции а' от старой оси X, т.е. а'а_х = а'₁а_х1.

Чтобы перейти от пространственного макета к эпюру, нужно совместить плоскость V₁ с плоскостью чертежа.

Способ перемены плоскостей проекций предусматривает совмещение новой плоскости проекции с той из старых плоскостей, по отношению к которой она была перпендикулярна. В нашем случае (ввиду перпендикулярности V₁ и Н) плоскость V₁ совмещается с Н. За ось вращения принимается новая ось проекций (представляющая след плоскости V₁ на Н). Направление поворота не оказывает никакого влияния на ответ задачи. Поворот следует делать так, чтобы новые проекции не накладывались на старые. На рис. 17, а совмещение плоскости V₁ с Н осуществлено вращением ее по направлению движения часовой стрелки.

Равенство аппликат у новой а'₁ и старой а' фронтальной проекций точки А и использование в обоих случаях прямоугольного проецирования делает построения новой фронтальной проекции чрезвычайно простыми (рис. 17, б)¹. Они состоят в том, что через старую горизонтальную проекцию точки проводят перпендикуляр к новой оси и откладывают на нем от точки пересечения с осью величину, равную расстоянию старой фронтальной проекции от старой оси (см. рис. 17, б).

22

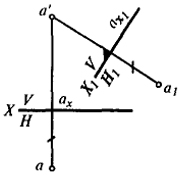
Рис. 18

Замена горизонтальной плоскости Н новой плоскостью Н₁ и построение новых проекций точки А в системе X₁

V

H1

 осуществляется аналогично только что рассмотренному случаю, с той лишь разницей, что теперь остается без изменения фронтальная проекция точки, а для нахождения новой горизонтальной проекции а₁ точки А необходимо из старой фронтальной проекции точки опустить перпендикуляр на новую ось и отложить на нем от точки пересечения с осью величину, равную расстоянию старой горизонтальной проекции от старой оси.

Построения, выполненные по этому правилу, приведены на рис. 18.

Зная правила построения новой проекции одной точки, можно построить новые проекции любого числа точек, а следовательно, и любой линии и фигуры.

Точку, через которую проводится ось, и направление оси можно выбирать произвольно. Следует следить лишь за тем, чтобы не происходило накладывания новых проекций на старые и чтобы геометрические элементы, расположенные в первой четверти пространства, оставались в ней и после перемены плоскости проекции.

Часто при определении натуральной величины какого-либо предмета или для получения более наглядного его изображения необходимо переменить не одну, а две плоскости проекций.

Следует иметь в виду, что нельзя менять обе плоскости сразу. Перемена двух плоскостей проекции может осуществляться только последовательно - вначале меняют одну плоскость, затем - другую, т.е. если нам надо перейти от заданной системы плоскостей X

V

H

 к новой Х₂

V1

H1

, то такой переход может быть осуществлен по одной из приведенных ниже схем:

Х

V

H

 → Х₁

V1

H

 → Х₂

V1

H1

или

Х

V

H

 → Х₁

V

H1

 → Х₂

V1

H1

23

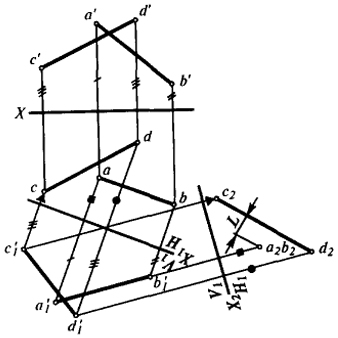
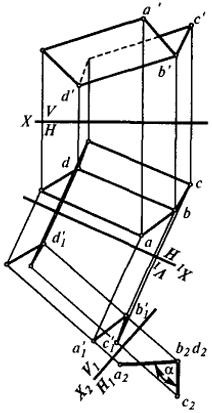
Рис. 19	Рис. 20

Рассмотрим на примерах, как задаются новые плоскости и способы определения новых проекций при замене двух плоскостей проекций.

Задача 1. Определить расстояние между скрещивающимися прямыми АВ и CD (рис. 19).

Меняем плоскости проекции так, чтобы одна из прямых, например аb, а'b', оказалась перпендикулярной к новой плоскости проекции. Так как прямая аb, а'b' общего положения, то следует произвести две последовательные замены плоскостей: после первой замены прямая аb, а'b' должна оказаться параллельной фронтальной (горизонтальной) плоскости проекции; в результате второй замены эта прямая должна стать перпендикулярной к новой горизонтальной (фронтальной) плоскости.

На рис. 19 вначале проведена ось Х₁ параллельно ab и найдены новые фронтальные проекции а'₁b'₁ и c'₁d'₁. Затем проводится ось X₂ перпендикулярно a'₁b'₁.

Величина L - расстояние между новыми горизонтальными проекциями прямых а₂b₂ и c₂d₂ определяет искомое расстояние между прямыми АВ и CD.

Задача 2. Определить угол между плоскостями Q (DB × АВ) и S(DB × CB) (рис. 20).

24

Задача решается аналогично предыдущей. Путем замены плоскости V на V₁, а Н на Н₁ переходим от системы Х

V

H

 к новой системе Х₂

V1

H1

, в которой линия пересечения плоскостей BD будет перпендикулярной плоскости H₁. Такое положение прямой BD предрешает перпендикулярность плоскостей Q и S новой горизонтальной плоскости. Поэтому угол а₂b₂c₂, равный α, будет искомым.

25