Совмещение является частным случаем вращения плоскости вокруг горизонтали и фронтали.
При совмещении за ось вращения принимается не произвольная горизонталь или. фронталь плоскости, а ее горизонтальный или фронтальный след2 .
18
 |
 |
| Рис. 13 |
Рис. 14 |
В таком случае, в результате поворота плоскости, она совместится либо с плоскостью Н, если вращение осуществляется вокруг горизонтального следа плоскости, либо с V при вращении вокруг фронтального следа.
Совмещение, так же, как и вращение вокруг горизонтали или фронтали, применяется в тех случаях, когда требуется определить истинный вид фигур, лежащих в плоскости, или построить в плоскости общего положения фигуру, форма и размеры которой заданы.
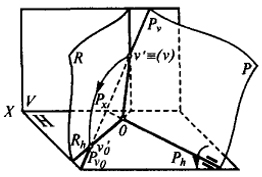
Сущность способа совмещения можно уяснить из следующих рассуждений. Плоскость общего положения Р (рис. 13) вращаем вокруг следа Ph до совпадения ее с горизонтальной плоскостью проекции. Тогда все точки, лежащие в плоскости Р, совместятся с плоскостью Н. При этом преобразовании след Рh, как ось вращения, останется на месте. Поэтому для нахождения совмещенного положения плоскости достаточно найти совмещенное положение только одной принадлежащей ей точки. В качестве такой точки целесообразно взять любую точку v', лежащую на фронтальном следе плоскости. Точкаv' при вращении вокруг оси Ph будет перемещаться по дуге окружности, лежащей в плоскости R, перпендикулярной к оси вращения.
Построения, которые нужно сделать, чтобы определить совмещенное положение точки v' с плоскостью Н при вращении ее вокруг следа Ph, аналогичны построениям для нахождения положения точки В0 (см. рис. 11).
Соединяем совмещенное положение точки v'0 с точкой схода следов Рх, которая, как лежащая на оси вращения, при данном преобразовании не изменит своего положения, получим совмещенное с H положение фронтального следа плоскости Рv0. На рис. 14, а все построения приведены на эпюре.
19
 |
 |
| Рис 15 |
Рис 16 |
Так как на плоскость H все элементы плоскости Р проектируются в натуральную величину, то, очевидно, расстояние от точки схода следов Рх до v' на фронтальном следе будет равно расстоянию от Рх до v'0, на совмещенном положении следа Pv0.
Поэтому положение точки V', а следовательно, и следа Pv0 можно определить, не пользуясь центром и радиусом вращения.
Для этого достаточно из точки Рх описать дугу радиусом, равным расстоянию Pxv' до ее пересечения с горизонтальным следом плоскости, в которой будет перемещаться точка v'. Через полученную точку и пройдет фронтальный след плоскости Рv0 при совмещении его с плоскостью H (рис. 14, б).
Рис. 14, б показывает совмещение плоскости Р с плоскостью проекций H.
Проследим на конкретных примерах использование способа совмещения для решения задач.
Задача 1. Определить натуральную величину трапеции ABCD, лежащей в плоскости Р (рис. 15). Решить вращением вокруг фронтального следа.
Находим совмещенное с плоскостью V положение горизонтального следа Рh0 . Через a'b'c'd' проводим фронтальные проекции горизонталей, а через точки v'1, v'2, v'3, v'4 - их совмещенное направление. Совмещенное положение вершин трапеции A0B0C0D0 определится пересечением этих горизонталей с перпендикулярами к Pv, восставленными
20
из фронтальных проекций вершин трапеции. A0B0C0D0 является искомой натуральной величиной трапеции.
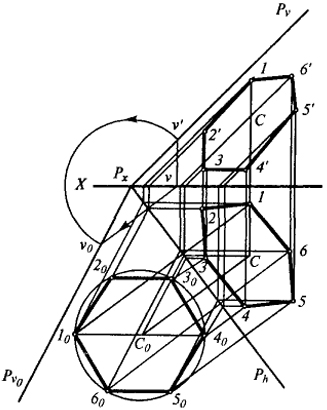
Задача 2. На плоскости Р построить правильный шестиугольник, если известна величина радиуса описанной окружности и положение ее центра С (рис. 16).
Для решения задачи совместим плоскость Р с H. Из точки С0 описываем окружность радиусом заданной величины и строим правильный шестиугольник 10, 20, З0, 40, 50, 60. Теперь необходимо повернуть плоскость Р из совмещенного положения в исходное (поднять в пространство). Вместе с плоскостью Р повернутся и все точки, лежащие в ней, в том числе и вершины шестиугольника.
Затем через вершины шестиугольника 10, 20, З0, 40, 50, 60 проводим совмещенные фронтали и прямые, перпендикулярные следу Ph. Находим точки h1, h2, h3, h4, h5, h6 (на рис. 16 эти точки не показаны), через них пройдут горизонтальные проекции фронталей, пересечение которых с перпендикулярами определяет горизонтальные проекции вершин шестиугольника 1, 2, 3, 4, 5, 6. По горизонтальным проекциям находим фронтальные проекции 1', 2', 3', 4', 5', 6'.
21
2
Совмещение можно осуществить и с плоскостью W путем вращения плоскости вокруг ее профильного следа. При этом характер графических построений ничем не будет отличаться от построений, рассмотренных ниже.
