§ 4. Вращение вокруг горизонтали
или фронтали

При решении метрических задач для упрощения решения оказывается целесообразным переместить плоскость, в которой расположены рассматриваемые фигуры, в положение, параллельное какой-либо плоскости проекций.

Такое перемещение может быть осуществлено путем вращения плоскости вокруг оси, параллельной плоскости проекций.

Очевидно, вращая плоскость вокруг горизонтали, можно привести ее в положение, параллельное плоскости проекции H, это, в свою очередь, даст возможность спроецировать на H без искажения все находящиеся в этой плоскости геометрические элементы.

Вращением плоскости вокруг фронтали можно перевести ее в положение, параллельное фронтальной плоскости проекции V, это обеспечит получение на фронтальной плоскости проекции натуральной величины всех принадлежащих плоскости геометрических элементов.

Так как при данном преобразовании осями вращения являются горизонталь или фронталь, оно называется вращением вокруг горизонтали или фронтали.

16

Каждая точка плоскости при ее вращении будет перемещаться по окружности, расположенной в плоскости, перпендикулярной оси вращения. Центр окружности будет находиться на оси вращения, а величина радиуса вращения равна расстоянию от точки до оси.

Если за ось вращения взята горизонталь, то окружность (представляющая траекторию движения точки) будет проецироваться на плоскость Н в отрезок прямой, перпендикулярной горизонтальной проекции горизонтали.

Точка пересечения горизонтальных проекций горизонтали и окружности определяет горизонтальную проекцию центра вращения. На плоскость V окружность спроецируется в эллипс, построение которого можно не делать.

Аналогично, при вращении плоскости вокруг фронтали любая точка плоскости перемещается по окружности, которая будет проецироваться на плоскость V в отрезок прямой, перпендикулярный фронтальной проекции фронтали; на плоскость H в эллипс, в вычерчивании которого также нет необходимости.

Проследим на конкретном примере, как осуществляется поворот плоскости вокруг горизонтали в положение, параллельное плоскости проекции Н.

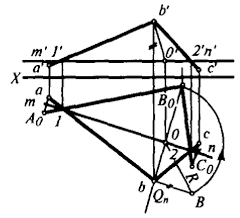
Пример 1. Плоскость Р, заданную двумя пересекающимися прямыми АВ и ВС, повернуть вокруг горизонтали так, чтобы она стала параллельной плоскости Н (рис. 11).

В плоскости Р проводим горизонталь MN, которая пересекает прямые, определяющие плоскость в частных точках 1,1' и 2,2'. При вращении плоскости вокруг оси MN две ее точки 1,1' и 2,2', как принадлежащие оси вращения, не изменяет своего положения и после поворота плоскости. Поэтому для определения нового (параллельного плоскости Н) положения плоскости достаточно повернуть только одну точку, принадлежащую плоскости и не лежащую на прямой MN.

Для упрощения дальнейших построений возьмем точку В и повернем ее вокруг MN так, чтобы после поворота ее новое положение В₀ совместно с точками 1 и 2 определяло новое положение плоскости Р, параллельное плоскости проекции H.

Чтобы повернуть точку, необходимо найти положение центра вращения и определить величину радиуса вращения.

Центр вращения точки В (рис. 11) находится в точке пересечения оси вращения с плоскостью Q, определяемой окружностью, по которой перемещается точка (плоскость Q перпендикулярна MN). Найдя проекции центра вращения (оо'), легко определить величину радиуса вращения оВ.

17

Рис. 11	Рис. 12

Далее из точки о радиусом оВ проводим дугу до пересечения ее с прямой оb - горизонтальной проекцией окружности, по которой перемещается точка В¹ Пересечение даст нам искомую точку В₀.

Соединив точку В₀ с точками 1 и 2, получим новое направление прямых ВА и ВС, параллельных плоскости Н.

Если по условиям задачи необходимо найти положение точек А₀ и С₀, то достаточно из а и с провести перпендикуляры к тп до пересечения их с В₀1 и В₀2.

Вращение вокруг фронтали осуществляется аналогично рассмотренному примеру. На рис. 12 плоскость р (АВ × ВС) повернута около фронтали KL до положения, параллельного фронтальной плоскости проекции.

Построения проведены в той же последовательности, что и на рис. 11.

18