Способ вращения вокруг осей, перпендикулярных плоскостям проекций, обладает тем недостатком, что новые проекции накладываются на первоначальные, вследствие чего эпюр теряет наглядность. Этому способствует также нанесение на эпюре дуг окружностей, представляющих проекции траекторий перемещения точек.
Вращение точки вокруг осей, перпендикулярных плоскостям проекций, можно рассматривать как частный случай более общего вида перемещения параллельно плоскостям проекций. Следовательно, не только при движении по окружности (вращение), но и при всяком перемещении точки в плоскости, параллельной Н, ее фронтальная проекция передвигается по прямой, параллельной оси X.
В случае произвольного перемещения точки в плоскости, параллельной V, ее горизонтальная проекция передвигается по прямой, параллельной оси X.
Справедливость отмеченных свойств может быть легко показана на простом примере.
Представим плоскость Т, параллельную горизонтальной плоскости проекций Н. Пусть точка А, лежащая в этой плоскости, переместится из положения А в положение А1, двигаясь в плоскости по произвольной траектории (рис. 8, а).
Очевидно, фронтальная проекция точки А переместится при этом из а' в а'1 и будет лежать на фронтальном следе Tv.
На рис. 8, б показано перемещение точки В, принадлежащей плоскости S, которая параллельна фронтальной плоскости V. Горизонтальная

Рис. 8
14
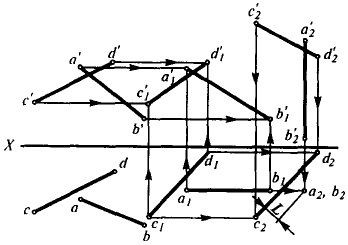
Рис. 9
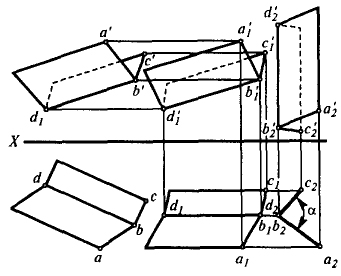
Рис. 10
проекция точки В будет перемещаться по горизонтальному следу Sh. Из чертежа следует, что перемещение горизонтальной проекции точки В, так же, как и фронтальной проекции точки А, не зависит от характера перемещения точки в плоскости.
Используя эти свойства, можно в ряде случаев упростить геометрические построения, приведенные в предыдущем параграфе и, главное, сделать их более наглядными. Последнее достигается тем, что мы не привязываем новые проекции к определенным осям вращения, а перемещаем их так, чтобы избежать наложения одной проекции на другую.
Рассмотрим на примерах решения задач использование способа параллельного перемещения.
Задача 1. Определить расстояние между скрещивающимися прямыми АВ и CD (рис. 9).
Перемещаем прямые АВ и CD так, чтобы одна из прямых, например АВ, заняла положение, перпендикулярное горизонтальной плоскости
15
проекции. Так как прямая АВ общего положения, следует произвести два последовательных перемещения: одно - параллельно горизонтальной плоскости проекции, другое - параллельно фронтальной плоскости проекции.
Расстояние между прямыми АВ и CD определяется величиной L - удаления горизонтальной проекции a2b2 от c2d2.
Задача 2. Определить угол между плоскостями Q (BD × АВ) и S (BD × CB) (рис. 10).
В предыдущем параграфе (см. рис. 7) эта задача была решена вращением плоскостей вокруг осей, перпендикулярных V и H, до тех пор, пока они не займут положения, перпендикулярного плоскости Н. Осуществим теперь такой переход, использовав для этого параллельное перемещение.
На рис. 10 плоскости Q и S перемещаются вначале параллельно плоскости Н, затем параллельно плоскости V, в результате этих двух перемещений линии пересечения плоскостей BD и сами плоскости займут положение, перпендикулярное H, угол a2b2c2 равен искомому углу α.
16
