Проследим, как будет изменяться положение проекций точки А при ее вращении вокруг оси J, перпендикулярной фронтальности плоскости проекции V.
При вращении вокруг оси J (рис. 4, а) точка А будет перемещаться в плоскости S, перпендикулярной оси вращения (а следовательно, параллельной плоскости V). Траекторией движения точки будет окружность с центром на оси вращения и радиусом, равным расстоянию от точки до этой оси.
Ввиду того что окружность, по которой перемещается точка, лежит к плоскости S, параллельной плоскости V, траектория движения точки будет проецироваться на плоскость V в виде окружности того же радиуса R, на плоскость H - в виде прямой, параллельной оси Х.
Если переместить точку из положения Ав положение А1 путем поворота на некоторый угол α, то фронтальная проекция из а' перейдет в положение а'1, описав при этом дугу а'a'1, опирающуюся на тот же угол α. Горизонтальная проекция а переместится по прямой аа1.
На рис. 4, б показано (на эпюре) изменение положения проекций точки А при ее повороте вокруг оси J на угол α.
Таким образом, при вращении точки вокруг оси, перпендикулярной фронтальной плоскости проекций, фронтальная проекция точки перемещается
11
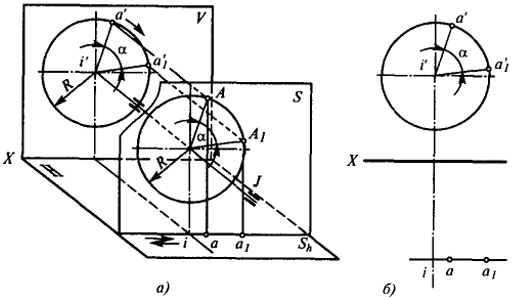
Рис. 4
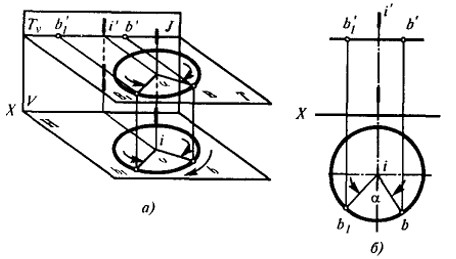
Рис. 5
по окружности с центром на фронтальной проекции оси вращения, а горизонтальная - по прямой, параллельной оси X.
Вращение точки вокруг оси J, перпендикулярной горизонтальной плоскости проекции Н, показано на рис. 5, а и б.
Точка В перемещается по окружности, лежащей в плоскости Т, перпендикулярной оси вращения.
Так как ось вращения перпендикулярна плоскости Н, то плоскость Т окажется параллельной плоскости Н; поэтому траектория перемещения точки В будет проецироваться на плоскость Н без искажения, а на плоскость V - в виде отрезка прямой.
Таким образом, при вращении точки вокруг оси, перпендикулярной горизонтальной плоскости проекции, горизонтальная проекция точки перемещается по окружности с центром на горизонтальной проекции оси вращения, а фронтальная - по прямой, параллельной оси X.
12
 |
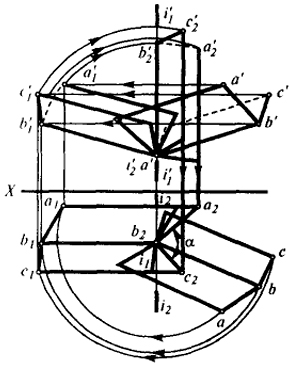 |
| Рис. 7 |
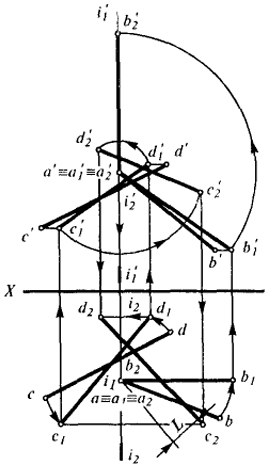
Рис. 6 |
Зная правила, которым подчиняются перемещения проекций точки при ее вращении в пространстве, нетрудно выполнить на эпюре поворот фигуры.
Задача 1. Определить расстояние между скрещивающимися прямыми АВ и CD (рис. 6).
Для определения расстояния между скрещивающимися прямыми непосредственно по эпюру необходимо привести его к такому виду, чтобы одна из прямых проецировалась в точку. Это будет соответствовать переводу плоскостей параллелизма, в которые мы мысленно заключаем заданные прямые, в положение проецирующих плоскостей. Все построения, связанные с получением такой проекции, показаны на рис. 6.
Вращение прямых АВ и CD осуществляем последовательно вокруг двух осей J1 ⊥ H и J2 ⊥ V, в обоих случаях ось проходит через точку А. Построения видны из чертежа и не нуждаются в пояснениях.
Искомое расстояние равно величине L - удаления горизонтальной проекции a2b2 от c2d2.
Задача 2. Определить угол между плоскостями Q(BD × АВ) и S (BD × СВ). Угол между плоскостями спроецируется на плоскость проекции в натуральную величину, если плоскости Q и S будут перпендикулярны этой плоскости (рис. 7).
13
Поэтому задача сводится к преобразованию заданных плоскостей в положение проецирующих.
Для осуществления такого преобразования нужно, чтобы линия их пересечения была перпендикулярна плоскости проекции.
Прямая BD последовательным вращением вокруг осей J1 и J2 переведена в положение горизонтально-проектирующей прямой.
Все построения ясны из чертежа на рис. 7.
14
