Способ квадратичных преобразований для определения линии пересечения поверхностей можно использовать только в сочетании с обычным способом решения с помощью секущих плоскостей.
Задача решается в следующей последовательности:
- 1) заданные поверхности рассекают плоскостью;
- 2) квадратичным преобразованием кривые, полученные в результате сечения поверхностей плоскостью, превращают в прямые линии;
- 3) находят точки пересечения этих прямых; полученные точки будут искомыми в преобразованном положении;
- 4) обратными построениями определяют их ортогональные проекции.
138

Рис. 128
Для получения достаточного количества точек, необходимых для построения кривой линии пересечения, эти операции повторяются несколько раз.
Преимущество данного способа решения задачи состоит в том, что не нужно строить лекальные кривые, это значительно упрощает решение, достигается более высокая точность ответа.
К сожалению, область применения этого способа ограничена. Он может быть использован только в тех случаях, когда поверхности будут расположены так, что кривые, полученные при сечении вспомогательными плоскостями, будут иметь общую ось и фокус.
Примером такого расположения поверхностей является случай, разобранный в задаче, приведенной ниже.
Задача. Определить линию пересечения эллиптического параболоида с цилиндром, ось которого - кривая, проходящая через фокусы эллипсов сечения параболоида (рис. 128).
139
Эллиптический параболоид и цилиндр рассекают рядом плоскостей Q, параллельных горизонтальной плоскости проекции. Эти плоскости пересекут параболоид по эллипсам, цилиндр - по окружностям, центры которых совпадут с одним из фокусов эллипса. Затем эти эллипсы и окружности преобразуют в прямые и находят точки их пересечения, которые прямым квадратичным преобразованием превращают в две соответствующие точки.
На рис. 128 указанные построения выполнены для сечения плоскостью Q2.
Половина большой оси эллипса сечения равна o'2a'2 для определения величины малой оси на чертеже проведена кривая d'1d'2s'2, представляющая собой совмещенную с плоскостью V профильную проекцию половины очерка параболоида. Отрезок d'2o'2 равен малой полуоси эллипса.
От горизонтальной проекции точки о2 на направлении малой оси эллипса откладывают отрезок od2, равный o'2d'2.
Для нахождения фокуса эллипса, с которым совпадает центр преобразования, из точки d2 (горизонтальной проекции одного из концов малой оси эллипса) проводят дугу окружности радиусом, равным величине большой полуоси эллипса о'2а'2. Пересечение этой дуги с большой осью эллипса определит положение точки f2 - горизонтальной проекции одного из фокусов эллипса. Через f2 проводят проекции двойной прямой p2 и граничных прямых MN и KL.
Перпендикуляры, восстановленные из точек а2 и b2 к большой оси эллипса, пересекут граничную прямую KL в точках a и b, определяющих прямую, в которую преобразуется эллипс. Окружность преобразуется в прямую et1.
Прямые ab и et пересекаются в точке II. Преобразовывая ее, получают точки 21 и 32; по ним определяют фронтальные проекции 21 и 32. С помощью секущих плоскостей Q1 и Q3 находят точки 111'1, 121'2, 313'1, 323'2 (на чертеже построения не указаны). Соединив их плавной кривой, находят искомую линию пересечения.
Способ квадратичных преобразований возможно применить также в тех случаях, когда одна из пересекающихся поверхностей торовая.
Если расположить торовую поверхность так, чтобы ее ось оказалась перпендикулярной плоскости H, то при сечении этой поверхности
140
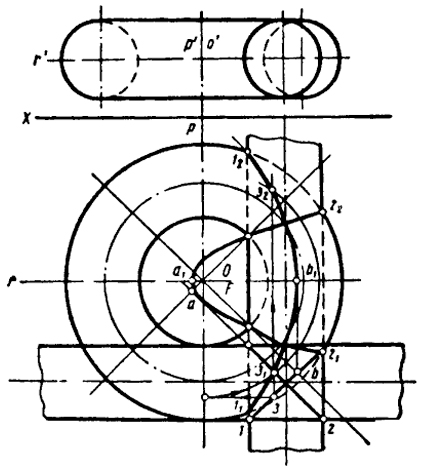
Рис. 129
горизонтальными плоскостями в сечении будут окружности, которые преобразуются в прямые, параллельные оси X (см. рис. 123). Следовательно, торовая поверхность может быть преобразована в цилиндрическую.
Допустим, требуется определить линию пересечения тора с цилиндром (рис. 129).
Принимаем за центр квадратичного преобразования точку О пересечения осей тора; за двойную линию р - ось симметрии тора, перпендикулярную плоскости V.
Ось симметрии преобразования r будет параллельна оси X.
При таком задании преобразования тор преобразуется в прямой круговой цилиндр с осью, параллельной оси X, а цилиндр преобразуется сам в себя.
Линией пересечения двух цилиндров равного диаметра с пересекающимися осями будут, как известно, эллипсы, если оси цилиндров пересекаются под произвольным углом, или окружности, если оси перпендикулярны. При этом, если оси цилиндров параллельны какой-либо плоскости проекций, то на эту плоскость эллипсы (окружности) спроецируются в отрезки прямых. В данном случае горизонтальные проекции линий пересечения двух цилиндров будут прямые, соединяющие точки пересечения крайних образующих цилиндров.
141

Рис. 130
Из рис. 129 видно, что проекции 121 и 231 параллельны граничным прямым. Такие прямые, как уже известно (рис. 124), при квадратичном преобразовании превращаются в параболы. Фокусы парабол должны совпадать с центром преобразования О. Вершины парабол А1 и В1 легко найти с помощью точек А и В, в которых прямые 121 и 231 пересекаются с граничными прямыми. Положение фокуса и вершина вполне определяют параболу.
На рис. 129 показано построение точек 31 и З2 параболы, в которую преобразуется точка 3 прямой 121.
В 1965 г. была опубликована статья Нгуен Ван Дьема "К вопросу исследования квадратичного преобразования" [22], в которой автор излагает новый (отличный от предложенного О.В. Локтевым) способ задания квадратичного преобразования. Сущность этого способа состоит в следующем.
Пусть точка О - начало прямоугольной системы координат плоскости Q (рис. 130). Проведем прямые l1 и l2, параллельные оси х и отстоящие от нее на расстоянии, равном е. Назовем прямые l1 и l2 граничными прямыми, а величину е - коэффициентом преобразования.
Возьмем в плоскости Q точку А, ордината которой больше величины коэффициента преобразования (у(·)А > е).
Проведем через точку А прямую q, перпендикулярную оси х. Будем считать, что каждая точка плоского поля, инцидентная прямой q, преобразуется в две точки, также инцидентные q.
Для нахождения этих точек выполним следующие построения. Из точки Ах проведем дугу окружности радиусом, равным АxА, отметим точку ее пересечения с прямой l1 (или l2) A0 и из полученной точки опустим перпендикуляр АА'0 на ось х. Через точку A0 из центра Ах проводим дугу радиусом АxА'0.
Точки A1 и A2, в которых эта дуга пересекает прямую q, будут соответствовать данной точке А (при заданном квадратичном преобразовании, определяемом положением центра О и величиной е).
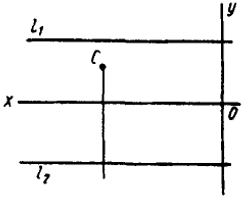
Если ордината точки В равна величине коэффициента преобразования (у(·)B = е), точка В инцидентна прямой l1 (или l2), то, как это видно из чертежа (рис. 131), она преобразуется в две действительные совпадающие точки, инцидентные оси xo.
Точка С, ордината которой меньше величины коэффициента преобразования (у(·)c < е), преобразуется в мнимые точки (рис. 132).
142
 |
 |
| Рис. 131 |
Рис. 132 |
 |
 |
| Рис. 133 |
Рис. 134 |
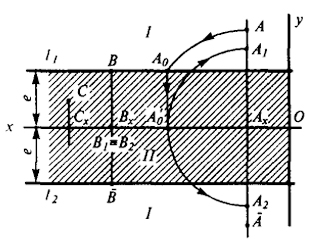
Приведенные чертежи показывают, что данное квадратичное преобразование, как и рассмотренное выше преобразование по схеме О.В. Локтева, позволяет преобразовать точку в зависимости от ее положения на плоскости (при заданном положении начала координат и величине коэффициента преобразования) в две действительные различные точки (рис. 130), две действительные совпадающие точки (рис. 131) и мнимые точки (рис. 132). На рис. 133 показаны две области I к II (аналогичные областям I и II, рис. 120).
Любая точка области I преобразуется в две действительные несовпадающие точки; любая точка области II преобразуется в мнимые точки. Точки, лежащие на границе этих областей, преобразуются в две действительные совпадающие точки.
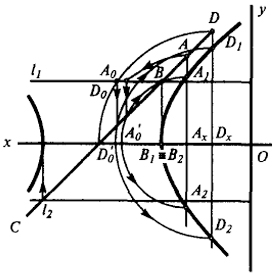
Если взять прямую общего положения, то она преобразуется в гиперболу, симметричную оси x (рис. 134).
Действительно, значение ординаты точки А1 (рис. 133):
y21= (A1Ax)2= (A0Ax)2= (AAx)2- (A0A'0)2=y2- e2;
y1 = ±√y2 - e2
143
следовательно, координаты точек А1 и А2 равны
| x1(2) = x; |
} |
| y1(2) = ±√y2-e2 |
(1)
или
| x = x1(2); |
} |
| y = ±√y1(2)2-e2 |
(2)
Теперь рассмотрим случай, изображенный на рис. 134.
Уравнение прямой CD
y = kx + b
после преобразования по формулам (2) примет вид:
Формула (3) есть уравнение гиперболы, симметричной относительно оси х. Следует иметь в виду, что преобразуемая прямая является асимптотой гиперболы.
В частном случае прямая, параллельная оси х, преобразуется в прямую (точнее, в две прямых), параллельных оси х; прямая, перпендикулярная оси х, преобразуется сама в себя.
Следуя аналогичным путем, не составляет труда показать, что любая кривая второго порядка, если одна из осей совпадает с осью симметрии преобразования (осью x), преобразуется в новую кривую второго порядка, гомотетичную исходной кривой с центром гомотетии, совпадающим с центром кривой (строго говоря, преобразуется не вся кривая, а лишь ее часть, расположенная в зоне действительных преобразований).
Рассмотренные преобразования по сравнению с преобразованиями О.В. Локтева являются более гибкими, так как мы можем выбирать произвольное расстояние граничной прямой l от оси х, что предопределяет разное значение коэффициента преобразования.
Преобразования Нгуен Ван Дьема позволяют упростить решение некоторых задач по определению линии пересечения двух поверхностей.
144
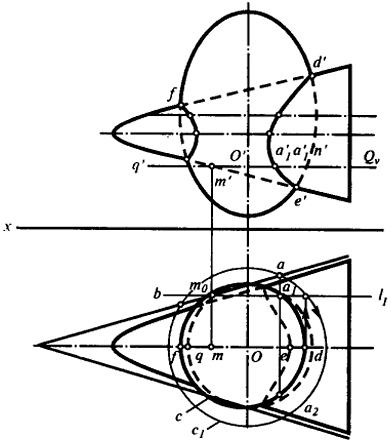
Рис. 135
Например, пусть требуется построить проекции линии пересечения поверхности трехосного гиперболоида с эллипсоидом вращения (рис. 135).
Для решения этой задачи проводим вспомогательную секущую плоскость Q, параллельную Н. Плоскость Q пересекает гиперболоид по гиперболе с вершиной в точке М (т, т'), а эллипсоид - по окружности с радиуса ON (o'n').
Преобразуем гиперболу в асимптоту, а окружность с в концентрическую окружность с1.
Для этого достаточно вначале построить асимптоту гиперболы горизонтального очерка гиперболоида; на ней находим точку т0 пересечения перпендикуляра, восставленного из точки т к оси горизонтальной проекции гиперболы.
Через точку т0 проводим граничную прямую l1. Окружность с преобразуется в окружность с1. Точки пересечения окружности с1 с асимптотой дают точки а и b. Обратным преобразованием находим положение точек а1 и a2, принадлежащих линии пересечения (точка b преобразуется в мнимые точки). Аналогично находим и другие точки линии пересечения.
М.А. Зайденварг [12] предлагает своеобразный способ задания квадратичных преобразований.
145
 |
 |
| Рис. 136 |
Рис. 137
|
При составлении алгоритма решения задач по определению линий пересечения некоторых поверхностей М.А. Зайденварг исходит из теоремы о том, что кривая второго порядка (α) устанавливает соответствие между двумя пучками: пучком поверхностей конусов вращения (Ω), вершина которых лежит в фокусе кривой, а ось перпендикулярна (плоскости кривой, и пучком плоскостей (Р), носителем которого служит директриса кривой (α) и вытекающих из этой теоремы следствий:
- 1) из трех элементов рассматриваемого соответствия (кривой α, конуса Ω и плоскости Р) любые два определяют третий;
- 2) кривая α может быть построена как ортогональная проекция линии пересечения Ω и Р на плоскость, перпендикулярную оси конуса.
Проследим на конкретных примерах за характером геометрических построений, которые необходимо выполнить для вычерчивания кривой второго порядка.
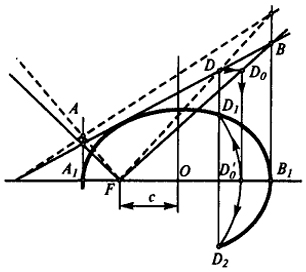
Пусть требуется построить эллипс по заданной оси 2а и фокусному расстоянию с (рис. 136).
По первому следствию, кривая α (в нашем случае эллипс) определяется конической поверхностью Ω и плоскостью Р и по второму следствию может быть построена как ортогональная проекция линии пересечения Ω × Р на плоскость, перпендикулярную оси конуса.
Для вычерчивания эллипса геометрические построения выполняем в следующей последовательности.
На горизонтальной прямой откладываем отрезок А1В1, равный 2а. Определяем один из фокусов эллипса (F), для чего от середины отрезка откладываем влево (или вправо) величину фокусного расстояния с.
146
Принимаем точку F за вершину поверхности конуса вращения с произвольным углом наклона образующих. Из точек А1 и В1 восставляем перпендикуляры к прямой A1B1 и отмечаем точки А и В их пересечения с очерковыми образующими конической поверхности. Прямая АВ определяет след фронтально-проецирующей плоскости, принадлежащей пучку Р. Эллипс строим как горизонтальную проекцию линии пересечения этой плоскости с поверхностью конуса. Для этого из произвольной точки D отрезка АВ проводим две прямые: одну - горизонтальную, вторую - перпендикулярную ей. Отмечаем точку D0 пересечения горизонтальной прямой с правой очерковой образующей конуса; из D0 опускаем перпендикуляр на отрезок А1В1. Через полученную точку D'0 проводим дугу окружности из центра F и отмечаем точки D1 и D2 ее пересечения с вертикальной прямой, которые принадлежат эллипсу. Аналогично находим другие точки эллипса.
Следует отметить, что эллипс можно построить и с помощью другой соответствующей пары конус - плоскость (на чертеже штриховыми линиями показаны конус Ω' и плоскость Р').
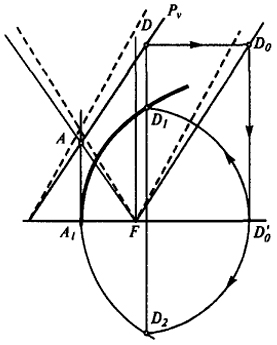
На рис. 137 показано построение параболы по заданной вершине А1 и фокусному расстоянию A1F.
Построения выполнены в следующей последовательности.
Принимаем точку F за вершину поверхности конуса вращения. Находим на очерковой образующей этой поверхности точку А(АА1 ⊥ A1F). Через точку А проводим след секущей плоскости Р параллельно правой образующей конуса. Из произвольной точки D, как и в предыдущем примере, проводим две взаимно перпендикулярные прямые. Находим точки D0 и D'0 из фокуса F проводим дугу радиусом FD'0 до пересечения ее с вертикальной прямой. Точки D1 и D2 принадлежат параболе. Таким же путем можно получить достаточное количество точек, принадлежащих параболе.
Как и в случае построения эллипса, парабола D1A1D2 может быть построена с помощью другого сочетания конической поверхности и плоскости. На чертеже штриховыми линиями показаны поверхность конуса Ω' и секущая P'.
Рассмотренное соответствие может быть использовано для решения задач по построению линии пересечения двух поверхностей, если их плоскими сечениями являются софокусные кривые второго порядка. Построение линии пересечения можно выполнить без вычерчивания кривых, получающихся в сечении.
147
1
Эллипс и окружность, как и всякая кривая второго порядка, преобразуются (распадаются) в две прямые, симметричные оси преобразования. На рис. 128 вторая пара прямых не показана.
