Все предыдущие примеры рассматривались для того, чтобы показать возможность преобразования прямой (точнее, двух прямых, расположенных симметрично относительно оси симметрии преобразования) в кривую второго порядка. В результате проведенных преобразований вместо прямых получали кривую.
Очевидно, практический смысл будут иметь такие преобразования, при которых кривую можно превратить в соответствующую пару прямых. Выполнив такое преобразование, задачу по нахождению точек пересечения кривых можно свести к нахождению точек, в которых пересекаются полученные прямые. Затем путем квадратичного преобразования находим точки пересечения заданных кривых. Сами кривые при этом можно не вычерчивать. Следует иметь в виду, что определение точек пересечения двух кривых второго порядка путем нахождения и последующего преобразования точек пересечения соответствующих прямых возможно только для кривых, имеющих общий фокус и совпадающие оси.
Пример. Определить точки пересечения эллипса с окружностью. Эллипс задан величиной и положением большой и малой оси; окружность - величиной радиуса и центром окружности, который совпадает с одним из фокусов эллипса (рис. 127).
Преобразуем эллипс и окружность в прямые. Такое преобразование может быть осуществлено, если графические построения, свойственные квадратичным
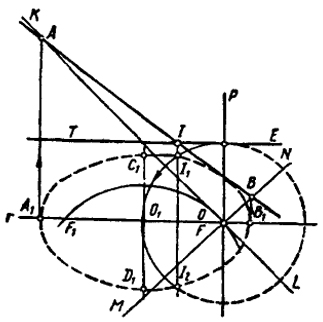
Рис. 127
137
преобразованиям (см. рис. 117), выполнить в обратном порядке.
За центр преобразования О принимаем точку F-общий фокус кривых. Ось симметрии преобразования должна совпасть с большой осью эллипса. Через центр О проводим двойную прямую p перпендикулярно оси симметрии и граничные прямые MN и KL. Теперь не составляет труда преобразовать эллипс и окружность в прямые.
Для нахождения точек А, В и А, В прямых, в которые преобразуется эллипс, из концов большой оси эллипса проводим прямые, параллельные двойной прямой до пересечения их с граничными прямыми.
Окружность преобразуется в прямые ТЕ и T E, параллельные оси симметрии преобразования и пересекающие двойную прямую в точках, отстоящих от центра на расстоянии радиуса окружности (на рис. 127 прямые А В и Т Е не показаны).
Преобразовывая точку I, в которых прямая АВ пересекается прямой ТЕ, получим искомые точки I1 и I2 пересечения эллипса с окружностью.
Мы видим, что точки пересечения двух кривых второго порядка найдены с помощью прямых линий без построения кривых1.
Приведенный пример составляет основу геометрических построений при решении задач по определению линий пересечения поверхностей методом квадратичных преобразований.
138
1
На рис. 127 окружность и эллипс показаны для наглядности штриховыми линиями.
