§ 33. Квадратичное преобразование прямой

Из свойства квадратичного преобразования следует, что при определенных условиях прямая может быть преобразована в кривую линию.

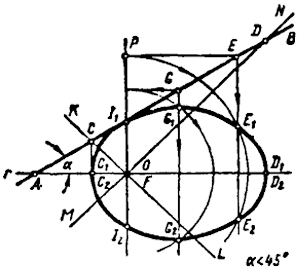
Действительно, точки С и D произвольной прямой АВ, лежащей в плоскости Q, преобразуются в совпадающие точки С₁С₂ и D₁D₂ (рис. 121).

Рис. 121	Рис. 122

134

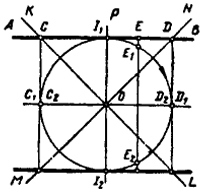
Рис. 123

Любая точка Е, лежащая на прямой АВ в интервале CD, преобразуется в две действительные точки Е₁ и E₂. Точки, расположенные на прямой АВ, левее точки С и правее точки D, преобразуются в мнимые. Следовательно, отрезок прямой CD может быть преобразован в замкнутую кривую, в частном случае, в эллипс или окружность.

Если угол наклона прямой АВ к оси симметрии меньше 45°, то такая прямая имеетнесобственные точки в областях мнимых точек преобразования. Как известно, кривая второго порядка, обладающая только мнимыми несобственными точками, является эллипсом¹ (рис. 122).

Если прямая параллельна оси симметрии, то как это ясно из рис. 123, она преобразуется в окружность.

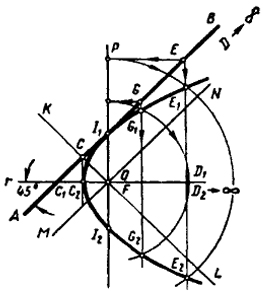
Если прямая составит с осью симметрии угол ± 45°, то такая прямая преобразуется в параболу (рис. 124). Действительно, заданная прямая пересекает одну из граничных прямых (MN) в несобственной точке, которая преобразуется в несобственную вершину кривой. Вторая вершина кривой определится преобразованием точки С, в которой заданная прямая АВ пересекает другую граничную прямую (KL).

Рис. 124	Рис. 125

135

Если прямая составляет с осью симметрии угол больше 45°, то она преобразуется в гиперболу (рис. 125). Это следует из того, что прямая АВ имеет несобственную точку в области действительных точек преобразования, поэтому она преобразуется в кривую второго порядка с двумя действительными несобственными точками, т.е. гиперболу.

Следует подчеркнуть, что рассмотренные преобразования прямой в различные кривые второго порядка возможны лишь в частных случаях преобразования. Необходимым условием такого преобразования является совпадение оси симметрии и центра преобразования с осью и фокусом кривой.

136