Основу квадратичного способа составляет преобразование следующего вида.
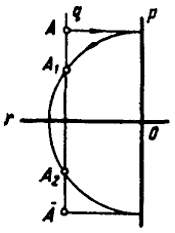
Пусть произвольная точка А пространства лежит в плоскости Q (рис. 117).
Через произвольную точку о этой плоскости проведем две взаимно перпендикулярные прямые r и р. Через точку А проведем прямую q, параллельную прямой р. Из точки о опишем окружность радиусом, равным расстоянию от точки А до прямой r.
Будем считать, что каждая точка плоского поля преобразуется в точки, в которых эта окружность пересекает прямую q.
В общем случае каждой точке А плоскости Q будут соответствовать две точки А1 и А2, также лежащие в этой плоскости. Из чертежа видно, что в плоскости Q существует еще одна точка A, которая преобразуется в те же точки А1 и A2.
Построения, выполненные на рис. 117, обеспечивают взаимнодвузначное преобразование. Это преобразование будет вполне определено, если заданы точка о - центр преобразования и одна из прямых - двойная прямая (в нашем случае совпадающая с прямой р) или ось симметрии преобразования (прямая, совпадающая с прямой r).
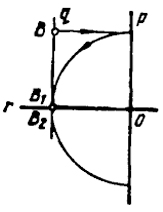
Следует отметить, что точка В или В, равноудаленная от двойной прямой р и оси симметрии r, т.е. лежащая на прямых, проходящих через центр преобразования о и составляющих с прямыми p и r углы в 45°, преобразуется в две совпадающие точки В1 и B2, лежащие на оси симметрии (рис. 118).
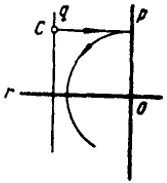
Любая точка С, расстояние которой от двойной прямой больше, чем от оси симметрии, преобразуется в мнимые точки (рис. 110).
Приведенные чертежи показывают, что квадратичное преобразование позволяет, в зависимости от положения точки на плоскости, получить соответствующие ей две действительные различные точки
 |
 |
 |
| Рис. 117 |
Рис. 118 |
Рис. 119 |
133
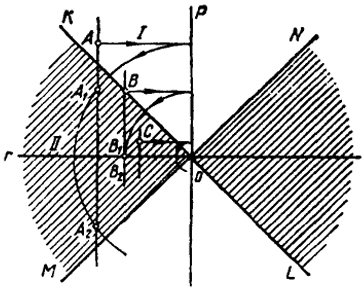
Рис. 120
(рис. 117); две действительные совпадающие точки (рис. 118) и мнимые точки (рис. 119).
На рис. 120 показаны две области I и II. Любая точка области I преобразуется в две действительные точки; любая точка области II преобразуется в мнимые точки. Точки, лежащие на границе этих областей (прямых MN и KL), преобразуются соответственно в две действительные совпадающие точки.
134
