Преобразование кривой линии в проецирующую прямую (см. рис. 112) является основой графических построений при решении задач способом топологических преобразований по определению точки встречи произвольной линии с нелинейчатой поверхностью.
Действительно, если с помощью сочетания конической и плоской поверхностей преломления можно преобразовать кривую линию в отрезок проецирующей прямой, то, рассматривая произвольную поверхность как состоящую из множества кривых образующих, можно преобразовать каждую из этих образующих в проецирующие прямые, совокупность которых определит проецирующую поверхность1.
На рис. 113 показана произвольная (топографическая) поверхность. Эту поверхность можно рассматривать как совокупность бесчисленного количества плоских кривых горизонталей.
Преобразуя каждую из горизонталей в фронтально-проецирующую прямую, мы сможем преобразовать топографическую поверхность в поверхность проецирующую.
На чертеже выполнены построения для преобразования горизонталей I, II, III и ABC. Построения выполнены аналогично рассмотренным на рис. 112.
Следует иметь в виду, что если угол наклона плоскости преломления Q2 к плоскости проекции H будет равен углу наклона к этой же плоскости образующей конической поверхности, параллельной фронтальной плоскости проекции, то направляющая цилиндрической поверхности будет конгруентна фронтальной проекции очерка преобразованной поверхности.
На рис. 113 штриховыми линиями показаны фронтальный след Q2v проецирующей плоскости преломления, параллельной образующей конуса SI, и фронтальная проекция цилиндрической поверхности. Из чертежа видно, что кривая 1'2, d'1, 2'2,3'2, 4'2 параллельна исходной кривой 1', b', 2', 3', 4'.
Теперь остановимся на решении задачи по определению точек встречи произвольной кривой с произвольной поверхностью.
Ход решения такого типа задач способом топологических преобразований рекомендуется следующий:
- 1) преобразовываем заданную поверхность в проецирующую;
- 2) по этому же закону преобразовываем линию;
125
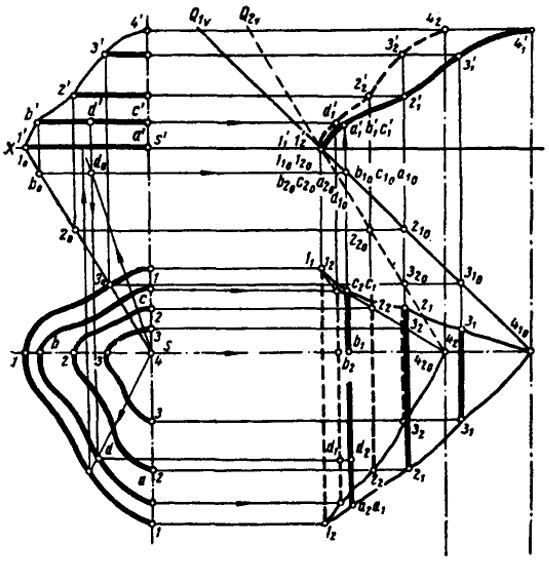
Рис. 113
- 3) находим точки пересечения проекций линий и поверхности в преобразованном положении;
- 4) обратными лучами возвращаем полученные точки на исходные проекции.
Задача 1. Определить точки встречи произвольной кривой АВ с поверхностью эллиптического параболоида (рис. 114).
Преобразуем поверхность эллиптического параболоида в проецирующую цилиндрическую поверхность. Проще всего можно ее преобразовать в параболический цилиндр. Для этого достаточно фронтальную проекцию очерка данной поверхности принять за направляющую цилиндрической поверхности, а ее криволинейные образующие преобразовать в отрезки прямых, перпендикулярных фронтальной плоскости проекций.
В качестве криволинейных образующих берем горизонтали поверхности, а для их преобразования воспользуемся конической поверхностью отражения в пространстве Π и плоскостью отражения в преобразованном пространстве Π1. За направляющую конической поверхности нужно принять горизонтальную проекцию очерка эллиптического
126
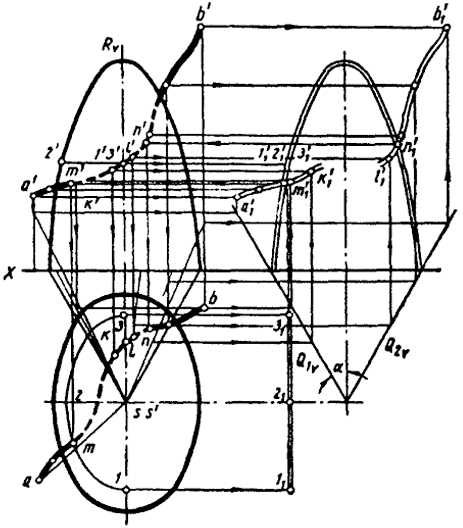
Рис. 114
параболоида; вершину S можно взять в произвольной точке прямой, проходящей через вертикальную ось симметрии заданной поверхности.
Направление фронтального следа Q1v плоскости преломления должно быть параллельным левой очерковой образующей конической поверхности.
Не следует забывать, что при топологических преобразованиях должен быть выдержан принцип взаимной непрерывности, который, как уже отмечалось, не допускает разрывов линий и поверхностей.
В нашем случае приходится преобразовывать замкнутые кривые (эллипсы) в две прямые. Очевидно, топологически такие преобразования не могут быть осуществлены.
Чтобы применение топологических преобразований стало возможным, мысленно рассекаем поверхность заданного параболоида плоскостью R, перпендикулярной X и проходящей через его ось симметрии. Теперь можно применить способ топологических преобразований, причем для преобразования части поверхности, расположенной левее плоскости R, и для участка кривой АК следует воспользоваться
127
левой частью конической поверхности преломления и соответствующей ей плоскостью преломления Q1.
Для образования правой части поверхности и участка кривой LB нужно пользоваться правой частью конической поверхности преломления и плоскостью преломления Q2.
При принятом нами аппарате преобразования каждая из криволинейных образующих эллиптического параболоида, параллельная горизонтальной плоскости проекций, преобразуется в две прямые, перпендикулярные плоскости V, а сама поверхность - в проецирующую цилиндрическую. Кривая АВ - в две кривые А1К1 и L1B1.
Все построения выполнены аналогично ранее разобранным на рис. 113.
Точки m'1 и n'1 в которых фронтальные проекции преобразованных участков кривой a'1k'1 и l'1b'1 пересекают фронтальный след цилиндрической поверхности, будут искомыми в преобразованном положении. Точки т' и n', в которых прямые, проведенные параллельно оси X, пересекают фронтальную проекцию кривой а'1b'1, являются фронтальными проекциями искомых точек встречи. По т' и п' определяем m и n.
В этой задаче, как и во всех ранее разобранных примерах, мы смещали преобразованное пространство вправо.
Делалось это для того, чтобы избежать наложения новых преобразованных проекций на старые исходные и не затруднять чтение чертежа. Теперь, когда мы подробно разобрали характер графических построений, присущих способу топологических преобразований, можно не делать такого смещения, а преобразовывать пространство "само в себя". Это дает возможность значительно сократить количество графических построений.
С точки зрения топологии, такое преобразование будет более оправданным. Действительно, топология предусматривает деформацию пространства, а не перемещение его в новое положение.
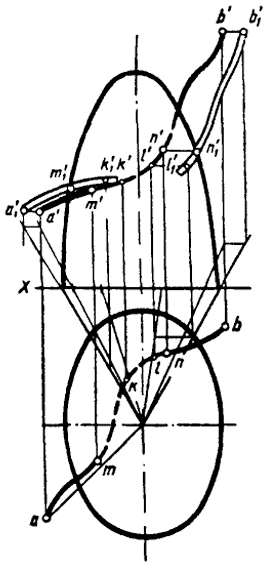
На рис. 115 показано решение предыдущей задачи путем преобразования пространства "само в себя".
Фронтальный след цилиндрической поверхности совпадает с фронтальным очерком поверхности параболоида. Ветви кривой АК и LB преобразуются в кривые А1К1 и L1B1. Пересечение а'1k'1 и 1'1b'1 с фронтальным следом цилиндрической поверхности определит проекции точек встречи т'1 и п'1 в преобразованном положении.
Для нахождения проекций т'п' достаточно через т'1 и п'1 провести прямые, параллельные X, до пересечения их с кривой а'b'.
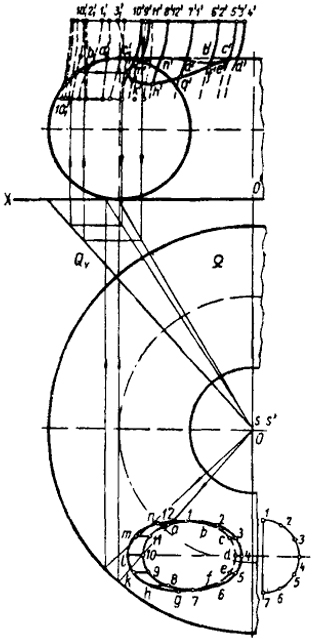
Задача 2. Найти линию пересечения поверхностей кольца и эллиптического цилиндра с изогнутой осью (рис. 116).
128
 |
 |
| Рис. 115 |
Рис. 116 |
С помощью топологического способа преобразуем кольцевую поверхность в поверхность прямого кругового цилиндра, перпендикулярного плоскости V.
Преобразование осуществляем посредством конической поверхности преломления Ω и плоскости Q. За направляющую конической поверхности принимаем горизонтальную проекцию очерка кольца; за вершину - произвольную точку S, лежащую на оси кольца. След Qv фронтально-проецирующей плоскости преломления должен совпадать с очерковой образующей конуса.
Выбранное положение следа Qv обеспечит преобразование исходного пространства "само в себя". При таком виде и расположении преобразующих поверхностей преломления кольцевая поверхность преобразуется в круговую цилиндрическую, фронтальная проекция которой совпадает с окружностью сечения кольца плоскостью, параллельной V и проходящей через центр кольцевой поверхности.
129
Образующие цилиндрической поверхности преобразуются в плоские кривые I1, II1, III1 и т.д.
На чертеже стрелками показано построение образующей цилиндра X1. Точки а'1, b'1, c'1, в которых фронтальные проекции этих кривых пересекают окружность (фронтальную проекцию преобразованной кольцевой поверхности), будут фронтальными проекциями искомых точек в преобразованном положении.
Точки а', b', с' находим пересечением прямых, параллельных оси X и проведенных через точки а'1, b'1, c'1 … с соответствующими фронтальными проекциями образующих эллиптического цилиндра.
По фронтальным проекциям а', b', с' определяем их горизонтальные проекции.
Соединив одноименные проекции в определенной последовательности, получим проекции искомой линии пересечения.
Приведенные примеры показывают, что способ топологических преобразований позволяет значительно упростить решение сложных задач.
В ряде случаев этот способ является единственно возможным способом точного решения сложных задач.
130
1
Кривые образующие должны быть подобными и подобно расположенными.
