Из рис. 109 следует, что угол наклона плоскости Q1 к горизонтальной плоскости проекции H определяет интенсивность деформации пространства. Причем, если этот угол постоянный, то окажется постоянной и интенсивность деформации.
Поэтому, принимая в качестве взаимно соответствующих поверхностей преломления плоскости Q и Q1, мы предрешаем деформацию
119
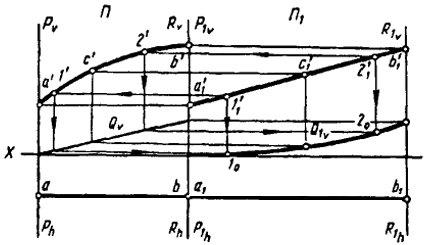
Рис. 110
растяжения или сжатия, равномерную по всему объему преобразуемого пространства. Следовательно, с помощью плоскостей преломления нельзя преобразовать криволинейные формы (линии и поверхности) в прямолинейные.
Чтобы преобразовать кривую линию или поверхность с криволинейными образующими в прямые линию или поверхность, необходимо осуществить неравномерную деформацию пространства, в котором находится заданная фигура.
Такая деформация может быть получена, если взять вместо плоскости преломления Q1 произвольную цилиндрическую поверхность (для упрощения последующих построений поверхность следует брать проецирующей).
Углы наклона цилиндрической поверхности к плоскости Н в различных точках, не лежащих на одной прямой, перпендикулярной V, будут отличаться один от другого, т.е. деформация пространства будет неравномерной.
Характер кривой Q1v (фронтального следа цилиндрической поверхности) определяет интенсивность деформации отдельных участков пространства. Следовательно, чтобы преобразовать плоскую кривую линию в прямую, необходимо в качестве поверхностей преломления в преобразованном (или исходном) пространстве взять цилиндрическую поверхность.
На рис. 110 показано топологическое преобразование кривой АСВ в прямолинейный отрезок А1В1. Необходимые построения выполняются в следующей последовательности.
Ограничиваем пространство Π, в котором находится кривая АСВ, плоскостями Р и R. Преобразовываем пространство Π в Π1. Границы деформированного пространства отмечены плоскостями Р1 и R1.
Проекции деформированного пространства можно изобразить в любом месте чертежа. Располагаем эти проекции так, чтобы правая
120
плоскость R исходного пространства совпала с левой плоскостью Р1 преобразованного пространства.
В пространстве Π проводим преобразующую плоскость преломления Q. Для упрощения построений плоскость Q принята фронтально-проецирующей. Чтобы построить проекции прямой, в которой преобразуется кривая АСВ, достаточно иметь преобразованное положение двух точек этого отрезка.
В качестве таких точек можно принять точки А1 и В1, которые независимо от вида преобразующих поверхностей преломления будут однозначно соответствовать точкам А и В пространства Π.
Через точки А1В1 можно провести бесчисленное множество линий, соответствующих данной кривой. Характер этих линий будет определяться видом цилиндрической поверхности преломления, проведенной в пространстве. Очевидно, задав определенный вид направляющей цилиндрической поверхности, мы ответим на вопрос, какое очертание преобразованной линии будет соответствовать принятому виду цилиндрической поверхности преломления.
Но нас интересует не вид этой поверхности, которая является элементом аппарата преобразования, а конечный результат преобразования линии АСВ. Поэтому, возвращаясь к нашему примеру, следует вначале через точки А1 и В1 провести отрезок прямой, а затем с помощью обратных лучей построить направляющую цилиндрической поверхности преломления, которая обеспечит такое преобразование.
На рис. 110 показано построение только точек 10 и 20, принадлежащих следу поверхности Q1.
Рассмотренный пример показывает характерную особенность решения ряда задач начертательной геометрии способом топологических преобразований, которая состоит в том, что мы вначале задаем (вычерчиваем) преобразованный вид фигуры, а затем определяем характер поверхности преломления, который обеспечивает получение фигуры такого вида.
При использовании в качестве преобразующей поверхности преломления цилиндрической поверхности можно осуществить неравномерную деформацию пространства. Будут получены области сжатия и растяжения, причем их протяженность и интенсивность может изменяться в широком диапазоне. Таким образом, топологические преобразования с помощью цилиндрических поверхностей преломления являются более деформативными, чем преобразования, в которых используются плоскости преломления.
С помощью цилиндрической поверхности преломления нетрудно решать сложные задачи на определение линий пересечения поверхностей.
121
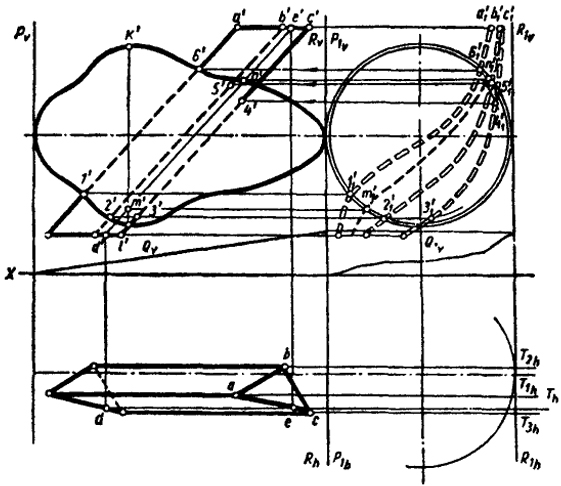
Рис. 111
В качестве примера, иллюстрирующего использование цилиндрической поверхности преломления для топологического преобразования геометрических фигур, найдем линию пересечения произвольной поверхности вращения с трехгранной призмой (рис. 111).
Графически решить эту задачу изложенными ранее способами трудно. Используя топологический метод, можно получить весьма простое решение. Для этого достаточно преобразовать данное тело вращения в шар. Чтобы осуществить такое преобразование, необходимо деформировать пространство Π, в котором находится тело вращения, в пространство Π1 путем неравномерного сжатия (при общей деформации сжатия некоторые участки деформированного пространства будут растянутыми).
Расстояние между плоскостями Р1 и R1 следует принять равным величине максимального диаметра KL тела вращения.
Так как очерк тела вращения представляет кривую произвольного вида, то для преобразования ее в окружность необходимо иметь цилиндрическую поверхность преломления, обеспечивающую неравномерное распределение деформации.
Характер направляющей линии этой поверхности легко определить после того, как будет построена фронтальная проекция шара.
122
Построение линии Q1v осуществляется аналогично построениям, описанным ранее в примере (см. рис. 110); с помощью поверхностей преломления Q и Q1 и взаимно перпендикулярных лучей преобразовываем ребра призмы в плоские кривые пространства Π1. Выполненными преобразованиями мы свели сложную задачу к простейшей.
Далее достаточно рассечь шар горизонтально-проецирующими плоскостями Т, проходящими через ребра призмы, и найти точки I, II, III, IV, V, VI, в которых преобразованные ребра призмы пересекаются с окружностями - линиями пересечения шара с плоскостями Т; обратными лучами переносим фронтальные проекции точек I, II, III, IV, V, VI на исходные проекции. Для точного построения линий пересечения каждой грани призмы в них следует провести дополнительные прямые и построить точки встречи этих прямых с заданной поверхностью.
На рис. 111 показаны построения, необходимые для получения дополнительных точек М и N прямой DE, взятой на грани АС.
Из чертежа видно, что для решения задачи достаточно построить в преобразованном пространстве только одни фронтальные проекции точек.
В связи с этим оказывается возможным сократить количество графических построений путем вычерчивания только фронтальных проекций.
На рис. 111 горизонтальная проекция криволинейной поверхности в исходном положении не показана. После преобразования показана только часть окружности экваториального сечения шара, в который преобразовано заданное геометрическое тело. Эта дуга нужна только для определения величины радиусов окружностей, по которым плоскости Т, проходящие через ребра призмы, рассекают поверхность шара.
123
