Топология рассматривается нами с точки зрения возможности ее использования, для преобразования заданных ортогональных проекций, с целью облегчения решения задач начертательной геометрии. Поэтому мы остановимся только на таких преобразованиях, которые можно легко осуществить графически.
С этой целью удобно рассматривать геометрическую фигуру неразрывно связанной с трехмерным пространством, в котором она находится.
В этом случае, преобразовывая (деформируя) пространство, мы будем преобразовывать и геометрическую фигуру. Очевидно, подвергая пространство различной деформации, можно произвольную геометрическую фигуру преобразовать в любую другую, по форме и свойствам наиболее удобную для решения данной конкретной задачи.
Как было отмечено раньше, сущность способа топологических преобразований состоит в том, что решение задачи осуществляется на
117
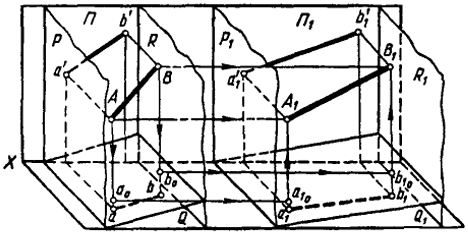
Рис. 108
преобразованном виде фигуры с последующим возвращением полученного результата на исходные ортогональные проекции.
Поэтому, чтобы сделать возможным практическое использование топологических преобразований, необходимо установить графически соответствие между точками преобразованного и исходного пространств.
Такое соответствие может быть легко осуществлено с помощью двух взаимно перпендикулярных лучей, проходящих через точку, и двух взаимно соответствующих поверхностей преломления.
Допустим, что отрезок общего положения АВ длиной L топологически преобразован в отрезок А1В1 длиной Z1 также общего положения. При этом удаление концов отрезка от плоскостей H и V (рис. 108) в исходном и преобразованном положении не изменяется (Аа = А1а1, Аа' = A1a'1 u Bb = B1b1, a Bb' = B1b'1). Такое преобразование можно осуществить путем равномерной деформации растяжения пространства Π, в котором находится отрезок, в Π1 по направлению оси X.
Для наглядности исходное пространство Π ограничено плоскостями Р и R, после деформации расстояние между плоскостями Р1 R1 увеличится1. Чтобы не затруднять чтения чертежа, преобразованное пространство Π1 на рис. 108 смещено вправо. Связь между точками пространства Π и Π1 осуществлена посредством двух взаимно перпендикулярных пучков лучей и двух взаимно соответствующих плоскостей преломления Q и Q1; одной Q - в исходном, другой Q1 - в преобразованном пространстве.
Для простоты построения плоскость Q взята перпендикулярно V. Угол наклона ее к плоскости H произвольный. Соответствующая ей
118
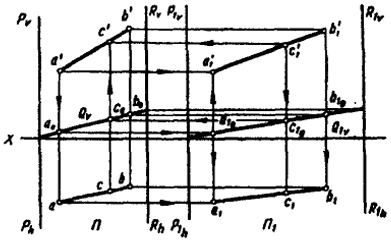
Рис. 109
плоскость Q1 деформированного пространства также фронтально-проецирующая.
Точке А исходного пространства соответствует точка А1 преобразованного пространства. Соответствие установлено с помощью лучей АА1 и Аа0. Луч АА1 параллелен плоскости H, a Aa0 перпендикулярен H. Второй луч встречается с плоскостью преломления Q в точке а0 и отражается от нее в пространство П1 в направлении, параллельном первому лучу АА1. В пространстве П1 второй луч встречается с плоскостью преломления Q1 в точке a10 и отражается от нее в направлении, перпендикулярном плоскости H.
Точка А1 лежит на пересечении первого луча с перпендикуляром, восстановленным из точки а10.
Аналогично находим точку В1. Соединив точку А1 с В1, получаем преобразованный вид отрезка АВ.
На рис. 109 все построения выполнены на эпюре. Здесь так же, как и на рис. 108, пространство П1 смещено вправо.
На этом же чертеже в качестве примера показано построение точки С в исходном пространстве, соответствующей точке С1 преобразованного пространства.
119
1
В случае, если расстояние между плоскостями
Р1 и
R1 окажется меньше расстояния между плоскостями
Р и
R, будет иметь место деформация сжатия.
