Топология происходит от греческих слов τοποζ - место и λογοζ - наука; в несколько вольном переводе топологию можно рассматривать как "геометрию положения".
Подойти к понятию топология можно путем следующих рассуждений.
Пусть нам задана прямоугольная трапеция ABCD. С точки зрения элементарной геометрии, этот геометрический образ будет характеризоваться длиной ее сторон, величиной углов при вершинах, площадью и другими метрическими свойствами.
Ортогональное проецирование трапеции ABCD на плоскость Р, параллельную плоскости трапеции, дает проекцию abcd, которая обладает теми же метрическими свойствами, какие присущи оригиналу (рис. 103).
Проективная геометрия показывает, что эти метрические характеристики оказываются чрезвычайно неустойчивыми и исчезают при проекционном преобразовании (за исключением случая, рассмотренного на рис. 103). Действительно, спроектировав параллельно трапецию ABCD на произвольную плоскость Р (рис. 104), мы получим проекцию abcd, у которой длины сторон, величины углов и площадь будут отличаться от соответствующих метрических характеристик заданной трапеции.
114
 |
 |
| Рис. 103 |
Рис. 104 |
При таком проекционном преобразовании сохраняется параллельность сторон оснований трапеций, такие преобразования известны под названием перспективно-аффинных или родственных.
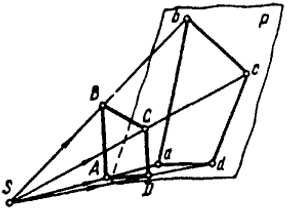
Если проецирование трапеции на плоскость Р осуществить из какого-либо центра S, т.е. подвернуть ее гомологическому преобразованию (рис. 105), то окажется, что новая проекция abcd не сохранит ни одного из метрических свойств, присущих оригиналу. В том числе нарушается и параллельность прямых.
Следовательно, параллельность сторон нарушается при гомологичном преобразовании фигуры; при аффинном преобразовании нарушаются углы и относительные размеры отдельных частей фигуры.
Еще менее стойкими оказываются абсолютные размеры фигуры - они сохраняются лишь при конгруентных преобразованиях.
Рассмотренные примеры показывают, что при проекционных преобразованиях метрические свойства, в силу их непостоянства, не могут служить основанием для глубокого изучения заданного геометрического образа, подвергающегося проективным преобразованиям.
Будем считать более существенными те геометрические свойства, которые остаются неизменными при различных проективных преобразованиях.
С этой точки зрения, проективные свойства оказываются более важными, чем метрические, но, как будет показано ниже, можно осуществить такое преобразование геометрического образа, при котором исчезают и проективные свойства. Желание выделить из геометрических свойств наиболее важные - самые стойкие свойства геометрического образа, способные выдержать различные преобразования, приводят к топологическим свойствам.
Топологическими свойствами называют свойства, которые не нарушаются ни при каких взаимно-однозначных и взаимно-непрерывных преобразованиях.
Отмеченные свойства могут быть получены, если преобразовать фигуру Φ в фигуру Φ1, соблюдая при этом два условия:
115
 |
 |
| Рис. 105 |
Рис. 106 |
- 1) каждой точке исходной фигуры будет соответствовать одна и только одна точка преобразованной фигуры Φ1 - взаимная однозначность;
- 2) бесконечно близким точкам исходной фигуры Φ будут соответствовать также бесконечно близкие точки преобразованной фигуры Φ1 - взаимная непрерывность.
Такие взаимно-однозначные и взаимно-непрерывные преобразования называются топологическими преобразованиями.
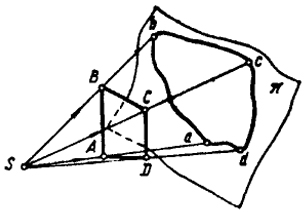
С проективной точки зрения, топологическое преобразование рассматриваемой трапеции ABCD можно представить как центральное проецирование ее на произвольную поверхность π (рис. 106).
Отсюда видно, что топологические преобразования не сохраняют даже прямолинейности линий.
При топологических преобразованиях мы можем заданную фигуру подвергать произвольной деформации, следя лишь затем, чтобы не происходило разрывов и склеивания линий или поверхности фигуры; иными словами, чтобы не нарушался принцип взаимной непрерывности и взаимной однозначности.
Исходя из этого, любая простая (не имеющая двойных точек) замкнутая кривая топологически может быть преобразована в окружность, эллипс и т.д.).
Произвольная замкнутая поверхность может быть преобразована в любую другую замкнутую поверхность.
Геометрическое тело, ограниченное произвольной криволинейной поверхностью, может быть преобразовано в куб, шар, цилиндр, конус и т.д. Следует иметь в виду, что топологическое преобразование одной фигуры в другую возможно только между гомеоморфными фигурами, принадлежащими к одному топологическому типу1.
116
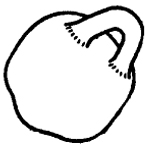
Рис. 107
Так, шар и цилиндр могут быть топологически преобразованы друг в друга. Но тор уже не может быть преобразован в цилиндр так же, как и цилиндр в тор, так как в первом случае нам пришлось бы в каком-то месте разрезать поверхность тора (нарушится взаимная непрерывность); во втором - склеить поверхность цилиндра (не обеспечивается взаимная однозначность).
В то же время тор может быть преобразован в произвольную фигуру типа, изображенного на рис. 107, или в цилиндр с отверстием.
При всех этих преобразованиях поверхность, ограничивающую геометрическую фигуру, следует рассматривать как прочную эластичную пленку, способную изгибаться, растягиваться, сжиматься, но не рваться и не склеиваться.
Топологические преобразования обладают чрезвычайно широкими возможностями в смысле деформативности. С этой точки зрения, использование их для решения задач начертательной геометрии является весьма эффективным особенно в тех случаях, когда приходится иметь дело с геометрическими телами, ограниченными нелинейчатыми поверхностями.
117
1
Александров П.С.,
Ефремович В.А. "О простейших понятиях современной топологии". ОНТИ, 1935.
