Для упрощения решения задач, помещенных в предыдущем параграфе, использовалось, по существу, сочетание способа проективных преобразований со способом вспомогательного проецирования (параллельного на рис. 98 и 99 и центрального на рис. 100 и 101).
В ряде случаев решение задачи методом проективных преобразований можно значительно упростить, если принять такой план решения, который предусматривает использование на каком-то этапе решения классических способов преобразования.
Приведенные на рис. 86, 87 задачи показывают, что использование способа проективных преобразований целесообразно лишь в тех случаях, когда оси фигур, ограниченных нелинейчатыми поверхностями второго порядка, занимают проецирующее положение по отношению к плоскостям проекций.
Очевидно, в тех случаях, когда эта ось общего положения, целесообразно, чтобы применению способа проективных преобразований предшествовал способ, с помощью которого можно заданный эпюр привести к виду, наиболее удобному для применения проективного способа.
Для осуществления операции преобразования фигуры, занимающей произвольное положение в пространстве, в положение, при котором ее ось будет перпендикулярной плоскости проекций, целесообразно использовать классические способы - перемены плоскостей проекций или параллельного перемещения.
В некоторых задачах бывает целесообразно вначале осуществить проективные преобразования, а затем использовать один из классических методов. Сочетание способа проективных (гомологических) преобразований со способом вращения (совмещения) рассмотрено выше (см. рис. 96).
Разберем на примере построения линий касания конической поверхности с поверхностью трехосного эллипсоида практическую целесообразность использования одновременно двух способов преобразования - проективного, в частности - перспективно-аффинного, и классического - перемену плоскостей проекций (рис. 102). При помощи родственного преобразования трехосный эллипсоид может быть преобразован в шар диаметром, равным средней оси эллипсоида1.
110
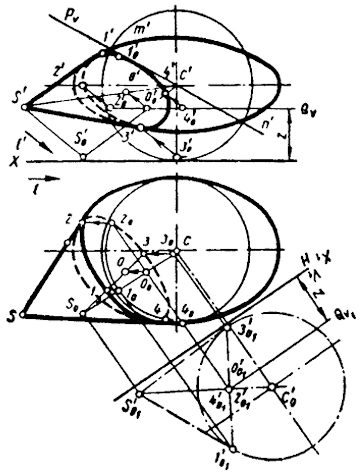
Рис. 102
Из точек сс' проводим проекции шара, родственного заданному эллипсоиду. Двойные точки М и N (на чертеже показаны только их фронтальные проекции) определяют фронтальный след Pv двойной (родственной) плоскости преобразования. Направление преобразования L определяется положением образующей цилиндрической поверхности, касательной к шару и эллипсоиду. Имея Pv и l, l', находим преобразованное положение вершины конуса S0.
Искомой касательной конической поверхности в преобразованном пространстве будет соответствовать круговой конус с вершиной S0. Его линия касания к шару, как известно, будет окружность. В общем случае она спроецируется на Н и V в виде эллипсов, сопряженные диаметры которых легко определить, пользуясь заменой фронтальной плоскости проекции V на V1. Плоскость V1 принимаем параллельной оси кругового конуса.
Линия касания (окружность) проецируется на V1 в виде отрезка прямой 1'013'01. Проекции взаимно перпендикулярных диаметров этой окружности на V1 будут 1'013'01 и 2'014'01.
111
Горизонтальные проекции точек О0 и 10, 30 находятся на горизонтальной проекции s0c, а точки 20 и 40 на окружности, по которой шар рассекается плоскостью Q. Зная положение точек О0, 10, 20, 30, 40, не составляет труда найти 0, 1, 2, 3, 4, а по ним и фронтальные проекции этих точек. Направление построений указано стрелками.
Точки I, III и II, IV являются концами сопряженных диаметров эллипса, по которому происходит касание заданного конуса с трехосным эллипсоидом. По проекциям этих точек строим проекции эллипса.
112
1
Четверухин Н.Ф. "Высшая геометрия". Учпедгиз. М., 1939.
