§ 23. Гомотетические преобразования

Параллельность прямых, как известно, не является инвариантом гомологических преобразований. В общем случае гомологии прямые, параллельные до преобразования, после преобразования не сохраняют этого свойства.

Графически гомология может быть легко представлена как центральное проектирование плоской фигуры с одной плоскости Р на другую Q. Соответственные прямые пересекаются между собой на оси гомологии, которая является линией пересечения плоскостей Р и Q.

Если фигуру, расположенную в плоскости Р, проектировать из центра S на плоскость Q, параллельную Р, то линия пересечения плоскостей (ось гомологии) в этом случае является несобственной прямой. Следовательно, соответственные прямые должны быть параллельными, так как они будут пересекаться в точках несобственной оси.

Рассматриваемый нами частный случай гомологии называется гомотетия.

Гомотетия является ничем иным, как преобразованием подобия, при котором центром подобия является центр гомологии. Иначе гомотетия - гомология с несобственной осью и собственным центром.

Основным свойством гомотетии является постоянство отношения отрезков соответствующих прямых. Это отношение называется также коэффициентом гомотетии.

Гомотетия преобразует каждую фигуру в подобную и подобно расположенную, поэтому коэффициент гомотетии представляет собой коэффициент подобия.

100

Использование свойств гомотетии дает возможность упростить решение некоторых задач по определению линий пересечения поверхностей.

В гомотетическом способе, который в дальнейшем, для простоты, будем называть способом подобия, использована известная теорема Монжа о двойном касании.

Как известно, эта теорема утверждает, что "всякие две поверхности второго порядка, имеющие двойное касание, пересекаются между собой по двум плоским кривым второго порядка".

Прежде чем перейти к изложению способа подобия, отметим некоторые следствия, которые вытекают из теоремы Монжа.

1. Если две поверхности второго порядка вписаны или описаны около третьей поверхности второго порядка, то они пересекаются между собой по плоским кривым.
2. Если кривой пересечения поверхностей является эллипс, то всегда можно найти направление проецирования, при котором эллипс спроецируется на плоскость, перпендикулярную к этому направлению, в окружность.
3. Кривые второго порядка, получаемые в результате сечения поверхности второго порядка параллельными плоскостями, подобны.
4. Две подобные и подобно расположенные поверхности второго порядка рассекаются параллельными плоскостями по подобным и подобно расположенным кривым.

В качестве примера определения направления параллельного проецирования, при котором эллипс спроецируется в окружность, рассмотрим следующую задачу.

Пусть прямой круговой конус S рассекается фронтально-проецирующей плоскостью Р (рис. 97). Натуральная величина большой оси эллипса равна отрезку а'b'. Малая ось равняется отрезку cd. Из точки о' описываем окружность радиусом, равным половине величины малой оси эллипса cd. Направление фронтальной проекции проецирования совпадает с направлением касательных, проведенных из концов большой оси эллипса - точек а', b' к этой окружности. Плоскость R, на которую эллипc

Рис. 97

101

спроецируется в окружность a₁b₁c₁d₁, должна быть перпендикулярна к полученному направлению проецирования b'b₁.

Отмеченные в пп. 1-4 свойства дают возможность решать позиционные задачи по определению линий пересечения двух поверхностей второго порядка.

Сущность решения задач способом подобия состоит в следующем.

Если заданы две поверхности второго порядка Ψ и Ω, линию пересечения которых требуется определить, то в свободном месте чертежа строим подобные и подобно расположенные поверхности Ψ и Ω, описанные около шаровой поверхности. Эти поверхности пересекутся по двум плоским кривым I₁ и II₁.

По свойствам подобия фигуры Ψ и Ω будут пересекаться по кривым I и II, подобным I₁ и II₁. Для определения точек, принадлежащих этим кривым, можно (на основании следствия 4) воспользоваться вспомогательными секущими плоскостями, параллельными плоскостям, в которых расположены кривые I₁ и II₁.

Если хотя бы одна из кривых, по которым пересекаются поверхности, Ψ и Ω - эллипс, то вспомогательную плоскость Q следует проводить параллельно плоскости этого эллипса. В этом случае плоскость Q рассечет поверхности Ψ и Ω также по эллипсам, подобным и подобно расположенным эллипсу, параллельно плоскости которого проводились вспомогательные плоскости (на основании следствия 3).

Теперь, получив в сечении эллипс, мы можем выбрать такое направление проецирования и соответственно вспомогательную плоскость проекций, на которую он спроецируется в окружность (см. следствие 2).

Рассекая поверхности Ψ и Ω рядом плоскостей Q₁, Q₂, Q₃ и т.д., получим несколько пар эллипсов сечения и соответственно несколько пар окружностей.

Точки, в которых пересекаются окружности, являются вспомогательными проекциями точек кривой линии пересечения.

Обратными лучами переносим эти точки на основные проекции; соединив одноименные проекции в определенной последовательности плавными кривыми, получим проекции искомых кривых.

Ход решения задач и характер графических построений при их решении способом подобия проследим на примере следующих задач.

Задача 1. Определить линию пересечения двух конусов вращения со скрещивающимися осями (рис. 98)¹.

102

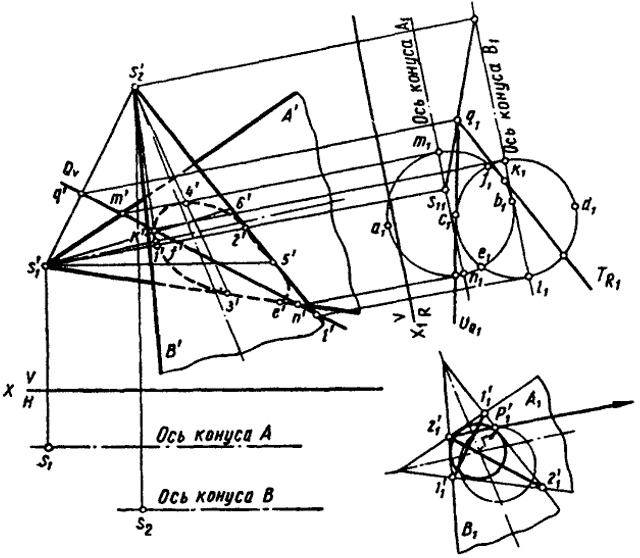
Рис. 98

В свободном месте чертежа строим шар произвольного радиуса.

Затем описываем около него конусы A₁ и В₁, подобные и подобно расположенные соответственно конусам A и В. Конусы А₁ и В₁ пересекутся между собой (по теореме Мора) по двум плоским кривым - эллипсам I-I и II-Ii (на рис. 98 показаны проекции 1'₁ 1'₁ и 2'₁2'₁).

Определяем направление вспомогательного проектирования 2'₁р'₁ и плоскость проекций R, на которую эллипс II-II спроектируется в окружность.

Через конусы А и В проводим вспомогательную плоскость Q параллельно плоскости эллипса II-II. Эта плоскость рассечет конус А по эллипсу, большая ось которого MN, и конус В по эллипсу с большой осью KL. Проекцией этих эллипсов на вспомогательную плоскость R будут окружности а₁т₁b₁n₁ и c₁k₁d₁l₁; центры этих окружностей будут лежать на соответствующих проекциях осей конусов. Точки е и _f, в которых пересекаются эти окружности, являются вспомогательными проекциями двух точек, принадлежащих искомой кривой линии пересечения.

103

Рассекая конусы А и В рядом плоскостей Q₁, Q₂, Q₃ и т.д., параллельных плоскости Q, мы найдем требуемое количество точек, достаточное для точного построения кривой. Опорные точки могут быть найдены с помощью уже имеющихся окружностей и плоскостей Т и U, касательных к конусу А и B.

Для проведения плоскостей Т и U необходимо найти след прямой S₁S₂ на плоскости Q - q'. По q' определяем q₁.

Проекции следов T_Q и U_Q плоскостей, касательных к поверхности проекций конусов А и В на вспомогательную плоскость R (Т_R и Q_R), должны пройти через точку q₁. Положение точки q₁ и окружностей a₁m₁b₁n₁ и c₁k₁d₁l₁ определяют положение T_Q1 и U_Q1 (T_Q1 касается окружности а₁m₁b₁n₁ и проходит через точку q₁, U_Q1 касается окружности c₁k₁d₁l₁ и проходит через ту же точку q₁).

Очевидно, плоскости Т и U являются предельными, а точки III, IV, V, VI, найденные с их помощью - опорными (на рис. 98 указаны только их фронтальные проекции).

Вспомогательные секущие плоскости следует проводить так, чтобы проекции их следов на плоскость R находились между T_Q и U_Q.

Задача 2. Построить линию пересечения эллипсоида вращения с цилиндром вращения. Оси эллипсоида и цилиндра скрещиваются (рис. 99).

Как и в предыдущей задаче, строим пересекающиеся поверхности (цилиндрическую и эллиптическую), описанные около сферы. За диаметр сферы принимаем диаметр малой оси эллипсоида. Для сокращения количества графических построений за центр сферы принимаем центр эллипсоида. Такое положение центра позволяет обойтись без построения новой эллиптической поверхности.

Описываем около этой сферы цилиндрическую поверхность, подобно расположенную заданной цилиндрической поверхности.

На рис. 99 показаны только фронтальные проекции заданных и подобно расположенных поверхностей. На плоскости Н указаны только проекции осей эллипсоида и цилиндра.

Вспомогательные эллипсоид и цилиндр пересекаются по двум эллипсам I и II.

Направление проецирования, при котором эллипс I спроецируется на плоскость R₁, перпендикулярную этому направлению, очевидно, будет параллельным оси цилиндрической поверхности.

Рассекаем эллипсоид и цилиндр плоскостью Q, параллельной плоскости эллипса I. Эта плоскость рассечет эллипсоид по эллипсу, большая ось которого АВ проецируется без искажения в отрезок a'b', a цилиндр - по эллипсу, фронтальная проекция которого c'd' также равна натуральной величине большой оси.

104

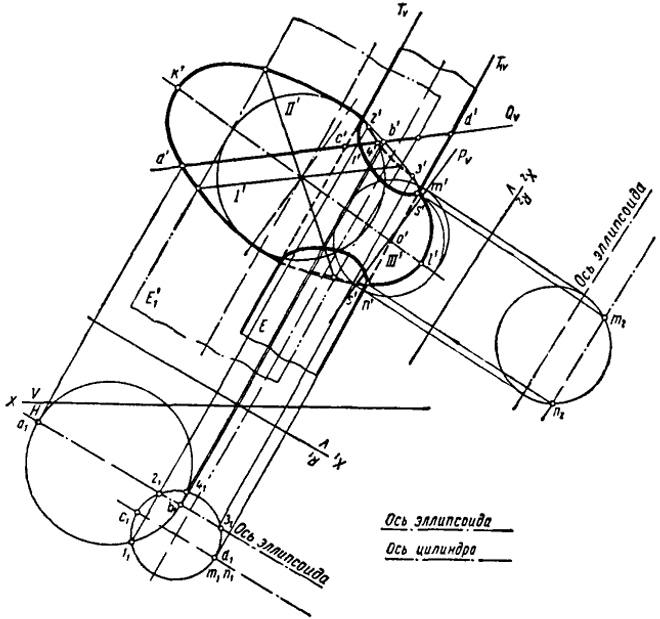
Рис. 99

Эллипсы АВ и CD подобны и расположены подобно эллипсу I, поэтому они спроецируются на плоскость R₁ в виде окружностей диаметрами а₁b₁ и c₁d₁. Точки пересечения этих окружностей 1₁ и 4₁ являются вспомогательными проекциями на плоскости R₁ двух точек, принадлежащих кривой пересечения.

Проводя ряд плоскостей Q₁, Q₂, Q₃ и т.д., параллельных плоскости эллипса I, можно получить достаточное количество точек, необходимых для построения кривой пересечения.

Опорные точки кривой, например точки, в которых пересекаются образующие цилиндра D и С с поверхностью эллипсоида (точки, определяющие границы видимости), могут быть определены с помощью фронтально-проецирующих плоскостей Т и Т₁, проведенных через эти образующие.

Очевидно, точки, в которых образующие D и С пересекут соответствующие эллипсы, полученные в сечении эллипсоида плоскостями Т

105

и Т₁, будут искомыми. Плоскость T рассекает эллипсоид по эллипсу III, малая ось которого может быть получена при помощи следующих построений.

Рассекаем эллипсоид плоскостью Р, проходящей через центр эллипса III, перпендикулярно оси эллипсоида KL. Отрезок s' - s' будет искомой величиной малой оси эллипса III.

Из центра эллипса III проводим окружность диаметром s' - s'. Касательная к этой окружности, проведенная через точки s' - s', укажет направление проецирования, при котором эллипс III спроецируется на плоскость R₂ (R₂ перпендикулярна полученному направлению проецирования) в окружность. Точки m₂ и n₂, в которых новая проекция оси цилиндра пересекает полученную окружность, являются искомыми вспомогательными проекциями точек встречи образующей цилиндра D с поверхностью эллипсоида.

С помощью обратных лучей определяем т' и n'. Аналогично находятся точки встречи образующей С с поверхностью эллипсоида. Проекции точек 2' и 3', лежащих на очерке эллипсоида, определяются непосредственно из чертежа.

Рассмотренные задачи были решены построением вспомогательных поверхностей подобно расположенных заданным. Затем определяли направление плоскостей Q₁ и Q₂, в которых лежат эллипсы-линии пересечения этих вспомогательных поверхностей.

Рассекая заданные поверхности плоскостями, параллельными Q₁ или Q₂, будем получать в сечении эллипсы, подобные и подобно расположенные эллипсам пересечения вспомогательных поверхностей.

Чтобы избежать построения эллипсов, было использовано вспомогательное параллельное проецирование на плоскость R, т.е. преобразование подобия мы применяли совестно с вспомогательным параллельным проецированием.

А.А. Кон предлагает использовать для решения задач на построение линий пересечения двух нелинейчатых поверхностей второго порядка центральное вспомогательное проецирование на параллельные плоскости S₁, S₂, S₃ и т.д.

При таком аппарате проецирования проекции геометрических фигур на плоскости S₁, S₂, S₃ окажутся подобными и подобно расположенными.

Помещенные ниже задачи показывают характер графических построений, которые должны быть выполнены для их решения с помощью центрального вспомогательного проецирования.

Задача 3. Построить линию пересечения шара с трехосным эллипсоидом (рис. 100).

106

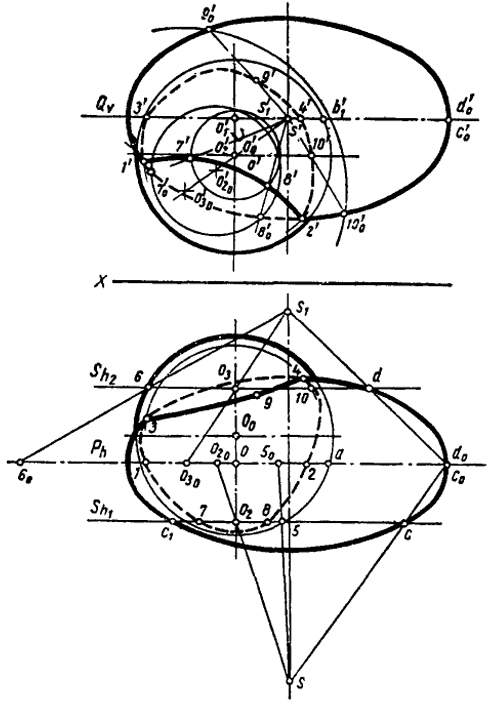
Рис. 100

Проводим плоскости Р и Q, проходящие через центр эллипсоида, параллельно фронтальной и горизонтальной плоскостям проекции. Эти плоскости рассекают эллипсоид по эллипсам, представляющим соответственно фронтальную и горизонтальную проекции очерка эллипсоида, а шар - по окружностям радиусов оа и о'₁b'₁.

Точки 1, 1'; 2, 2'; 3, 3'; 4, 4' определяются пересечением этих окружностей с проекциями очерка эллипсоида.

Для определения дополнительных точек линий пересечения поверхностей проводим ряд вспомогательных секущих плоскостей, параллельных V. Эти плоскости пересекут шар по окружностям, а эллипсоид по эллипсам.

107

Чтобы избежать построения эллипсов, воспользуемся центральным проецированием. Центр проекции S (он будет являться центром подобия сечений эллипсоида) выбирается так, чтобы вспомогательные проекции сечений эллипсоида совпали с очерком его фронтальной проекции. Положение центра S найдем с помощью прямой СС₀ в точке ее пересечения с осью эллипсоида, перпендикулярной к плоскости V.

Точки пересечения эллипса с₁с с окружностью o₂5 могут быть легко найдены, если спроецировать эллипс и окружность на плоскость Р из центра S.

Эллипс сечения спроецируется в эллипс - фронтальную проекцию эллипсоида. Для получения проекции окружности находим центральную проекцию ее центра о₂₀ о'₂₀ из о'₂₀ радиусом о₂₀ 5₀ проводим окружность.

Точки 7'₀ и 8'₀ пересечения этой окружности с фронтальной проекцией эллипсоида являются фронтальными вспомогательными проекциями точек пересечения. Искомые фронтальные проекции точек 7' и 8' находятся пересечением прямых 7'₀S' и 8'₀S' с фронтальной проекцией окружности o₂5, проведенной из центра о'₁. Таким путем можно найти любое количество точек линий пересечения.

На рис. 100 показано также построение точек 9 и 10 с помощью секущей плоскости S₂ и центра S₁. Одноименные проекции найденных точек соединяем плавной кривой.

Так может быть решена задача на определение линий пересечения поверхностей второго порядка при условии, что одна из них рассекается вспомогательными плоскостями по окружностям.

В тех случаях, когда ни одна из заданных поверхностей не может быть пересечена вспомогательной плоскостью по окружности, следует предварительно с помощью известного способа аффинного преобразования перевести одну из поверхностей в поверхность вращения.

Задача 4. Построить линию пересечения двух эллиптических параболоидов (рис. 101).

Так как невозможно получить окружность в сечении этих поверхностей плоскостью, то прежде чем приступить к решению задачи с помощью перспективно-аффинного преобразования, преобразуем параболоид А в параболоид вращения А₀. Построения аналогичны выполненным на рис. 85.

Если теперь преобразованные параболоиды А₀ и В₀ рассекать горизонтальными плоскостями Q, то линиями пересечения этой плоскости с параболоидом А₀ будет окружность, а с параболоидом B₀ - эллипс.

На оси параболоида В, перпендикулярной плоскости Н, выберем центр проецирования ss' так, чтобы вспомогательные горизонтальные

108

Рис. 101

проекции эллипса сечения совпали с горизонтальной проекцией очерка преобразованного параболоида В₀. Как и в предыдущей задаче, s' определяется пересечением е'b' с фронтальной осью параболоида В.

Далее определяем центральную проекцию на плоскость H центра окружности, по которой плоскость Q пересекает параболоид А. Из точки o₀₁ проводим окружность радиусом O'₀₁1'₀.

Точки пересечения центральных проекций сечений параболоидов плоскостью Q являются вспомогательными центральными проекциями точек 6, 7, 8, 9... искомой кривой линий пересечения. При помощи обратных лучей находим их ортогональные проекции. Одноименные проекции соединяем плавной кривой, выделив видимую часть от невидимой.

109