Зная закон преобразования плоских кривых, нетрудно выполнить преобразование поверхностей. Действительно, если представить, что плоская фигура, изображенная на рис. 93, вращается вокруг оси SB, то мы получим наглядное представление гомологического преобразования кривых поверхностей.
При таком вращении парабола опишет поверхность параболоида вращения, а окружность - шара. Если вместо параболы вращаться будет гипербола (рис. 94) или эллипс (рис. 90), то образуются соответственно
96
гиперболическая и эллиптическая поверхности, т.е. можно сделать вывод, что эллипсоид, параболоид и гиперболоид вращения могут гомологически преобразовываться в шар.
Очевидно, практическое выполнение таких преобразований дает возможность значительно упростить решения многих задач начертательной геометрии.
Проследим на конкретных примерах характер и последовательность построений, связанных с гомологическим преобразованием поверхностей. Так же, как при преобразовании плоских кривых, в данном случае должны быть соблюдены следующие условия:
- 1) центр гомологии должен лежать на оси вращения;
- 2) плоскость гомологии должна быть перпендикулярна оси вращения.
Преобразование параболоида вращения в шар. Графические построения, которые необходимо выполнить для преобразования параболоида вращения в шар, почти не отличаются от построений для преобразования параболы в окружность.
Построения отличаются лишь тем, что вместо двойной прямой MN (оси гомологии) появится двойная плоскость Р (плоскость гомологии). Кроме того, для получения более экономичного решения задачи оказывается целесообразным иметь шар с определенной, наперед заданной, величиной радиуса. Поэтому построения начинают с приведения проекций шара. Центр шара должен лежать на оси параболы. Величину радиуса шара выбираем из условия задачи (как правило, радиус следует выбирать по возможности большего размера, этим достигается большая точность последующих построений). В зависимости от величины радиуса и положения центра шара определяем центр и плоскость гомологии.
Рис. 95 дает представление о графическом решении задачи по преобразованию параболоида вращения в шар.
Решение выполнено в следующей последовательности:
- 1) из произвольной точки O0, о'0 оси параболы описываем окружности - проекции шара радиусом заданной величины;
- 2) определяем положение плоскости гомологии Р из условия, что окружность I, II, III, IV (проекции 1, 2, 3, 4 и 1', 2', 3', 4') по которой пересекаются параболоид с шаром, является двойной линией. Следовательно, эта окружность будет определять двойную плоскость преобразования;
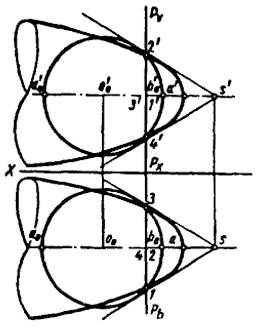
Рис. 95
97
- 3) центр гомологии S находим как вершину конической поверхности касательной к обеим поверхностям.
При помощи выполненных в вышеуказанной последовательности построений можно не только преобразовать параболоид вращения в шар нужных размеров, но и установить гомологическое соответствие между плоскостью Р, центром S и парой двойных точек АА0. Рассмотренный способ преобразования полностью сохраняется и в том случае, если преобразованию подвергается гиперболоид или эллипсоид вращения.
Преобразование эллипсоида вращения в шар было рассмотрено ранее (см. рис. 88) с помощью перспективно-аффинного преобразования.
Следует отметить, что в отличие от перспективно-аффинного преобразования, которое обеспечивает преобразование эллипсоида вращения в шар, диаметр которого равен диаметру окружности главного меридиана, гомология позволяет преобразовать эллипсоид в шар любого наперед заданного диаметра. Практическая целесообразность использования гомологических преобразований может быть показана на примере решения задачи по определению линии пересечения наклонного эллиптического конуса с поверхностью гиперболоида вращения (рис. 96).
Преобразование гиперболоида в шар. За плоскость гомологии Р примем горизонтальную плоскость проекции Н. Диаметр шара целесообразно взять равным диаметру горизонтальной проекции параболоида, а его центр - в точке пересечения оси параболы с плоскостью Н. Эти условия позволяют определить характер гомологических преобразований.
Вершина параболоида А преобразуется в точку A0 шара (на чертеже указаны только фронтальные проекции точек А и A0). Бесконечно удаленная вершина параболоида В преобразуется в точку В0.
Определить центр гомологии способом, изложенным выше, в данном случае не представляется возможным, так как точки касания прямой касательной к параболической и шаровой поверхностям отстоят друг от друга на бесконечно близком расстоянии. Поэтому для определения центра гомологии через вершину параболы А проводим плоскость R, параллельную плоскости проекции H.
При преобразовании пространства, обеспечивающего превращение гиперболы в шар, плоскость R преобразуется в R0, также параллельную H и проходящую через точку А0.
98
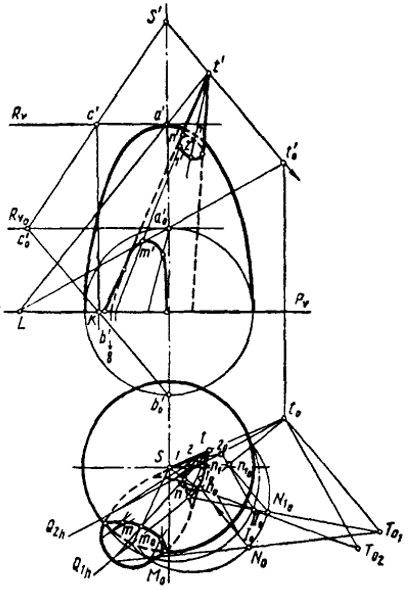
Рис. 96
Очевидно, любой преобразованной точке С0 плоскости R0 будет соответствовать точка С плоскости R.
Для нахождения пары соответствующих точек поступаем следующим образом. В произвольном месте плоскости R0 берем точку С0 и проводим прямую С0В0; соответствующая ей прямая ВС пройдет через двойную точку К. Так как точка В удалена в бесконечность, то ВС будет перпендикулярна к Pv.
Пересечение KB с плоскостью R определит исходное положение точки С. Зная положение двух пар соответствующих точек АА0 и СС0, находим центр гомологии S в точке пересечения прямых, проведенных через эти точки.
Теперь преобразование полностью установлено. Пользуясь им, находим положение преобразованной вершины конуса T0. Для этого через вершину конуса и параболы проводим прямую ТА до пересечения ее с плоскостью гомологии (точка L).
99
Через двойную точку L и A0 проводим прямую, соответствующую ТА. Пересечение LA0 с ST определяет положение преобразованной вершины конуса. Основание конуса лежит в плоскости гомологии, поэтому при преобразовании оно останется без изменения.
Благодаря выполненному преобразованию, сложная задача сведена к простейшей - нахождению точек встречи прямых (образующих конуса) с шаром. Эта задача решена с помощью секущих плоскостей. Точки встречи найдены в совмещенном положении, затем обратными лучами переносим их на образующие конуса и соединяем плавной кривой.
Чтобы не затруднять чтения чертежа, на рис. 96 показано построение только точек М, N, N1, I и II c помощью плоскостей Q1 и Q2.
100
