Перспективно-аффинное преобразование кривых второго порядка позволяет преобразовывать их в такие же кривые. Гипербола может быть преобразована в гиперболу, парабола - в параболу, эллипс - в эллипс, в частном случае, в окружность.
Преобразовать гиперболу или параболу в эллипс или окружность путем родственного преобразования не удастся. Поэтому упрощение в решении задач, в которых участвуют параболические или гиперболические поверхности, способом родственных преобразований мы достигаем лишь за счет преобразования их в поверхности вращения, т.е. путем преобразования эллиптических сечений в окружности. Очерки преобразованных поверхностей по-прежнему остаются параболическими или гиперболическими (см. рис. 86, 87).
Естественно, практический интерес представляет такое коллинеарное преобразование, которое дает возможность преобразовать одну кривую в другую, в частности, параболу и гиперболу в окружность. Если нам удастся выполнить такие преобразования, то мы сможем преобразовать параболические и гиперболические поверхности в шаровые. Возможность такого преобразования открывается с использованием свойств гомологии.
Рассмотрим гомологическое преобразование окружности в эллипс, параболу и гиперболу.
Рис. 89 дает наглядное представление о гомологическом преобразовании окружности в пространстве. Эти преобразования соответствуют сечениям конической поверхности, образованной лучами преобразования, плоскостями P0, P01, P02. Если представить, что центр гомологии S лежит в плоскости окружности, тогда преобразующие лучи будут находиться в плоскости Р, в ней же будут лежать и преобразованные точки кривой, т.е. будет иметь место гомологическое преобразование в совмещенных полях. Остановимся на случае, когда луч преобразования, проходящий через S и центр окружности, перпендикулярен двойной плоскости.
91
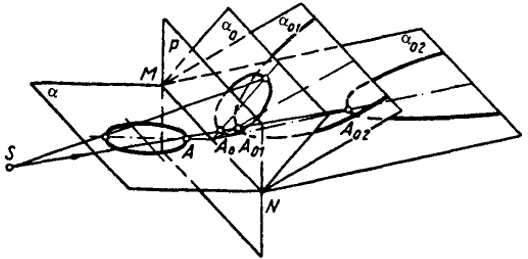
Рис. 89
В зависимости от характера заданного преобразования, положения точек A0, А01, А02, при неизменных S и Р, окружность преобразуется в эллипс, параболу или гиперболу (рис. 90-92).
Эллипс с проективной точки зрения можно рассматривать как кривую, полученную в результате преобразования окружности. При этом пространство, в котором находилась окружность, должно быть преобразовано в новое пространство так, чтобы прямые первого пространства, преобразующиеся в бесконечно удаленные прямые второго пространства, не имели общих точек с окружностью. Иными словами, окружность преобразуется в эллипс, если гомологическим преобразованием преобразуется в бесконечно удаленную прямую прямая, не имеющая общих точек с заданной окружностью.
Таких прямых может быть бесчисленное множество. К ним относятся все прямые, параллельные плоскости Р, не пересекающие окружности и не касающиеся ее. Поэтому окружность гомологически может быть преобразована в бесчисленное множество эллипсов.
На рис. 90 показаны различные варианты эллипсов, в которые преобразуется окружность. Чтобы построить эллипс, соответствующий окружности, необходимо найти ряд точек эллипса, соответствующих точкам окружности. В качестве таких точек целесообразнее (в смысле простоты построений) взять точки А и В концов диаметра окружности и С и С1 точки касания преобразующего луча к окружности.
Преобразованное положение этих точек A0, B0, С0 и С10 определяем с помощью прямых АС и СВ. Через двойные точки этих прямых К и L проводим соответствующие им прямые. Прямую КА0 проводим произвольно. Она пересекает SC в точке С0, a SA в A0. Через С0 и L проводим прямую, пересекающую SA0 в точке B0. Имея точки A0, С0, В0, С10, легко построить эллипс (С10 расположена симметрично С0 относительно SA0). Для более точного построения эллипса можно определить любое количество точек.
92
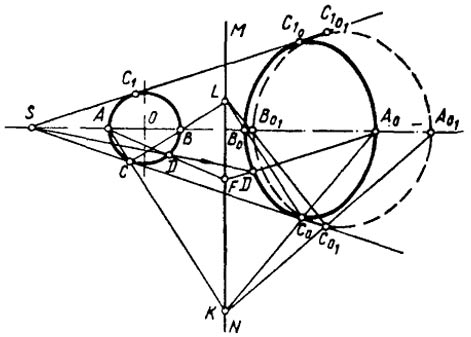
Рис. 90
На рис. 90 показано построение D0 произвольной точки D окружности.
В зависимости от направления прямой КА0, соответствующей АК, мы будем получать различное положение точек A0, A01, A02 и т.д., а следовательно, и новое положение других точек эллипса В0, B01, B02…С0, С01, С02 и т.д. Эти точки определяют форму и положения бесчисленного множества эллипсов.
На рис. 90 в качестве примера, кроме эллипса А0В0С0С10, показан эллипс A01B01C01C10, большая ось которого А01В01.
Характер гомологических преобразований, при котором окружность преобразовывается в параболу, может быть установлен, исходя из свойств параболы. Известно, что парабола - это кривая второго порядка, касающаяся бесконечно удаленной прямой. Поэтому окружность преобразуется в параболу, если гомологическим преобразованием прямая, касательная к окружности, преобразуется в бесконечно удаленную прямую.
Очевидно, касательными к окружности, которые могут быть преобразованы в бесконечно удаленные прямые, будут две прямые, параллельные плоскости Р и проходящие через точки А и В. Следовательно, окружность может быть преобразована в две параболы; одну при преобразовании точки А в бесконечно удаленную точку A0; другую при таком же преобразовании точки В.
На рис. 91 показано преобразование окружности в параболы. Построения выполнены только для нахождения точек С0, В0 правой параболы и C01, A01 левой параболы, а также произвольной точки D0 правой параболы.
93
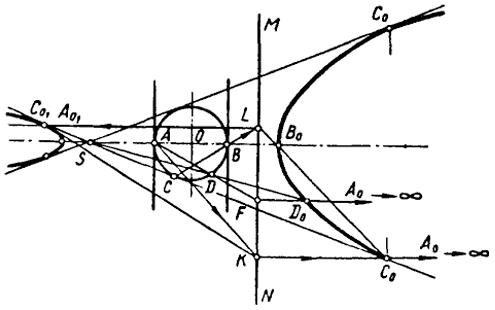
Рис. 91
Правило преобразования окружности в гиперболу может быть сформулировано: окружность преобразуется в гиперболу, если гомологическим преобразованием прямая, пересекающая окружность, преобразуется в бесконечно удаленную прямую. Это правило получено нами из свойств гиперболы, которая, как известно, пересекает бесконечно удаленную прямую в двух точках.
Уже говорилось, что прямая может быть преобразована в бесконечно удаленную прямую, если она параллельна плоскости гомологии. Очевидно, можно провести бесчисленное множество прямых, параллельных MN и пересекающих окружность в двух точках. Поэтому заданная окружность может быть преобразована в бесчисленное множество гипербол.
На рис. 92 показано построение только ветви гиперболы, соответствующей дуге DBD1; вершина гиперболы точка В0 может быть найдена с помощью преобразовывающего луча SD и прямой LD0→∞ соответствующей
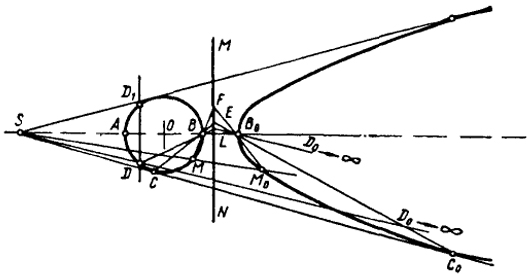
Рис. 92
94
прямой DL, проходящей через точки D и В. LD0→∞ проводится параллельно SD (это будет соответствовать удалению точки DO в бесконечность). Пересечение LD0→∞ с прямой SB определяет точку В0.
Зная положение В0, легко построить любое количество точек ветви гиперболы.
На чертеже показано построение только точек С0 и М0. Нахождение этих точек выполнено обычными построениями, характерными для определения точек, соответствующих заданным при данном гомологическом преобразовании.
Приведенные гомологические преобразования кривых второго порядка можно рассматривать так же, как преобразование эллипса, параболы и гиперболы в окружность, что имеет гораздо большее практическое применение при решении задач. Преобразование эллипса в окружность целесообразно осуществлять путем родственных преобразований (см. рис. 82).
Покажем способ гомологического преобразования параболы и гиперболы в окружность.
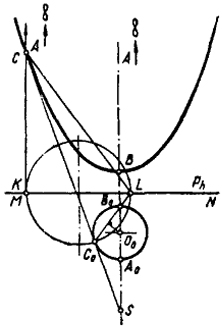
Преобразование параболы в окружность. На рис. 93 показаны построения, которые необходимо выполнить для преобразования параболы в окружность.
При заданных плоскости Р и точке S гомологическое преобразование будет полностью определено, если мы укажем еще пару соответствующих точек. Эти точки могут быть найдены из следующих соображений. Мы знаем, что при любом коллинеарном преобразовании касательная k кривой в заданном положении останется касательной к кривой и после преобразования (касание является инвариантом коллинеарного преобразования). При этом точки касания будут взаимно соответствующими точками.
На основании сказанного следует, что касательная к параболе SC, проведенная через центр гомологии, преобразуется в касательную к окружности SC0.
Для нахождения точки касания С0 через С проводим две хорды параболы, соединяющие концы ее диаметра, СВ и СА. Так как точка А удалена в бесконечность, то СА будет параллельна ВА. Отрезок, определяемый двойными точками К и L, принимаем за диаметр вспомогательной окружности. Эта окружность пересекает прямую SC в точке C0. Через C0 проводим хорду C0L, соответствующую хорде CL. Пересечение С0L с SB определяет положение точки В0.
Имея точки С0 и В0, принадлежащие окружности, и зная, что центр ее находится на прямой SB0, легко построить окружность, в которую преобразовывается парабола.
95
 |
 |
| Рис. 93 |
Рис. 94 |
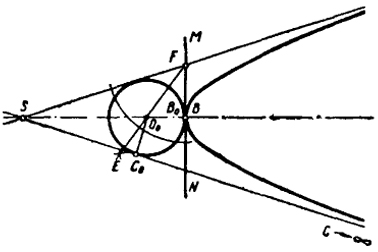
Преобразование гиперболы в окружность. Для того чтобы преобразовать гиперболу в окружность (рис. 94), целесообразно центр гомологии поместить в центр гиперболы (точка пересечения асимптот). В этом случае асимптоты будут являться касательными лучами преобразования.
Чтобы упростить дальнейшие построения, прямую MN лучше взять касательной к вершине гиперболы в точке В. Тогда точка В0 окружности и соответствующая ей вершина гиперболы В совпадут. Центр окружности должен лежать на прямой BS, а окружность касаться асимптоты.
Поэтому для нахождения центра окружности О0 достаточно провести биссектрису FE угла SFB до ее пересечения с SB. Из O0 радиусом О0В0 проводим окружность, в которую преобразовывается гипербола.
96
