Ранее отмечалось, что при коллинеарном преобразовании точки первого пространства преобразуются в точки второго пространства, прямые преобразуются в прямые, плоскости - в плоскости.
Поэтому легко убедиться, что при перспективно-аффинном преобразовании призме будет соответствовать призма; действительно каждой паре пересекающихся плоскостей заданной фигуры должна соответствовать также пара пересекающихся плоскостей; при этом линия их пересечения будет родственной линии пересечения заданных плоскостей. Следовательно, у родственной (преобразованной) фигуры будет столько же граней и ребер, сколько их было у оригинала.
Если учесть, что при перспективно-аффинном преобразовании параллельным прямым и плоскостям будут соответствовать также параллельные прямые и плоскости, родственные заданным, то станет очевидным, что призма преобразуется в призму. Нетрудно показать, что пирамида родственно может быть преобразована только в пирамиду.
Линейчатые поверхности второго порядка после преобразования остаются линейчатыми. Например, преобразование конуса или цилиндра сводится к нахождению линий, родственных их криволинейным направляющим и прямолинейным образующим, которые после преобразования остаются соответственно кривыми и прямыми. Поэтому конус и цилиндр при родственном преобразовании остаются конусом и цилиндром.
Рассуждая аналогично, можно показать, что нелинейчатые поверхности второго порядка могут быть родственно преобразованы только в однотипные поверхности: эллипсоиду будет соответствовать эллипсоид; в частном случае - шар; эллиптическому параболоиду -
83
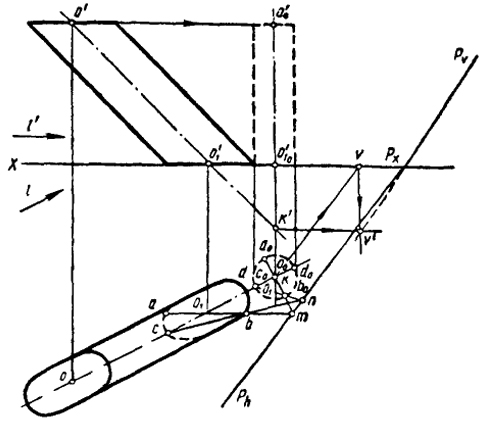
Рис. 83
эллиптический параболоид, в частности - параболоид вращения и т.д.
Мы уже отмечали, что метод пространственных преобразований предусматривает преобразование заданной фигуры в другую, вид и свойства которой позволяют облегчить решение поставленной задачи. Очень часто приходится иметь дело с задачами, в которых требуется определить форму сечения поверхности второго порядка плоскостью или характер линии пересечения двух тел, ограниченных криволинейными поверхностями второго порядка.
Такие задачи решаются просто, если поверхности будут проецирующими (в случае линейчатых поверхностей) или поверхностями вращения (для нелинейчатых поверхностей). Поэтому рассмотрение вопроса использования перспективно-аффинного преобразования для решения задач начнем с построения проецирующих поверхностей и поверхностей вращения, родственных заданным.
Пример 1. Преобразовать наклонный эллиптический цилиндр в прямой круговой цилиндр (рис. 83).
Для того чтобы ось цилиндра стала перпендикулярной к плоскости Н, горизонтальные проекции двух ее точек должны совпасть. Это может быть достигнуто, если горизонтальную проекцию направления преобразования l примем параллельно oo1.
Чтобы окружность преобразованного основания лежала в плоскости Н, фронтальную проекцию l' выбираем параллельной оси X.
84
Дальнейшие построения выполняются в следующем порядке: в произвольном месте прямой оо1 берем точку o0, центр преобразованной окружности; через горизонтальные проекции крайних образующих цилиндра проводим горизонтальные проекции линий связи, они будут касаться окружности в точках а0 и b0 (отрезок а0b0 перпендикулярен оо1). Отрезок а0b0 определит величину диаметра окружности.
Имея горизонтальную проекцию преобразованного цилиндра, не составляет труда построить его фронтальную проекцию.
Построив проекции преобразованного цилиндра родственного заданному, определяем плоскость родства. Для нахождения горизонтального следа этой плоскости воспользуемся точками а, b, с и родственными им точками a0, b0, c0.
Через аb и сb проводим прямые, которые пересекаются с соответствующими им прямыми a0b0 и c0b0 в двойных точках т и п. Через т и п пройдет след Ph. Фронтальный след плоскости Pv может быть найден с помощью двойной точки k, принадлежащей оси цилиндра. Проведя через k горизонталь, определяем ее фронтальный след. Pv пройдет через точку v'.
В данном примере определение положения плоскости родства является лишней операцией. Но мы его приводим, так как произведенное преобразование не является самоцелью, а необходимо для решения задачи, в которой, кроме цилиндра, участвуют другие геометрические фигуры. Положение следов Ph и Pv позволяет выполнить родственное преобразование этих фигур.
Приведенный пример дает нам возможность выяснить одну важную особенность метода пространственных преобразований, заключающуюся в том, что мы можем заранее задать определенные свойства преобразованной фигуры, а затем определить положение плоскости родства.
Пример 2. Преобразовать эллиптический гиперболоид в гиперболоид вращения.
Решим эту задачу при различном положении плоскости родства.
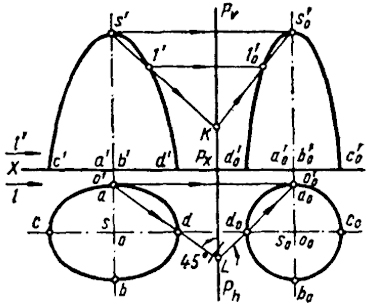
1-й вариант (рис. 84). Плоскость родства принимаем параллельной профильной плоскости проекции; направление родства перпендикулярно ей. Чтобы установить родственное соответствие, необходимо задаться еще одной парой родственных точек.
При выборе положения этих точек следует исходить из условия, что преобразованная поверхность оказалась поверхностью вращения. Для того чтобы эллиптический гиперболоид преобразовался в гиперболоид вращения, нужно, чтобы эллипсы нормальных сечений преобразовывались в окружность. Построения аналогичны выполненным на рис. 82.
85
 |
 |
| Рис. 84 |
Рис. 85 |
Для построения фронтальной проекции гиперболоида вращения можно воспользоваться наличием плоского родственного соответствия между преобразованным и заданным гиперболическим контуром. В качестве примера показано построение точки 1'0, родственной точке 1'.
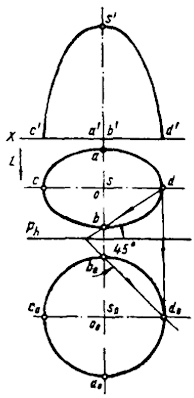
2-й вариант. Преобразования, выполненные на рис. 84, потребовали построения двух (горизонтальной и фронтальной) проекций родственной фигуры. Этого можно избежать и ограничиться вычерчиванием только одной родственной проекции, если за плоскость родства взять плоскость, параллельную фронтальной плоскости проекции.
Направление преобразования выбираем перпендикулярным плоскости родства, а диаметр окружности сечения преобразованного гиперболоида вращения принимаем равным большому диаметру эллипса сечения, параллельного плоскости V.
На рис. 85 выполнены построения, которые необходимы для нахождения горизонтальной проекции гиперболоида вращения соответствующего заданному при установленном выше характере родства.
Как и в первом варианте, через концы двух диаметров d и b проводим прямую и строим родственную ей прямую d0b0, при этом угол между d0b0 и Ph равен 45°. Это обеспечивает преобразование эллипса в окружность диаметром, равным большему диаметру эллипса.
86
При таких условиях фронтальная проекция преобразованного гиперболоида совпадает с фронтальной проекцией заданного эллиптического гиперболоида.
В результате выбора плоскости родства параллельно V отпадает необходимость строить дополнительную фронтальную проекцию родственной фигуры.
Преобразование других нелинейчатых поверхностей в поверхности вращения выполняется аналогично только что разобранному примеру.
Родственное преобразование пространства с расположенными в нем различными фигурами позволяет значительно проще, чем любым из ранее рассмотренных методов, решать некоторые сложные задачи начертательной геометрии.
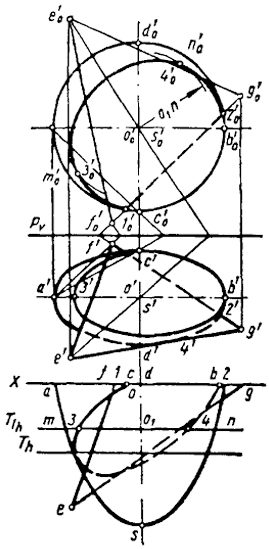
Задача 1. Даны эллиптический параболоид и трехгранная призма; требуется определить линии пересечения граней призмы с поверхностью параболоида (рис. 86). Очевидно, решение этой задачи способом секущих плоскостей потребует построения большого количества вспомогательных эллипсов. Вычерчивание эллипсов можно заменить проведением окружностей, если с помощью родственного соответствия преобразовать эллиптический параболоид в параболоид вращения.
Ход решения задачи будет следующим: проводим горизонтальный след плоскости родства Рh, параллельно оси X. Находим точку d0, родственную точке d, на прямой d0b0, родственной прямой ab, причем d0b0 проводим под углом 45° к Рh,. Это обеспечит преобразование эллипса в окружность, а эллиптическую поверхность в поверхность вращения. Зная Рh и dd0, легко определить горизонтальную проекцию призмы k0m0l0, соответствующую данной при заданном условии родства. Выполненные преобразования позволяют просто решить поставленную задачу с помощью вспомогательных секущих плоскостей.
Фронтальная проекция точки 1 пересечения ребра призмы К с поверхностью параболоида лежит на фронтальной проекции очерка и может быть найдена непосредственно. Также непосредственно определяется фронтальная проекция точки 4.
Точки 2 и 3, в которых ребра М и L призмы пересекают поверхность параболоида, находятся с помощью окружностей, по которым плоскости Т1 и T2 пересекают преобразованную поверхность параболоида. Радиусы окружностей соответственно равны o0m0 и о0l0. Построение начинаем с проведения дуг через точки т0 и l0. Из точек пересечения этих дуг с горизонтальным диаметром родственного параболоида восставляем перпендикуляры до пересечения их с фронтальной проекцией очерка гиперболоида. Через полученные точки пройдут
87
 |
 |
| Рис. 86 |
Рис. 87 |
следы вспомогательных секущих плоскостей Т1 и Т2, на которых будут лежать фронтальные проекции точек 2 и 3. Также находим точки 5, 6.
Чтобы не затруднять чтения чертежа, мы показываем построение только точек 5 и 6, которые являются одновременно низшими точками линий пересечения граней К12М и K13L с параболической поверхностью.
Определение сечения нелинейчатой поверхности второго порядка плоскостью общего положения не вносит каких-либо конструктивных изменений в ход решения задачи. Чтобы убедиться в этом, решим следующую задачу.
Задача 2. Даны фигура Φ, ограниченная поверхностью эллиптического параболоида, основание фигуры совпадает с фронтальной плоскостью проекции и пластина EFG, определяющая плоскость общего положения Q. Найти сечение фигуры плоскостью (рис. 87).
88
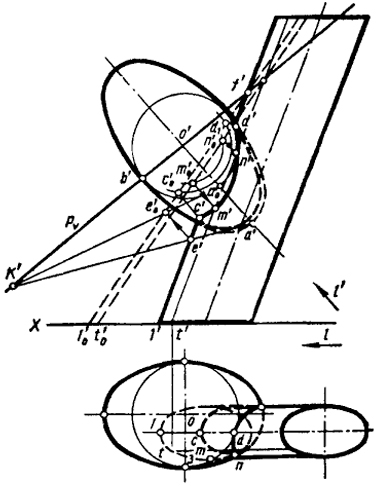
Рис. 88
Преобразуем фигуру Φ в родственную фигуру Φ01, а плоскость EFG в родственную ей плоскость E0F0G0. Для этого задаем родственное соответствие так же, как в предыдущей задаче, с той лишь разницей, что плоскость родства принимаем параллельно Н.
Выполнив преобразование, мы можем воспользоваться для решения задачи способом секущих плоскостей. На произвольном расстоянии от плоскости V проводим секущую плоскость Т1; эта плоскость пересекает плоскость пластинки по фронтали MN, а поверхность параболоида по эллипсу, которому на преобразованной поверхности соответствует окружность радиуса о1т. Пересечение этой окружности с преобразованной фронталью M0N0 определит точки 30 и 40, родственные точкам 3 и 4 заданной фигуры.
Проведя ряд секущих плоскостей, можно легко найти необходимое количество точек, по которым строится кривая линия пересечения.
Задача 3. Найти линию пересечения наклонного эллиптического цилиндра с эллипсоидом вращения. Ось вращения эллипсоида и ось цилиндра параллельны плоскости V и не пересекаются (рис. 88).
89
В предыдущих задачах плоскость родства мы принимали параллельной плоскости проекций. В данной задаче плоскость родства Р целесообразно взять перпендикулярной оси вращения эллипсоида, а направление преобразования L параллельно этой оси. В этом случае оказывается возможным преобразовать эллипсоид вращения в шар, если точку А преобразовать в А0 так, чтобы а'0о' = b'о'(ВО).
Цилиндр, как уже отмечалось, преобразуется в цилиндр. Фронтальная проекция преобразованного цилиндра (построения горизонтальной проекции для решения задачи не требуется) может быть найдена путем следующих построений.
Преобразуем образующую цилиндра 1, используя для этого точки а' и а'0; через а' проводим произвольную прямую а'k' (К-двойная точка этой прямой), строим родственную ей прямую а'0k'.
Точка е' принадлежит образующей цилиндра 1, следовательно, в преобразованном положении образующая 1'0 пройдет через е'0. В качестве другой точки, определяющей положение 1'0, воспользуемся двойной точкой f'. Фронтальные проекции остальных образующих будут параллельны 1'0 и пройдут через соответствующие двойные точки (точки их пересечения с Pv)- Теперь нам остается определить точки встречи этих образующих с поверхностью шара и обратными лучами возвратить их на образующие заданного цилиндра. На рис. 88 такие построения показаны для точек М и N, в которых произвольная образующая цилиндра Т пересекает поверхность эллипсоида.
Рассмотренная задача показывает, что, используя родственное преобразование пространства, мы можем легко решать задачи по определению линий пересечения тел, ограниченных нелинейчатыми поверхностями второго порядка с призмами, пирамидами или цилиндрами, произвольно расположенными в пространстве.
Решение задач, в которых участвуют две фигуры, ограниченные нелинейчатыми поверхностями второго порядка, способом, основанным на родственном преобразовании пространства, не дает существенного упрощения.
Это объясняется тем, что родственно преобразовывая пространство, мы можем добиться, чтобы одна из поверхностей преобразовалась в поверхность вращения; при этом вторая поверхность преобразуется вновь в поверхность общего вида. Избежать вычерчивания эллипсов нам не удастся, единственное, чего мы можем достигнуть, это вдвое сократить их количество.
Одновременное родственное преобразование двух нелинейчатых поверхностей второго порядка в поверхности вращения может быть осуществлено только в том частном случае, когда, во-первых, оси обеих
90
поверхностей параллельны друг другу и, во-вторых, эллипсы нормальных сечений обеих поверхностей подобны и подобно расположены.
Такую задачу мы находим у И.С. Джапаридзе [9].
91
1
Φ0 - фигура, ограниченная поверхностью вращения.
