При перспективно-аффинном преобразовании пространства кривым второго порядка родственно будут соответствовать только однотипные кривые того же порядка.
Пусть дана окружность радиуса ОА, лежащая в плоскости Р, и задано перспективно-аффинное соответствие плоскостью родства Р1 и положением точки А0 родственной А (рис. 79). Двойная прямая (ось родства)
79

Рис. 79
MN и точка A0 определяют плоскость Р0, родственную заданной плоскости. Кривая, родственная окружности ОА, будет лежать в плоскости P0. При этом точка A0 является собственной точкой пересечения преобразующего луча (линии связи) с плоскостью Р0 и будет принадлежать соответствующей кривой.
Из проективной геометрии известно, что если один из лучей параллельного пучка пересекает плоскость в ее собственной точке, то и все остальные лучи будут пересекать эту плоскость в собственных точках.
Возвращаясь к нашему примеру, можно сделать вывод, что окружность, как кривая, не имеющая бесконечно удаленных (несобственных) точек, после перспективно-аффинного преобразования также не будет их иметь.
Иными словами, окружности (или эллипсу) родственно соответствует окружность или эллипс. Что касается параболы, то, очевидно, она, как кривая, имеющая несобственные точки, родственно может быть преобразована только в кривую, также имеющую несобственные точки, т.е. в параболу. Гипербола может быть преобразована в гиперболу.
Два последних случая, с точки зрения преобразования ортогональных проекций, не имеют никакого смысла. Они не вносят никаких конструктивных изменений в решение задач начертательной геометрии, а следовательно, не могут ни упростить, ни уточнить этого решения.
Поэтому мы остановимся только на случае родственного преобразования окружности (эллипса).
Из рис. 79 следует, что в зависимости от задания родственного соответствия (положения точки A0 на линии связи, при неизменном положении плоскости Р1) исходная окружность может быть преобразована
80

Рис. 80
в бесчисленное множество эллипсов. Различному положению преобразованной точки A0, A01, A02 соответствуют плоскости P0, P01, Р02 с расположенными в них родственными эллипсами.
Мы знаем, что аффинное преобразование сохраняет пропорциональность деления отрезка в данном отношении, поэтому центр окружности, как точка, делящая все диаметры пополам, преобразуется в центр эллипса, а взаимно сопряженные диаметры окружности - соответственно в сопряженные диаметры эллипса.
В связи с этим для родственного преобразования окружности (или эллипса) целесообразно воспользоваться двумя ее диаметрами.
Рассмотрим общий случай родственного преобразования окружности.
На рис. 80 проекции окружности заданы двумя сопряженными диаметрами: АВ - совпадающего с направлением горизонтали плоскости и CD - параллельного линии наибольшего ската этой плоскости. Аффинное соответствие определено плоскостью родства Р и преобразованным положением центра окружности O0.
Преобразованное положение проекций сопряженных диаметров эллипса a0b0c0d0, родственных диаметрам окружности, определяем с помощью двойной прямой MN, являющейся линией пересечения плоскости родства Р с плоскостью окружности.
Точки а0 и b0 найдены пересечением прямых связи, проходящих через точки а и b, с прямой ko0, родственной прямой ab. Точки с0 и d0 находятся на прямой lo0, родственной cd.
81
 |
 |
| Рис. 81 |
Рис. 82 |
Имея горизонтальные проекции a0b0, c0d0 и зная направление фронтальных проекций прямых связи (о'о'0), легко определяем фронтальные проекции a'0b'0 и c'0d'0. По двумя проекциям сопряженных диаметров эллипса строим его проекции.
На рис. 81 разобран частный случай, когда окружность лежит в горизонтальной плоскости проекций Н. Аффинное соответствие определяется плоскостью Р, параллельной фронтальной плоскости проекции, и преобразованным положением A0 точки А (аа0 перпендикулярен оси родства Ph).
Для определения положения точки d0, родственной точке d, проводим прямую ad до пересечения с осью родства в точке k. Зная точку k, находим прямую ka0, родственную ka. Точка d0 определится пересечением прямых ka0 и dd0 (dd0 ‖ аа0).
Диаметр окружности dc, параллельной оси родства, преобразуется в родственный диаметр эллипса d0c0, также параллельный оси родства. Поэтому, имея d0, легко определяем O0 и C0, а также и b0 (C0O0 = d0o0, a b0о0 = а0о0). Положение точек о0, с0 и b0 могло быть определено и самостоятельно. На рис. 81 показано определение b0 с помощью прямой dl и родственной ей прямой d0l.
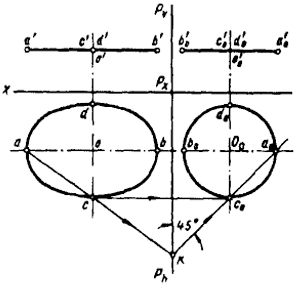
Практический смысл, очевидно, будет иметь не преобразование окружности в эллипс, а наоборот.
На рис. 82 показаны построения, которые необходимо выполнить, чтобы преобразовать эллипс, лежащий в плоскости, параллельной Н, в окружность.
Очевидно, такое преобразование может быть осуществлено только при определенном задании плоскости родства и пары родственных
82
точек, причем положение родственных точек будет зависеть от того, какой будет выбрана плоскость родства Р.
Для упрощения построений плоскость Р принимаем параллельной плоскости W, а направление линий связи перпендикулярно ей.
Через точки a и с проводим прямую, пересекающую Рh, в точке k.
Для того чтобы отрезки а0а0 и o0c0 были равны, необходимо, чтобы точки a0 и с0, родственные точкам а и с, лежали на прямой, составляющей с Ph, угол в 45°.
Через k проводим такую прямую, на ней определяем a0 и с0. Имея с0, легко найти центр окружности о0, родственной заданному эллипсу.
83
