ВВЕДЕНИЕ

В начертательной геометрии задачи решаются графически.

При этом количество и характер геометрических построений определяются не только сложностью задачи, но и в значительной степени зависят от взаимного расположения проектируемой фигуры и плоскостей проекций.

Произвольное по отношению к плоскостям проекций расположение фигуры при ортогональном проецировании на взаимно перпендикулярные плоскости дает проекции, которыми неудобно пользоваться для решения той или иной конкретной задачи.

Действительно, ортогональные проекции abc и a'b'c' треугольника ABC (рис. 1, а) не дают возможности непосредственно судить о длине его сторон, величине углов при вершинах и других геометрических характеристиках треугольника. Между тем, если бы плоскость треугольника оказалась параллельной какой-либо плоскости проекции (в нашем случае параллельной плоскости V, рис. 1, б), то при том же (ортогональном) способе проецирования он будет проецироваться на плоскость V в натуральную величину. Вид фронтальной проекции дает нам возможность непосредственно ответить на вопросы, получение которых на рис. 1, а связано с необходимостью дополнительных построений.

Можно было бы привести много примеров, показывающих, какое существенное влияние оказывает взаимное расположение объекта проецирования и плоскостей проекции на простоту решения метрических задач.

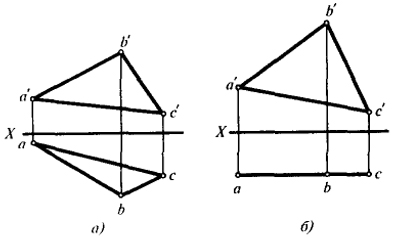
Рис. 1

4

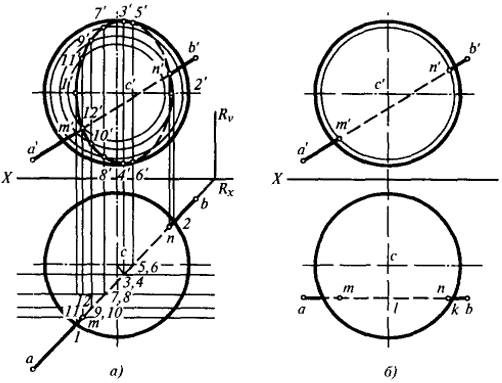
Рис. 2

Известно, что удобство решения позиционных задач также зависит от характера расположения объекта проецирования по отношению к плоскостям проекций.

В качестве примера, подтверждающего это положение, рассмотрим задачу по определению точек пересечения прямой с поверхностью сферы (рис. 2, а, б).

На рис. 2, б эта задача может быть решена при минимальном количестве графических построений. Задача сводится к определению точек т' и п' пересечения а'b' с окружностью радиуса r = lk, проведенного из центра в точке с'

На рис. 2, а для получения ответа приходится делать большое количество построений (на рис. 2, а указана только часть необходимых построений). Следовательно, и здесь условия взаимного расположения проецируемого объекта и плоскостей проекций значительно влияют на характер и количество графических построений.

Обычно в учебниках и пособиях по начертательной геометрии пишут, что объект проецирования может занимать "выгодное" или "невыгодное" ("удобное" или "неудобное", "рациональное" или "нерациональное" и т.п.) положение. При этом определение "выгодное" или "невыгодное" относится к изображаемому объекту. Это утверждение справедливо при ортогональном способе проецирования на взаимно перпендикулярные плоскости. В этом случае вид и положение проекции зависят от положения объекта проецирования по отношению к плоскостям проекций.

5

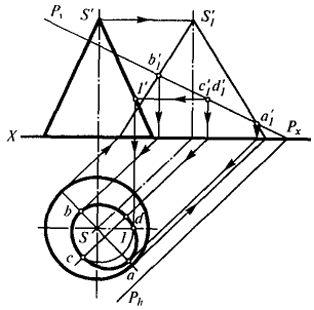
Рис. 3

Ниже будут рассмотрены способы преобразования ортогональных проекций, при этом в некоторых используются косоугольное и центральное проецирование, а также различные способы преобразования проекций пространственных образов, включая коллинеарные и топологические.

Очевидно, во всех перечисленных случаях "выгодное" или "невыгодное" расположение фигуры теряет свой смысл, так как расположение фигуры, определяющее невыгодный вид ее проекций при ортогональном проецировании, может дать чрезвычайно выгодный вид проекции при другом направлении или способе проецирования.

На рис. 3 показаны ортогональные проекции прямого кругового конуса и секущей плоскости Р. Ясно, что для определения сечения при ортогональном проецировании положение плоскости Р является невыгодным; в то же время, если спроецировать плоскость Р и конус S на плоскость V в направлении горизонтали плоскости Р, можно получить новую фронтальную проекцию, весьма удобную для решения задачи¹. Поэтому в дальнейшем мы будем говорить не о "выгодном" или "невыгодном" положении проецируемой фигуры, а о ее проекциях, считая их удобными в том случае, если они позволяют ясно представить форму и размеры геометрической фигуры и упростить решение поставленной задачи.

6

Возвращаясь к рис. 1-3, видим, что задачи решаются весьма просто в случае удобного вида проекции и значительно осложняются при неудобном виде проекций заданных геометрических образов.

В связи с этим, естественно, возникает вопрос: какими путями можно получить проекции удобного для решен конкретной задачи вида?

Ниже будут показаны различные способы получения проекций, упрощающих решение задач начертательной геометрии, посредством заданных - неудобных ортогональных проекций.

Преобразование ортогональных проекций должно сводиться к получению нового вида проекций, позволяющего решить задачу минимальными графическими средствами.

Возможность получения новых проекций, которые в дальнейшем будем называть вспомогательными, была показана еще Г. Монжем [21].

При решении ряда задач Монж широко пользовался методом вращения для определения истинной длины отрезка прямой и вида плоской фигуры¹ .

В некоторых задачах для этой цели он применял замену одной плоскости проекции и указал на возможность получения новых ортогональных проекций на две пересекающиеся под произвольным углом плоскости.

Основоположник начертательной геометрии в России Я.А. Севастьянов [26] писал о целесообразности применения, в ряде случаев, косоугольного и центрального проецирования: "Иногда употребление проекций наклонной или косвенной и перспективной в некоторых случаях облегчает решения, которые имеют место, посредством проекций перпендикулярных..."

В последующие годы способы вращения и замены плоскостей проекций были достаточно хорошо разработаны и стали широко применяться при решении различных задач.

Наиболее полное современное изложение этих способов имеется у В.И. Курдюмова, автора большого количества фундаментальных трудов по начертательной геометрии [17]. В.И. Курдюмов показал теоретическую возможность и практическую целесообразность пользоваться при решении некоторых задач сочетанием двух способов (вращения и замены плоскостей проекции). Такие преобразования он назвал сложными перемещениями.

7

В тридцатых годах XX в. С.М. Колотов изложил основные принципы способа косоугольного и центрального проецирования на специально выбранную плоскость, получившего названия способа вспомогательного проецирования [15].

В разработке и дальнейшем усовершенствовании способа вспомогательного проецирования принимала участие большая группа российских и украинских ученых, которыми был разработан ряд самостоятельных способов построения вспомогательных проекций, например работы P.M. Минина, Р.С. Бриллинга, В.П. Левина, Л.С. Скрипова, М.М. Юдицкого, С.В. Михайлова, Н.Т. Чувикова и др.

Авторы А.И. Руубель, А.И. Каченюк, A.M. Тевлин, А.Л. Подгорный, Н.К. Грушинская и другие занимались вопросами получения вспомогательных проекций с помощью использования в качестве проецирующих кривых линий (плоских и пространственных).

Изложение начертательной геометрии на проективной основе [5, 6, 31] дало толчок к дальнейшему развитию способов преобразования ортогональных проекций.

Разработанные в последнее время способы, основанные на проективных свойствах, дают наиболее простые решения многих задач.

В России одними из первых работ, в которых использованы свойства коллинеарного преобразования пространства для решения задач начертательной геометрии в ортогональных проекциях, были диссертации О.Ф. Прудаевой и Л.Н. Лихачева.

Представляют интерес также диссертации И.С. Джапаридзе, Ю.А. Харита, Н.В. Белова, К.И. Валькова, Д.Н. Борисова, И.М. Малунцева и др.

Применение топологических преобразований привело к созданию нового способа решения задач по определению линий пересечения различных поверхностей. При этом топологические преобразования дали возможность получить не только простой, но и наглядный способ графических решений. Здесь следует отметить работы Н.К. Грушинской, И.М. Халдеева, Н.А. Малахова.

Несмотря на многообразие способов начертательной геометрии, все они могут быть отнесены всего лишь к нескольким группам. Одним из признаков для объединения может служить единство принципа, положенного в основу того или иного способа преобразования:

1. Изменение относительного положения проецируемой фигуры и плоскостей проекций (при сохранении ортогональности проецирования) лежит в основе классических способов преобразования начертательной геометрии, известных широкому кругу инженерно-технических работников под названием: способ вращения и способ перемены плоскостей проекций.

8

2. Изменение направления проецирования (при неизменных плоскостях проекций) или выбор нового вида проецирования дает обоснование различным способам, объединенным под общим названием способа вспомогательного проецирования¹.
3. Использование коллинеарных свойств пространства привело к созданию способа проективных преобразований.
4. Использование топологических свойств пространства и находящихся в нем геометрических образов положило начало новым способам, которые могут быть сформулированы как способ топологических преобразований, сюда же условно можно отнести и способ квадратичных преобразований.

Рассмотрим более подробно каждый из отмеченных способов.

9