§ 16. Криволинейное проецирование

В последние годы авторами (А.И. Руубель, А.А. Кон, A.M. Тевлин, А.Л. Подгорный, Н.К. Грушинская, М.К. Погребецкая и др.) предложены способы получения вспомогательных проекций с помощью криволинейного проецирования.

При криволинейном проецировании для получения проекций геометрического образа используют кривые линии. При этом проекция пространственной точки определяется как точка пересечения проецирующей линии, проходящей через точку, с плоскостью проекции. Криволинейное проецирование с успехом может использоваться для решения позиционных задач по определению точек встречи линии с поверхностью, а также для нахождения сечения поверхности плоскостью и линии пересечения двух поверхностей.

С позиции криволинейного проецирования линия пересечения поверхности с плоскостью есть криволинейная проекция поверхности на эту плоскость. Аналогично, линия пересечения двух поверхностей есть не что иное, как криволинейная проекция одной поверхности на другую.

Упрощение решения задач посредством криволинейного проецирования достигается за счет преобразования поверхности, произвольно расположенной по отношению к плоскостям проекции (или секущей плоскости) в проецирующую.

Очевидно, чтобы закономерная криволинейная поверхность стала проецирующей, достаточно спроецировать ее в направлении образующих поверхности. Выбор формы проецирующей кривой зависит от формообразующих поверхность линий. Эти кривые могут быть плоскими или пространственными.

Рассмотрим в отдельности эти два варианта криволинейного проецирования.

Криволинейное проецирование плоскими кривыми

Наибольший практический интерес (в смысле простоты геометрических построений) представляет проецирование с помощью дуг окружностей - окружностное проецирование.

Аппарат окружностного проецирования будет определен, если известно положение прямой J - носителя центров проецирующих окружностей и плоскостей проекций.

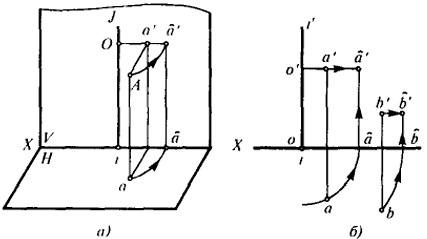
Нахождение окружностной проекции точки А (а(, а'() по данным ортогональным проекциям этой точки, если задан аппарат проецирования,

64

Рис. 59	Рис. 60

показано на рис. 59, а и б. На рис. 59, б показано также нахождение вспомогательной проекции b(, b'( точки В.

Определение окружностных проекций точки ничем не отличается от известных построений способа вращения вокруг осей, перпендикулярных плоскостям проекций.

Окружностное проецирование прямой

В зависимости от взаимного расположения прямой АВ и носителя центров (оси J), прямая на фронтальную плоскость проекции (или на плоскость, параллельную ей и инцидентную J) проецируется:

• а) в проецирующую прямую при АВ ‖ J (рис. 60);
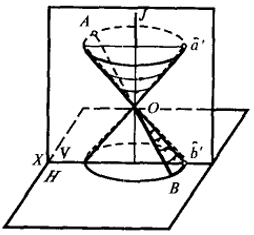
• б) в две полупрямых, равнонаклонных к оси J, когда АВ × J (рис. 61);
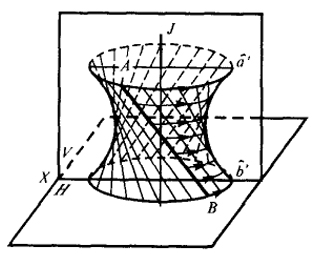
• в) в ветвь гиперболы, если АВ и J скрещиваются (рис. 62).

Чертежи на рис. 60, 61 и 62 дают наглядное представление о виде окружностных проекций прямой и не нуждаются в пояснении. Следует иметь в виду, что с помощью окружностного проецирования кривые второго порядка можно спроецировать в прямую линию. На рис. 63 показано, как эллипс 1, парабола 2 и гипербола 3 проецируются в отрезки, лежащие на прямой SA.

Рис. 61	Рис. 62

65

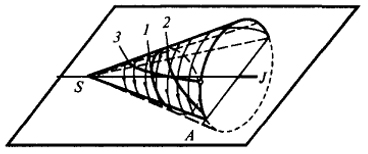
Рис. 63

С помощью окружностного проецирования просто решаются задачи по определению точек встречи прямой с поверхностью вращения и нахождения линии пересечения поверхности вращения с линейчатой поверхностью.

Действительно, используя окружностное проецирование, любую поверхность вращения можно рассматривать как проецирующую поверхность, след которой на плоскость, инцидентную оси центров, совпадает с меридиональной линией, а любую кривую второго порядка - как отрезок прямой, инцидентной образующей конуса вращения, сечением которого является данная кривая.

Иллюстрируем сказанное на конкретных примерах. Пусть требуется определить точки встречи прямой АВ с произвольной поверхностью вращения α. Задачу решить для случая когда:

• а) АВ параллельна оси поверхности α;
• б) АВ пересекает ось поверхности;
• в) АВ и ось поверхности скрещиваются.

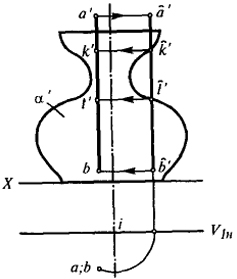
Вариант а (рис. 64). Принимаем ось поверхности вращения (J) за носитель центров проецирующих дуг. Проецируем поверхность α и прямую АВ на плоскость V₁, инцидентную J и параллельную V. При таком аппарате проецирования поверхность вращения по отношению к плоскости V₁ окажется проецирующей, ее след на эту плоскость будет конгруентным фронтальной ортогональной проекции. Окружностная проекция прямой АВ (а'(, b'() будет параллельна i'. Точки пересечения а'<b'< с очерком фронтальной проекции поверхности α - k' и l' - окружностные проекции искомых точек встречи. Обратными построениями находим k', l' и k, l.

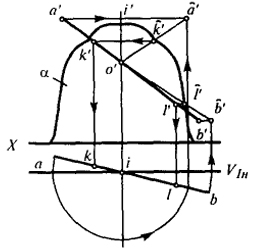
Вариант б (рис. 65). За носитель центров, как и в предыдущем примере, принимаем ось поверхности вращения, аза плоскость проекции - плоскость, инцидентную J и параллельную V. Это обеспечивает перевод поверхности вращения α в проецирующую поверхность, a прямую АВ - в две полупрямые о'а'( и о'b', которые пересекают ортогональную

66

Рис. 64	Рис. 65

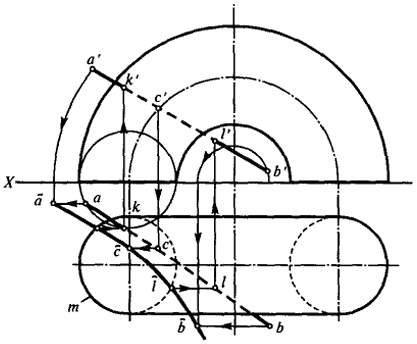
Рис. 66

фронтальную проекцию поверхности вращения в точках k'( и l'(. Зная положение этих точек, находим их ортогональные проекции.

Вариант в (рис. 66). Пусть поверхность вращения α - тор, прямая АВ произвольно расположена в пространстве. Принимаем за носитель центров ось тора, а за плоскость окружностных проекций - горизонтальную плоскость Н.

В этом случае следом торовой горизонтально-проецирующей поверхности будет окружность т, а окружностной проекцией прямой на эту плоскость - гипербола а(с(b(. Точки k( и l( пересечения гиперболы с окружностью будут окружностными проекциями искомых точек. Зная положение точек k< и l< легко находим k, l и k', l'.

67

Криволинейное проецирование пространственными
кривыми

При проецировании пространственными кривыми особый смысл имеет винтовое проецирование, при котором в качестве проецирующих линий берутся винтовые линии с общей осью j и одинаковым шагом Н. Использование винтовых линий позволяет получить вырожденные проекции винтовых поверхностей, что существенно упрощает решение многих позиционных задач.

Получение вспомогательных криволинейных проекций при винтовом проецировании начнем с нахождения проекций точки.

Винтовыми проекциями точки называют точки пересечения винтовой линии, проходящей через заданную точку, с плоскостями проекций. В качестве плоскостей проекций принимаем плоскости Н ⊥ J и V, инцидентную оси J. Обозначим винтовые проекции точки соответственно a^b и а'. Пусть связка винтовых проецирующих линий задана осью J и параметром k (рис. 71, а).

Параметр k определяется зависимостью между углом поворота ψ и осевым перемещением z любой точки винтовой линии, радиус которой r, а угол подъема β:

k = 

z

Ψ

 = 

z

Ψ

 = rtgβ

Каждая точка пространства А при заданных J, Н и k имеет единственные винтовые проекции a^b и a'^b. Пусть a и а' - ортогональные проекции точки с цилиндрическими координатами φ, r, z и проецирующая ее винтовая линия l, k, r (рис. 67, б).

Горизонтальной проекцией траектории перемещения точки А при винтовом проецировании является окружность радиуса r, проведенная

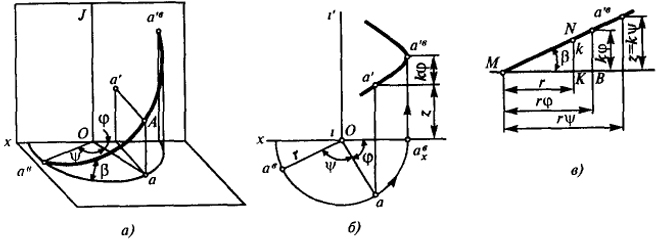
Рис. 67

68

Рис. 68	Рис. 69

из центра О (рис. 67, а и б). Ортогональная горизонтальная проекция точки a^b находится в точке пересечения этой окружности с осью х, апликата точки а'^b равна аппликате z_(·)a_i + kφ.

Для определения величины kφ воспользуемся параметрическим графиком, устанавливающим зависимость между угловым и осевым перемещением точки. При построении параметрического графика воспользуемся следующим свойством винтовой линии: при развертывании цилиндрической поверхности (J, r) принадлежащая ей винтовая линия изобразится гипотенузой MN прямоугольного треугольника MNK c углом при вершине М равным β и катетами MN и KN соответственно равными r и k (рис. 67, в). Чтобы найти величину осевого перемещения точки при повороте ее на угол φ (что соответствует перемещению ее по винтовой линии из исходного положения в положение, инцидентное плоскости V), достаточно на прямой МК отложить отрезок, равный rφ, и из полученной точки В восставить перпендикуляр Ba'^b до пересечения его с гипотенузой MN. Отрезок Ва'^b укажет величину осевого смещения точки.

Полученный график позволяет находить по заданным ортогональным проекциям точки ее винтовые проекции и решать обратную задачу - по винтовым проекциям определять ортогональные проекции, т.е. рассмотренный параметрический график выполняет функции диаграммы в ранее рассмотренных способах С.М. Колотова и Д.Н. Борисова или "ключевого" треугольника в способах В.П. Левина, Р.С. Бриллинга, И.Г. Виницкого.

69

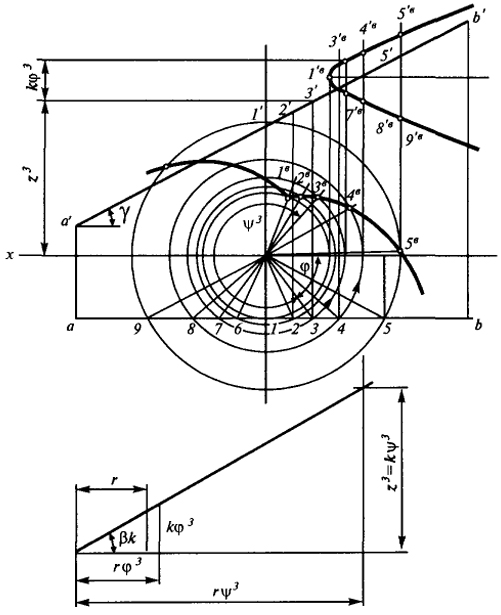
Рис. 70

Винтовое проецирование прямой. Как и в случае окружностного проецирования, вид проекции прямой будет зависеть от взаимного расположения прямой АВ и оси винтовых проецирующих линий J¹:

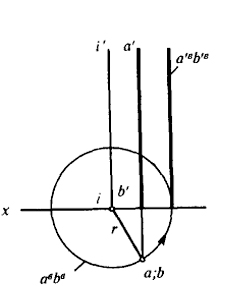
• а) если АВ параллельна оси J, то она спроецируется на плоскость V в прямую а'^вb'^в параллельную i', и на плоскость Н - в окружность c^вb^в радиуса r с центром i (рис. 68);
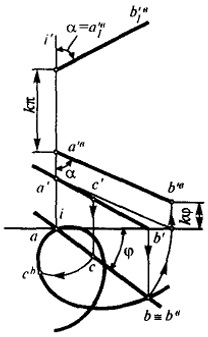
• б) если прямая АВ пересекает ось J, то ее проекциями будут: на плоскости V - две полупрямых a'^вb'^в и а'^в₁b'^в₁, а на плоскости H - архимедова спираль (рис. 69);
• в) прямая АВ, скрещивающаяся с осью J, проецируется на плоскость V кривую 5'^в1'^в9'^в, уравнения которой в системе xOz имеют вид: х = rsec(δ - φ); z = rtg(δ - φ)tgγ + kφ + z.

70

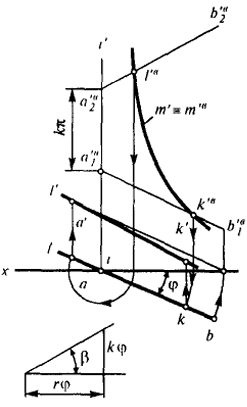
Рис. 71

На плоскость Н прямая АВ проецируется в эвольвенту окружности (при этом в зависимости от угла γ наклона прямой к плоскости H эвольвента может быть удлиненной γ > β, укороченной γ < β или нормальной γ = β (рис. 70).

Винтовое проецирование винтовых поверхностей позволяет получить вырожденные проекции этих поверхностей, т.е. винтовая поверхность Ω (i, k, l) с осью инцидентной оси проецирования, имеет винтовые проекции l'^в ≡ l' на плоскость V и l^в ≡ l на плоскость H.

В качестве иллюстрации возможностей винтового проецирования рассмотрим задачу на определение точек встречи прямой АВ с винтовой поверхностью Ω.

Поверхность Ω задана главным меридианом т', а прямая АВ пересекает ось этой поверхности (рис. 71). Принимаем за ось винтового проецирования ось данной поверхности. Фронтальную плоскость проекции проводим через ось проецирования, тогда винтовая проекция поверхности Ω на фронтальную плоскость (т'^в) окажется инцидентной т' (m'^в ≡ т' ≡ Ω'^в). Фронтальными проекциями прямой АВ будут две полупрямых а'^в₁b'^в₁ и a'^в₂b'^в₂. Точки k'^в и l'^в, в которых а'^в₁b'^в₁ и а'^в₁b'^в₁ пересекают m', будут вспомогательными винтовыми проекциями точек встречи; обратными построениями находим их ортогональные проекции.

71