При решении некоторых задач на пересечение тел бывает целесообразно использовать одновременно как параллельное, так и центральное вспомогательное проецирование.
Сочетание различных способов проецирования позволяет значительно сократить количество графических построений, а следовательно, проще решить задачу.
Проф. С.М. Колотов, внесший большой вклад в разработку и развитие метода вспомогательного проецирования [16], назвал способ, в котором при решении задач применяются два различных способа проецирования двойным вспомогательным проецированием.
На примере определения линии пересечения двух пирамид, произвольно расположенных в пространстве, покажем использование способа двойного вспомогательного проецирования (рис. 58).
Очевидно, эта задача может быть решена путем построения только одной центральной вспомогательной проекции обеих пирамид на плоскость основания ABC пирамиды SABC.
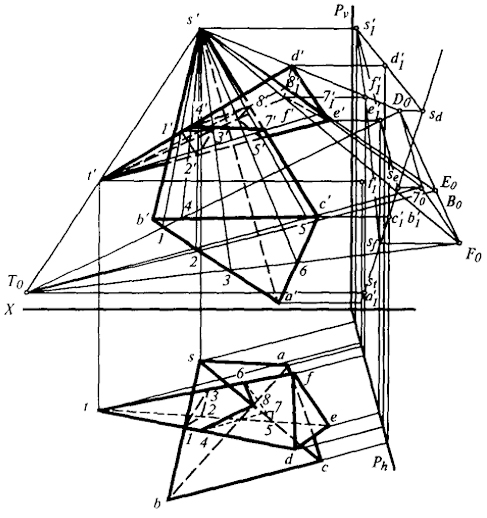
Рис. 58
62
Построение центральной вспомогательной проекции на основание ABC из центра S потребовало бы очень громоздких построений. Количество их можно значительно сократить, если предварительно косоугольно спроецировать обе пирамиды на некоторую горизонтально-проецирующую плоскость.
В произвольном месте чертежа проведем следы такой плоскости Ph и Pv Направление косоугольного проецирования принимаем параллельно ребру ВС. В этом случае основание пирамиды ABC спроецируется в прямую а'1с'1, а ее вершина - в точку s'1. Проекцией пирамиды TDEF будет t'1d'1e'1f'1.
Центрально-проецирующие лучи, проходящие через вершину S и проецирующие пирамиду TDEF на плоскость основания ABC, спроецируются в прямые s'1st, s'1s0, s'1se, s'1sf.
Найдя точки st, sd, se, sf в которых косоугольные проекции этих лучей пересекают проекцию основания пирамиды ABC на горизонтально-проецирующей плоскости, легко определить их положение на фронтальной проекции этого основания.
Для этого достаточно найденные точки обратным проецированием возвратить в их первоначальное положение.
Из точек st, sd, se и sf проводим прямые, параллельные фронтальной проекции ребра ВС, до пересечения с фронтальными проекциями центрально-проецирующих лучей, проходящих через точки t', d', e', f'. Соединив между собой найденные точки пересечения Т0, D0, E0, получим вспомогательную фронтальную проекцию пирамиды TDEF на основании ABC пирамиды SABC.
Пересечение ребер Т0D0, T0E0, T0F0 со сторонами треугольника a'b'c' обозначим точками 1, 2, 3, 4, 5, 6. Соединив эти точки с s', находим точки 1', 2', 3', 4', 5', 6' в пересечении с прямыми t'd', t'e', t'f'. Полученные точки являются искомыми фронтальными проекциями пересечений ребер пирамиды TDEF с гранями пирамиды SABC.
Для определения точек пересечения ребра sc пирамиды SABC с гранями пирамиды TDEF построим изображение фиктивного ребра T0c', которое пересекает основание D0E0F0 в точках 70 и 80. Этим точкам соответствуют точки 7'1 и 8'1 на основании d'e'f'.
Соединив t' с 7'1 и 8'1 определяем пересечение прямых t'7'1 и t'18'1 с s'c'.
Найденные точки 7' и 8' будут искомыми фронтальными проекциями точек встречи ребра SC с гранями пирамиды TDEF.
Определив все необходимые точки пересечения пирамиды, проводим линии пересечения и определяем их видимость.
63
