Использование в качестве вспомогательной плоскости проекции биссекторной плоскости дает возможность существенно облегчить решение ряда позиционных задач начертательной геометрии.
58
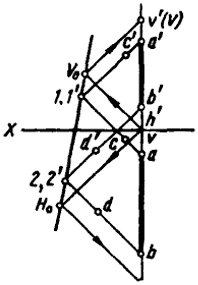
Рис. 55
Получение более простых решений основано на свойствах проекций точек, лежащих в биссекторной плоскости.
Любая точка биссекторной плоскости удалена на одинаковые расстояния от двух координатных плоскостей проекций, поэтому, если эта плоскость проходит через второй и четвертый октанты, горизонтальная и фронтальная проекция точек совпадают. Следовательно, если продолжить горизонтальную и фронтальную проекции прямой до их взаимного пересечения, то мы получим точку, лежащую в биссекторной плоскости.
Если имеются две проекции плоских фигур, то пересечение разноименных проекций прямых, лежащих в плоскости фигур, образует ряд точек, лежащих на одной прямой. Эта прямая является линией пересечения плоскости фигуры с биссекторной плоскостью. Она может быть получена так же, как проекция плоской фигуры на биссекторную плоскость, если за направление проецирования принять направление любой прямой, лежащей в проецируемой фигуре1.
Возможность практического использования в качестве вспомогательной плоскости проекции биссекторной плоскости проследим на решении следующих задач.
Задача 1. Найти следы профильной прямой АВ (рис. 55). Эта задача обычно решается с помощью профильной проекции, но ее можно решить и путем вспомогательного проецирования на биссекторную плоскость.
Заключим прямую АВ в произвольную плоскость. Для этого через точку А (или любую другую точку, лежащую на прямой) проводим произвольную прямую АС. Проецируем полученную плоскость на биссекторную плоскость второго и четвертого октантов в направлении прямой АС. Для осуществления операции проецирования достаточно найти точку взаимного пересечения разноименных проекций прямой АС 1 и 1', для получения второй точки 2, 2' прямой через точку В проводим прямую BD параллельно АС до пересечения ее с биссекторной плоскостью.
Имея прямую 1 2 (биссекторный след плоскости), легко определить следы профильной прямой АВ.
59
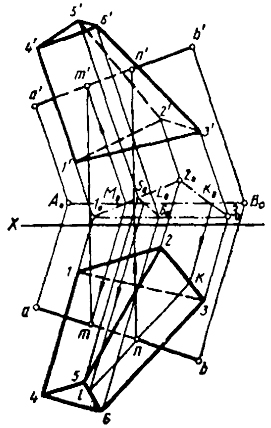
Рис. 56
Положение фронтальной проекции горизонтального следа и горизонтальной проекции фронтального следа нам известно. Проводим через h' прямую h'H0‖a'c' до пересечения с прямой 1 2 в точке Н0 и через точку Н0 прямую H0h. Пересечение этой прямой с горизонтальной проекцией ab определит горизонтальный след Н. Для нахождения фронтального следа через v проводим прямую vV0 параллельно ас до пересечения ее прямой 1 2, из полученной двойной точки проводим V0v'. Фронтальный след V находится пересечением V0v' с a'b'.
Задача 2. Определить точки встречи прямой АВ с гранями усеченной пирамиды (рис. 56). Проецируем пирамиду 1, 2, 3, 4, 5, 6 и прямую АВ на биссекторную плоскость в направлении ребра пирамиды 1 4. Вспомогательная проекция пирамиды определяется двумя подобными треугольниками 102030 и 105060, проекция прямой - прямой А0В0.
Точка M0 пересечения А0В0 со стороной треугольника 1020 будет вспомогательной проекцией одной из искомых точек встречи, ортогональные проекции которой т и т' находим с помощью обратных лучей. Другая точка встречи может быть найдена с помощью прямой KL, лежащей на грани пирамиды 2, 3, 6, 5. Определяем горизонтальную проекцию kl. Пересечение kl с аb дает искомую горизонтальную проекцию точки п. По п находим п'. Данная задача могла быть решена элементарно способом введения секущих плоскостей. Мы показали ее лишь для пояснения способа построения вспомогательной проекции на биссекторную плоскость. Преимущество использования биссекторной плоскости проявляется при решении более громоздких задач. Простота решения может быть продемонстрирована на примере построения линий пересечения кругового цилиндра и призмы с произвольно расположенными осями (рис. 57).
Проецируем цилиндр и призму на биссекторную плоскость. Направление проецирования принимаем параллельным образующей цилиндра. В этом случае цилиндрическая поверхность окажется проецирующей. Эллипс L0K0E0 представляет след цилиндрической поверхности на биссекторной плоскости.
60
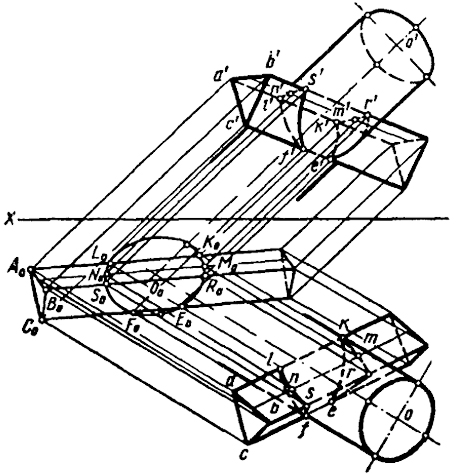
Рис. 57
Следовательно, участки эллиптической кривой K0R0E0 и F0S0L0 являются вспомогательной проекцией линий пересечения граней призмы с поверхностью цилиндра, полученной при заданном направлении проецирования.
С помощью обратных лучей легко построить ортогональные проекции этих линий.
Для точного построения линий пересечения указанных шести точек явно недостаточно. В качестве дополнительных точек можно взять любое количество точек на эллипсе и направлением обратного проецирования перевести их на ортогональные проекции.
В качестве примера таких построений на чертеже показано нахождение точек М0 и N0, в которых пересекается произвольная прямая, параллельная ребру призмы и лежащая на грани АВ с цилиндрической поверхностью.
Рассматривая рис. 57, можно сделать вывод, что решение задачи на пересечение тел путем вспомогательного параллельного проецирования на биссекторную плоскость выгодно отличается от решения задач другими способами как по количеству графических построений, так и по их простоте.
61
1
Исключение составляет только прямая, параллельная биссекторной плоскости.
