§ 13. Комбинированный способ получения
вспомогательных проекций

P.M. Минин в своей диссертации предложил способ получения неискаженного вида вспомогательной проекции на плоскости общего положения.

К этому же периоду относится работа Н.Т. Чувикова [32], посвященная тому же вопросу. В основу предлагаемых способов обоими авторами положены, по существу, одинаковые предпосылки, поэтому окончательные результаты получаются также одинаковыми. Последнее обстоятельство делает возможным объединить оба способа в один, сохранив за ним название, предложенное Н.Т. Чувиковым¹.

Проецирующий аппарат комбинированного способа допускает любое проецирование (прямоугольное, косоугольное, центральное) на произвольно выбранную вспомогательную плоскость с последующим совмещением этой плоскости с плоскостью чертежа. При этом, в отличие от способа проф. С.М. Колотова, необходимые построения осуществляются без помощи диаграммы.

Выше было отмечено, что комбинированный способ допускает любой способ проецирования. Остановимся лишь на параллельном проецировании, так как с его помощью можно привести ортогональные проекции к новому, более удобному для решения многих задач, виду.

Центральное проецирование затрагиваться не будет, так как его использование ограничено чрезвычайно узким кругом задач и применяется в основном для преобразования ортогональных проекций в аксонометрические.

В основе графических построений, принятых в комбинированном способе, лежит известное из элементарной геометрии положение о том, что точку можно рассматривать как результат пересечения трех плоскостей.

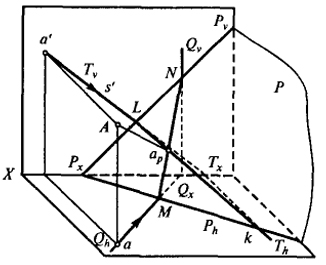
Косоугольное проецирование на произвольно выбранную плоскость. Для получения вспомогательной проекции точки на произвольно выбранную плоскость по заданному направлению комбинированным способом поступают следующим образом. Через прямую Аа_p, проецирующую точку А на плоскость Р (рис. 46), проводим две проецирующие плоскости Q и Т. Плоскость Q пересекает плоскость Р по прямой MN, а плоскость Т по прямой KL. Взаимное пересечение

51

Рис. 46	Рис. 47

прямых MN и KL даст искомую проекцию а_р точки A на плоскость Р по заданному направлению проецирования S.

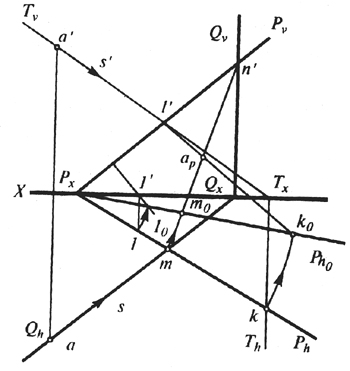
Чтобы получить неискаженную косоугольную проекцию, плоскость Р следует совместить с плоскостью чертежа. На рис. 47 все построения выполнены на эпюре.

Совмещенное положение следа P_h0 определено с помощью точки 1. Совмещенное положение прямых MN и KL получено перемещением точек т и k, в которых плоскости Q и Т пересекают след P_h, на совмещенное положение следа P_h0. Совмещенное положение точки а_р находится пересечением совмещенных прямых k₀l' и m₀n'.

Сущность комбинированного способа и целесообразность его применения могут быть легко выяснены на примере определения точки встречи прямой с плоскостью.

Эта задача чрезвычайно распространена, а подчас она является "ключом" при решении более сложных вопросов начертательной геометрии.

Обычно при решении этой задачи в системе двух взаимно перпендикулярных плоскостей проекций Н и V мы получим две ортогональные проекции точки встречи прямой с плоскостью. Практически больший смысл представляет зафиксировать положение найденной точки не относительно плоскостей Н и V, а непосредственно на плоскости Р. Комбинированный способ дает возможность получить именно такой ответ.

Для этого, очевидно, необходимо спроецировать на плоскость Р прямую АВ в ее собственном направлении (рис. 48).

52

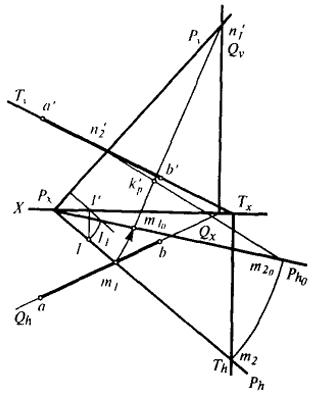
Рис. 48

Ход геометрических построений при решении задачи будет следующим:

• 1) плоскость Р совмещаем с плоскостью чертежа;
• 2) через проекцию прямой ab проводим след Q_h горизонтально-проецирующей плоскости, а через а'b' след T_v фронтально-проецирующей плоскости;
• 3) определяем совмещенное положение прямых M₁N₁ и M₂N₂ - линий пересечения плоскости Р с плоскостями Q и Т;
• 4) искомая точка К_р определится взаимным пересечением прямых m₁₀n'₁ и m₂₀n'₂.

Мы видим, что для определения точки встречи прямой с плоскостью нет необходимости в определении ортогональных проекций.

Последнее обстоятельство дает возможность при решении задач на построение плоских сечений тел комбинированным способом значительно уменьшить количество геометрических построений, необходимых для решения таких задач обычным путем.

Проследим достоверность этого утверждения на примере решения задачи по определению натуральной величины сечения пятигранной призмы, произвольно расположенной в пространстве плоскостью общего положения (рис. 49).

Направление проецирования принимаем параллельным ребрам призмы. В этом случае решение задачи аналогично предыдущей. Так как ребра призмы параллельны, то, очевидно, будут параллельны между собой и совмещенные положения вспомогательных прямых, с помощью которых определяют точки встречи ребер с плоскостью. Поэтому достаточно определить направление вспомогательных прямых для одного ребра; точки встречи остальных ребер с плоскостью получим, проводя прямые, параллельные этим прямым.

На рис. 49 показаны построения точки e_р, в которой ребро Е пересекает плоскость Р.

Для нахождения точек a_p, b_p, c_p, d_p через точки 1', 2', 3', 4' проводим прямые, параллельные 5'е_р, а через точки 6₁, 7₁, 8₁, 9₁ - прямые, параллельные

53

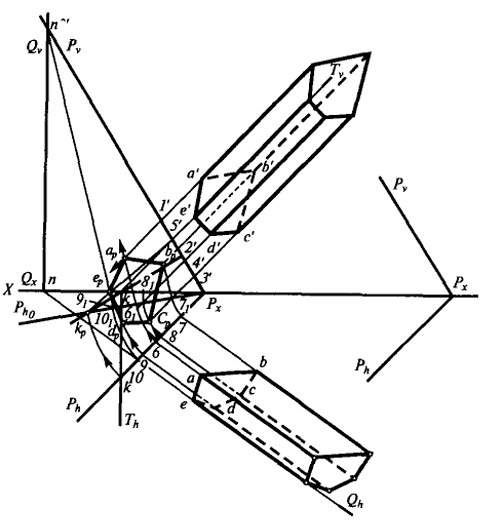
Рис. 49

10₁е_р. Пересечение этих прямых определит положение искомых точек.

Для того чтобы все построения были видны яснее, плоскость Р смещена параллельно влево.

Следует иметь в виду, что пятиугольник a_pb_pc_pd_pe_p представляет истинную величину сечения призмы. В этом отношении решение задачи комбинированным способом быстрее приводит к цели, чем решение ее по способу проф. С.М. Колотова (задача 3, § 10), где определение истинной величины потребует дополнительных построений.

Иногда бывает целесообразно при использовании комбинированного способа для решения задач по определению истинной величины сечения тела плоскостью направление проецирования принимать параллельным горизонтали или фронтали плоскости.

Задача. Даны конус с эллиптическим основанием, лежащим в плоскости Н, и секущая плоскость Р. Определить натуральную величину сечения (рис. 50).

Превратим плоскость общего положения Р в косоугольнофронтально-проецирующую. Для этого достаточно отказаться от ортогонального направления проецирования и принять его параллельным горизонтали плоскости Р.

54

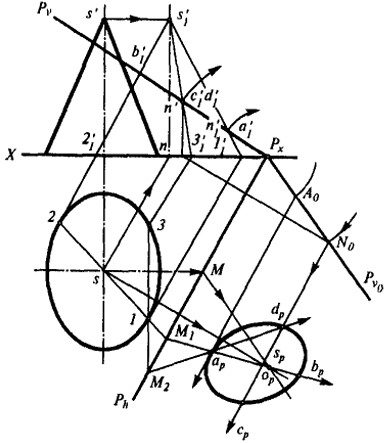
Рис. 50

Полученный треугольник 1'₁s'₁2'₁ будет новой вспомогательной проекцией конуса. Отрезок a'₁b'₁ является вспомогательной фронтальной проекцией сечения конуса, он может быть принят за диаметр эллипса сечения. Сопряженный ему диаметр будет проецироваться в точку с'₁, делящую пополам расстояние между а₁ и b'₁.

Совместив плоскость Р с плоскостью H, можно определить величину другого сопряженного диаметра. Характер необходимых геометрических построений при этом будет следующий.

Совмещенное положение следа P_v0 находим с помощью точки N, фронтальная проекция которой п' совпадает с с'₁; через совмещенное положение точки N₀ пройдет след P_v0 и совмещенная горизонталь, на которой будет находиться один из сопряженных диаметров и центр искомого эллипса.

Совмещенное положение и размеры сопряженных диаметров определяются с помощью точки S_p.

Считая прямую 12 горизонтальным следом плоскости, проходящей через вершину конуса S, получим точку схода М₁ следов этой плоскости в системе

P

H

. Второй след пройдет через точки S_p и М₁ и определит направление второго сопряженного диаметра и положение О_р - центра искомого эллипса.

Размеры сопряженных диаметров могут быть найдены по концевым точкам. Одна из них а_р находится в пересечении прямой M₁S_p с совмещенной

55

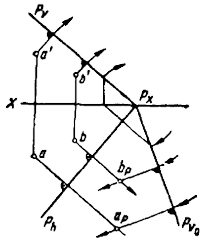
Рис. 51

горизонталью, проходящей через точку А. Зная а_р, легко определить положение b_р. Величина второго диаметра, сопряженного с первым, может быть определена при помощи имеющейся на чертеже косоугольной проекции конуса на плоскости V. Прямая s'₁c'₁ есть косоугольная проекция тех двух образующих конуса, в плоскости которых лежит искомый диаметр.

Образующая конуса s3 и точка 1 определяют плоскость. Прямая 1 3 является горизонтальным следом этой плоскости; M₂ - точка схода следов. Прямая М₂а_р (след плоскости 1s3 на плоскость Р), пересекая прямую N₀c_p, дает искомую точку; d_p - конец второго сопряженного диаметра-эллипса, которым определяется натуральный вид сечения. Зная величину и положение сопряженных диаметров, легко построить эллипс¹.

Прямоугольное вспомогательное проецирование. Все проецирующие лучи при прямоугольном проецировании будут перпендикулярны вспомогательной плоскости проекции. Следовательно, их проекции будут перпендикулярны соответствующим следам плоскости. Это свойство сохраняется и в совмещенном положении, поэтому построения, которые нужно выполнить для нахождения совмещенного положения проекции точки при прямоугольном вспомогательном проецировании, значительно упрощаются.

Рис. 51 дает полное представление о построении прямоугольных вспомогательных проекций точек A и В в совмещенном состоянии.

Использование в комбинированном способе прямоугольного вспомогательного проецирования дает возможность получить неискаженный вид вспомогательной проекции, поэтому комбинированный способ можно применять при решении не только позиционных, но и метрических задач. Характер графических построений при этом не меняется. Необходимо только выбрать правильное положение вспомогательной плоскости проекции, которое определяется условиями задачи.

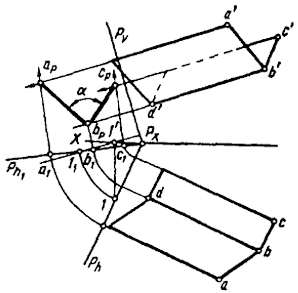
Задача 1. Определить расстояние между скрещивающимися прямыми АВ и CD (рис. 52).

В этой задаче следует применить прямоугольное проецирование. Положение вспомогательной плоскости проекции Р выбирается так, чтобы одна из прямых проецировалась на нее в точку. Затем плоскость Р совмещается с плоскостью чертежа.

56

Рис. 52	Рис. 53

Искомое расстояние определяется величиной перпендикуляра, опущенного из c_pd_p на a_pd_p.

Задача 2. Определить угол между плоскостями Q(DB × AB) и S(DB × CB) (рис. 53).

Вспомогательную плоскость проекции выбираем перпендикулярной прямой BD, по которой пересекаются плоскости Q и S. Проецирование ведем по направлению BD. Полученная после совмещения проекция угла a_pb_pc_p и будет искомой величиной угла а между плоскостями Q и S.

Применение в комбинированном способе прямоугольного проецирования целесообразно для решения громоздких позиционных задач.

Задача 3. Определить линию пересечения цилиндра и призмы, произвольно расположенных в пространстве (рис. 54).

Решение этой задачи геометрическим способом (сечением вспомогательными плоскостями) потребует большого количества вспомогательных построений.

Использование классических способов вызовет необходимость построения минимум двух вспомогательных проекций.

Применяя комбинированный способ, можно обойтись только одной вспомогательной проекцией. Действительно, если выбрать вспомогательную плоскость проекций Р, перпендикулярную оси цилиндра, а за направление проецирования принять направление оси цилиндра, то цилиндрическая поверхность окажется проецирующей и цилиндр спроектируется в окружность.

Построения новой вспомогательной проекции цилиндра и призмы на плоскость Р в совмещенном положении выполнены по аналогии с рис. 51.

57

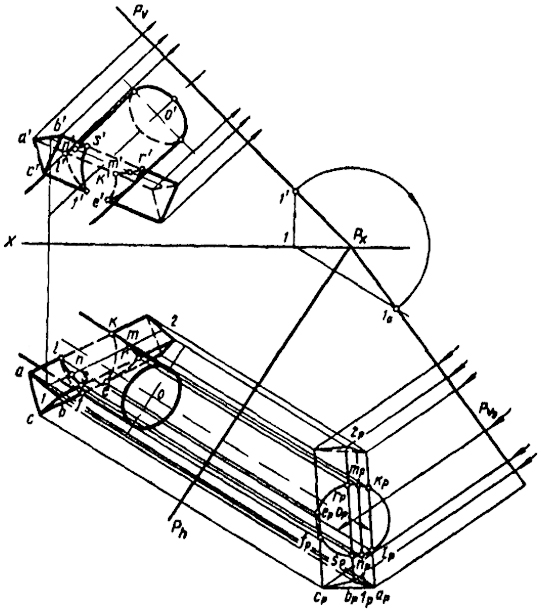
Рис. 54

Точки k_p, l_p, s_p, f_p, e_p, r_p являются совмещенными вспомогательными проекциями точек встречи ребер призмы с поверхностью цилиндра. Чтобы найти их ортогональные проекции, воспользуемся обратными лучами. Для более точного построения кривых линий пересечения можно взять любое количество дополнительных точек, хотя бы точки т_p и п_p. Их ортогональные проекции находятся так же, как и для точек k, r, с той лишь разницей, что предварительно приходится определять проекции прямой 1 2 на грани призмы.

58