§ 12. Прямоугольное проецирование
на две плоскости, пересекающиеся
не под прямым углом

Идея прямоугольного проецирования на две плоскости, пересекающиеся не под прямым углом, не является новой, она была высказана еще Г. Монжем [21]. Но говоря о принципиальной возможности такого проецирования, Монж отрицал целесообразность его практического использования, ссылаясь на то, что если угол между плоскостями "будет очень тупым, то угол, образуемый перпендикулярными плоскостям проекций прямыми, окажется очень острым; на практике же маленькие ошибки могут вызвать очень большую неточность в определении положения точки". С этим утверждением нельзя не согласиться, но в то же время для решения некоторых задач бывает целесообразно спроецировать пространственную фигуру прямоугольно на плоскость, выгодно расположенную по отношению к фигуре, но наклонную к одной из координатных плоскостей. Прямоугольное проецирование в косоугольной системе плоскостей проекций является частным случаем способа вспомогательного проецирования, изложенного в § 12 данной главы (способ проф. С.М. Колотова).

Наиболее подробно способ прямоугольного проецирования рассмотрен в работах Р.С. Бриллинга, В.П. Левина и И.Г. Виницкого.

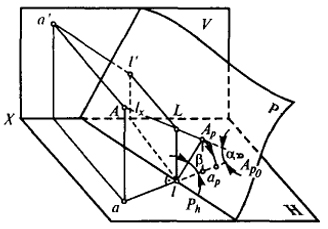
Сущность способа прямоугольного проецирования в косоугольной системе плоскостей может быть понятна из рассмотрения рис. 42, на котором показано построение вспомогательной проекции точки А на плоскость Р.

Плоскость Р, наклонную к H, назовем вспомогательной плоскостью проекций; след Р_h - вспомогательной осью; прямую АА_p - вспомогательно-проецирующей прямой; А_р - вспомогательной проекцией точки А.

47

Рис. 42	Рис. 43

Из рассмотрения рис. 42 можно сделать следующие выводы:

1. Основная и вспомогательная проекция точки располагаются на одном перпендикуляре к вспомогательной оси.
2. Расстояние вспомогательной проекции точки от вспомогательной оси проекции равно умноженному на cos α расстоянию от основной плоскости проекции точки скрещивания (L) прямой АА_p с P_h.

А_р0 l = l'l_xcosα.

Установленная зависимость дает возможность сравнительно просто определить прямоугольную вспомогательную проекцию точки на плоскость общего положения.

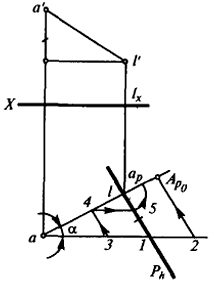
Если даны точки А и плоскость Р, определяемая следом P_h и углом наклона β к горизонтальной плоскости проекции (рис. 43), то для построения первичной и вторичной вспомогательных проекций точки А необходимо через горизонтальную проекцию а провести прямую, перпендикулярную P_h, на этой прямой отложить от точки пересечения ее со следом P_h отрезок lА_p0 = l'l_xcosα. Величина lА_p0- может быть определена графически с помощью прямоугольного треугольника. Один из катетов треугольника совпадает с прямой al. Величина острого угла при вершине a α = (90º - β). Прямая, проведенная через точку а под заданным углом α к al, пересекает P_h в точке 1.

В полученном треугольнике a1l катет l1, совпадающий с P_h, равен разности аппликат A_A-Z_L.

Для нахождения А_р0 на гипотенузе a1 откладываем отрезок 1 2, равный величине Z_L(l'l_x). Через полученную точку 2 проводим прямую 2А_Р0 параллельно P_h до пересечения ее с прямой al.

48

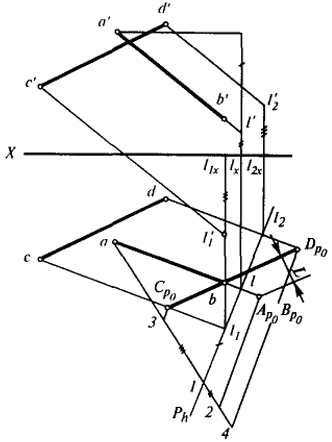
Рис. 44

Треугольник a1l служит основанием для графического определения отрезка lA_p0, является "ключом" к построению вспомогательных проекций любой совокупности точек¹.

Ниже приведены решения типовых задач начертательной геометрии способом прямоугольного проецирования на вспомогательную плоскость.

Задача 1. Определить расстояние между скрещивающимися прямыми АВ и CD (рис. 44).

Вспомогательную плоскость выбираем перпендикулярной прямой АВ. Направление проецирования принимаем параллельным этой прямой. Тогда горизонтальный след P_h вспомогательной плоскости будет перпендикулярен ab. Строим вспомогательный треугольник a1l, у которого катет l1 совпадает с P_h и по величине равен разности аппликат точек А и L.

Для определения проекций А_p0 и B_p0 на направлении гипотенузы a1 откладываем отрезок 1 2, равный l'l_х. Через точку 2 проводим прямую 2A_p0B_p0 параллельно P_h.

49

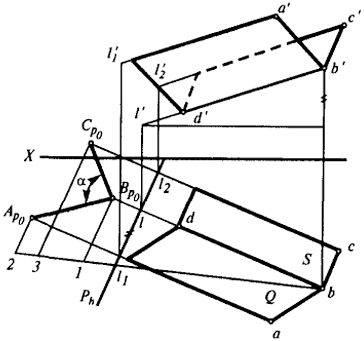
Рис. 45

Построение вспомогательной проекции прямой CD ясно из чертежа.

Через точки С и D проводим прямые, параллельные горизонтальной проекции направления проецирования до пересечения с Р_h в точках l₁ и l₂, и по l₁ и l₂ определяем l_1x, l'₁ и l_2x, l'₂; величины l_1xl'₁ и l_2xl'₂ откладываем по направлению гипотенузы от точки ее пересечения со следом P_h¹.

Из полученных точек 3 и 4 проводим прямые, параллельные P_h до пересечения их с соответствующими горизонтальными проекциями вспомогательно-проецирующих лучей.

Величина перпендикуляра, опущенного из точки А_р0 B_р0 на прямую C_р0, D_р0, укажет искомое расстояние.

Задача 2. Определить угол между плоскостями Q(BD × AB) и S(BD × CB) (рис. 45).

Решение задачи аналогично предыдущей.

Проецируем линию пересечения плоскостей BD на вспомогательную плоскость Р, перпендикулярную BD.

Направление проецирования совпадает с направлением прямой BD.

Находим вспомогательные проекции прямых, проходящих через точки А, В и С. Угол А_р0B_р0C_р0, равный α, будет искомым.

50