В отличие от способа, предложенного проф. С.М. Колотовым, проецирование ведется не на специально выбранную плоскость, а непосредственно на заданные координатные плоскости.
При таких условиях вспомогательные проекции получают косоугольным или центральным проецированием. Ниже на примерах решения конкретных задач разберем оба случая.
44
 |
 |
| Рис. 39 |
Рис. 40 |
Косоугольное вспомогательное проецирование. Допустим, необходимо определить точку встречи прямой АВ с плоскостью общего положения Р.
Известно, что задача определения точки встречи прямой с плоскостью решается элементарно просто (без каких-либо дополнительных построений), если прямая или плоскость занимает проецирующее положение.
Мы знаем, что плоскость или прямая называются проецирующими, если они параллельны проецирующему лучу. Следовательно, для перевода прямой или плоскости общего положения в проецирующее (при неизменном положении плоскостей проекции) можно пользоваться двумя путями: переместить ее в пространстве так, чтобы она оказалась параллельной проецирующему лучу, или выбрать новое направление проецирования, параллельное заданной прямой (плоскости).
Обычно при использовании классических методов преобразования для перевода прямой или плоскости, произвольно расположенных в пространстве, в положение проецирующих идут по первому пути, но можно решить эту задачу иначе - выбрать новое направление проецирования, параллельное плоскости или прямой.
Изменение направления проецирования допускает два возможных варианта решения поставленной задачи.
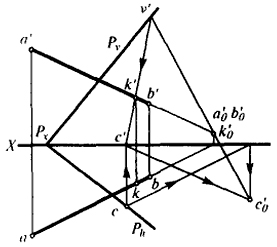
1-й вариант (рис. 39). Направление проецирования принимаем параллельным горизонтами плоскости Р.
При таком проецировании плоскость Р окажется фронтально-проецирующей, а новая вспомогательная проекция прямой АВ на плоскость V изобразится отрезком a'0b'0. Очевидно, точка пересечения вспомогательной проекции a'0b'0 со следом Pv (k'0) определит вспомогательную
45
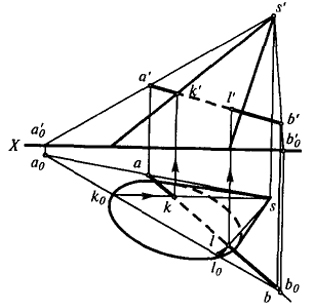
Рис. 41
проекцию точки встречи прямой АВ с плоскостью Р, ортогональные проекции которой k и k' находятся с помощью обратного луча.
2-й вариант (рис. 40). Направление проецирования принимаем параллельным прямой АВ. В этом случае прямая спроецируется на плоскость V в точку a'0b'0, которая будет также вспомогательной фронтальной проекцией точки пересечения данной прямой с плоскостью Р(k'0).
Для нахождения ортогональных проекций точки К следует взять произвольную точку С на Ph, построить ее косоугольную проекцию, c'0 · c'0 и фронтальный след Pv определяют косоугольную проекцию плоскости Р. Соединив с'0 с k'0, получим косоугольную проекцию прямой, лежащей в плоскости Р и проходящей через точку К. Продолжая c'0k'0 до пересечения с Pv, получим фронтальный след прямой v'. Соединив его с с', найдем фронтальную проекцию прямой c'k'. Пересечение v'c' с а'b' даст фронтальную проекцию k' искомой точки К'.
Центральное вспомогательное проецирование. В предыдущем параграфе отмечалось, что в ряде случаев целесообразно в качестве вспомогательного проецирования использовать центральные проекции.
Пусть требуется определить точки пересечения произвольной прямой АВ с конической поверхностью (рис. 41).
Для решения данной задачи удобно воспользоваться центральным проецированием на плоскости Н. За центр проецирования принимаем вершину конуса S. Центральная проекция конической поверхности будет совпадать с криволинейным очерком горизонтальной проекции, а вспомогательная центральная проекция прямой определится отрезком a0b0. Точки k0 и l0, в которых отрезок a0b0 пересекает очерк основания
46
конической поверхности, будут вспомогательными центральными проекциями искомых точек пересечения. Зная k0 и l0, легко найти горизонтальные проекции k и l, а по ним k' и l'.
Произвольное косоугольное и, особенно, центральное проецирование не позволяют решать метрических задач.
Исключение представляет только такое косоугольное проецирование плоскости, при котором все фигуры, расположенные в ней, и их взаимное расположение проецируются на плоскость проекций без искажения.
47
