§ 10. Параллельное и центральное
проецирование на специально
выбранную плоскость

Выше было отмечено, что вспомогательные проекции можно получить путем центрального или параллельного проецирования как на одну из основных координатных плоскостей, так и на специально выбранную плоскость. В последнем случае полученные на этой плоскости проекции переводятся на координатную плоскость путем совмещения¹.

В наиболее общем виде метод вспомогательного проецирования предусматривает выполнение ряда последовательных операций. Первая из них сводится к выбору вспомогательной плоскости проекций и направления или способа проецирования.

Затем на вспомогательной плоскости строят проекцию геометрического образа, что иногда связано с нахождением большого количества точек встречи проецирующих прямых с плоскостью.

Использование полученной вспомогательной проекции для решения задач не всегда возможно, так как ее проекции на координатные плоскости дают искаженный вид предмета.

Чтобы иметь неискаженный вид вспомогательной проекции, необходимо выполнить дополнительные построения для совмещения вспомогательной плоскости проекции с основной координатной плоскостью или с плоскостью, параллельной ей. Таким образом, решение задачи (в особенности, если она носит метрический характер) способом вспомогательного проецирования на специально выбранную плоскость связано с большим количеством дополнительных и часто громоздких построений.

Проф. С.М. Колотов предложил [15] новый способ построения вспомогательных проекций, который состоит в том, что при решении метрических задач вспомогательные проекции строятся сразу на совмещенном положении плоскости, используя для этой цели основные

33

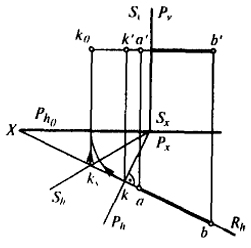
Рис. 27

ортогональные проекции, выбранное направление проецирования и положение следов вспомогательной плоскости.

Для решения позиционных задач нет необходимости получать истинные размеры проекций, поэтому в данном случае С.М. Колотов предлагает ограничиться построением вспомогательных проекций непосредственно на плоскости в ее несовмещенном положении, указывая при этом только одну (фронтальную) проекцию.

Получение совмещенного положения вспомогательной проекции, обеспечивающего ее неискаженный вид, имеет смысл только при прямоугольном проецировании.

Поэтому изложение способа проф. С.М. Колотова начнем именно с этого частного случая проецирования.

Прямое вспомогательное проецирование. В основе способа вспомогательного проецирования лежит задача определения точки встречи прямой, произвольно расположенной в пространстве, с плоскостью общего положения.

Пусть требуется определить точку встречи К прямой АВ с плоскостью Р (АВ ⊥ Р) и найти совмещенное с основной плоскостью проекции положение точки встречи (рис. 27).

Построение совмещенного положения точки встречи К₀ прямой АВ с плоскостью Р показано на рис. 27.

Чтобы не загромождать чертеж, прямая АВ взята параллельно горизонтальной плоскости проекции. Спроецируем АВ прямоугольно на перпендикулярную к ней плоскость Р. Затем совместим плоскость Р и принадлежащую ей точку К с плоскостью V.

Проекцией прямой АВ на плоскость Р (при принятом направлении проецирования) будет точка К. Для перепроецирования точки К на плоскость V проведем биссекторную плоскость S, делящую пополам угол между плоскостями Р и V. Находим проекцию k_s точки К на плоскость S, направление проектирования принимаем перпендикулярным Р. Для определения k_s необходимо продолжить горизонтальную проекцию ab до пересечения с S_h. Из точки k_s, восставляем в плоскости S перпендикуляр к S_h до пересечения его с проекцией проецирующего луча, проходящего через a'b', получаем искомую точку K₀. Прямая S_h, имеет следующие свойства:

а) плоскость S делит угол между плоскостями Р и V пополам, поэтому S_h будет биссектрисой угла между Р_h, и его новым положением P_h0;

34

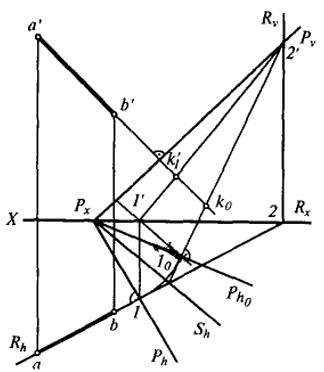
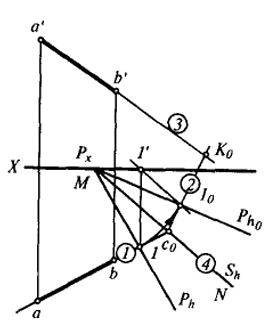
Рис. 28	Рис. 29

б) S_h является также горизонтальной проекцией прямой, по которой плоскость S пересекается с биссекторной плоскостью II и IV октантов, поэтому ее горизонтальная и фронтальная проекции совпадают.

Если через прямую АВ провести горизонтально проецирующую плоскость R, то она пересечет плоскость Р по прямой kk', которая будет являться геометрическим местом точек встречи всех прямых, лежащих в плоскости R с плоскостью Р.

Решим ту же задачу, но прямую АВ и плоскость Р возьмем общего положения, соблюдая лишь условие, чтобы АВ была перпендикулярна Р (рис. 28).

Проводим через АВ плоскость R, перпендикулярную Н. Строим линию пересечения плоскости R с плоскостью Р - 1 2.

На 1'2' находим фронтальную вспомогательную проекцию точки встречи k'₁ прямой с плоскостью. Переводим эту проекцию на плоскость V, пользуясь биссекторной плоскостью. Для этого определим совмещенное с плоскостью V положение Ph₀. Проводим S_h - биссектрису угла P_xP_hP_h0. Фронтальная проекция 2' точки 2 прямой 1 2, как лежащая на оси вращения Р_v, при вращении останется на месте. Для нахождения совмещенного положения точки 1₀ проектируем точку вначале на S_h, а затем на совмещенное с плоскостью V положение прямой 1 2. Тогда k'₁ при совмещении с плоскостью V будет перемещаться по направлению а'b', перпендикулярному оси вращения P_v, и определится в месте пересечения прямой а'b' с совмещенным положением 1₀2', т.е. в точке К₀. Точка K₀ является искомой прямоугольной проекцией прямой АВ на плоскость Р в совмещенном с плоскостью V положении.

35

Проследим, как можно сократить количество построений, выполненных на рис. 28.

Прямая ab перпендикулярна Р_h, следовательно, в совмещенном положении линия 1₀2' должна быть перпендикулярна P_h0. Поэтому для проведения прямой 1₀2' отпадает необходимость в построении точки 2', достаточно найти только точку 1₀ и определить направление совмещенного следа P_h0.

Следовательно, можно не проводить фронтальных следов Р_v и R_v, которые нужны для определения точки 2'. Точка 1₀ может быть построена с помощью точки 1' и направления фронтальной проекции прямой а'b' (так как a'b' ⊥ P_v). Тогда, отбросив лишние построения, рис. 28 можно представить в виде, изображенном на рис. 29. Полученный чертеж является схемой прямоугольного вспомогательного проецирования.

Из схемы видно, что задачу на построение изображения вспомогательной проекции в совмещенном положении выполнит дважды ломаная линия ас₀; c₀k₀; k₀a'. Участок ломаной линии ас₀ называется первым звеном, участок c₀k₀ - вторым звеном или носителем изображения, участок k₀a' - третьим звеном.

Прямая MN, совпадающая с S_h, называется осью вспомогательных построений. На этой прямой пересекаются все носители точек и горизонтальные проекции проецирующих лучей.

Из схемы (рис. 29) видно, что первое и третье звенья совпадают с соответственными направлениями горизонтальной и фронтальной проекции проектирующего луча (прямой АВ). Второе звено - носитель изображения - проходит через точку пересечения первого звена с осью MN перпендикулярно Р_h0. Ось вспомогательного проецирования совпадает с S_h, поэтому ее построение сводится к проведению биссектрисы угла между P_h и P_h0.

Для определения положения оси вспомогательного проецирования MN направления носителя изображения С.М. Колотов предлагает пользоваться специальной диаграммой, которую можно строить в стороне от чертежа.

Построение диаграммы сводится к следующему:

• 1) через произвольную точку М проводим прямую МО параллельно X (рис. 30);
• 2) из точки М проводим прямую M1, перпендикулярную горизонтальной проекции направления прямоугольного проецирования (расстояние M1 берется произвольным);
• 3) через точку 1 проводим прямую 1 1', перпендикулярную МО;

36

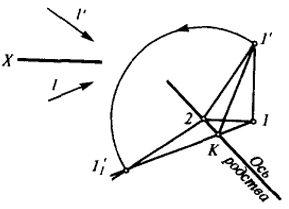
Рис. 30	Рис. 31

• 4) через 1' проводим прямую 1'1₀, параллельную фронтальной проекции направления прямоугольного проектирования;
• 5) радиусом M1 из точки М1₀ засекаем на прямой 1'1₀ точку 1₀;
• 6) через точку 1₀ проводим прямую, перпендикулярную М1₀, и продолжаем ее до пересечения с горизонтальной проекций проектирующего луча, проведенного через точку 1. Через точку пересечения проводим ось MN¹.

Легко убедиться, что диаграмма объединяет два действия, производимые над исследуемой точкой, а именно: проецирование ее на плоскость, перпендикулярную данному направлению, и приведение полученного изображения в совмещенное с фронтальной плоскостью проекций положение.

Пользуясь диаграммой, можно все построения на эпюре свести к механическому проведению линий параллельно звеньям диаграммы. А именно, если необходимо построить на эпюре вспомогательные проекции (в совмещенном положении) ряда точек, поступают следующим образом.

Через горизонтальные проекции точек проводят прямые, параллельные первому звену диаграммы. Проведенные прямые пересекают прямой, параллельной оси диаграммы.

Через полученные точки проводят прямые, параллельные второму звену диаграммы. Искомое положение точек определится пересечением этих прямых с прямыми, проведенными через фронтальные проекции точек параллельно третьему звену диаграммы.

Иной способ построения диаграмм предлагает Д.Н. Борисов. Не вдаваясь в подробности теоретических предпосылок способа зеркальных преобразований, покажем лишь построение диаграммы, которую Д.Н. Борисов называет проективной схемой. Ход построения следующий:

37

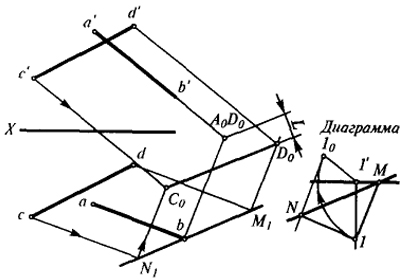
Рис. 32

• 1) строим прямоугольный треугольник 1'1 2 (рис. 31), гипотенуза которого 1'2 проводится перпендикулярно фронтальной проекции направления проецирования (l'); один из катетов этого треугольника 1 2 будет параллелен оси X, другой перпендикулярен ей;
• 2) через вершину 1 проводим прямую, параллельную горизонтальной проекции направления проецирования (l); из точки 2, как из центра, проводим дугу радиусом 2 1' до пересечения ее с проведенной прямой в точке 1'₁;
• 3) делим угол 1'₁ 2 1' пополам. Биссектриса этого угла дает направление оси родства (соответствующей оси MN в диаграмме С.М. Колотова);
• 4) направление второго звена (носителя изображения) определится прямой kl'.

Задача 1. Определить расстояние между скрещивающимися прямыми АВ и CD (рис. 32). Чтобы определить расстояние между скрещивающимися прямыми, нужно иметь проекцию, на которой одна из прямых проецировалась бы в точку. Очевидно, для получения такого вида проекций необходимо выбрать вспомогательную плоскость Р перпендикулярно прямой АВ (или CD) и спроецировать на эту плоскость прямую АВ (CD) в ее собственном направлении.

Для решения задачи воспользуемся диаграммой Колотова, которую построим в свободном месте чертежа (рис. 32).

Дальнейшие построения проводим в указанном выше порядке.

Искомое расстояние L определяется величиной перпендикуляра, опущенного из А₀В₀ на С₀D₀).

Задача 2. Определить угол между плоскостями Q(DB × АВ) S(DB × CB) (рис. 33).

38

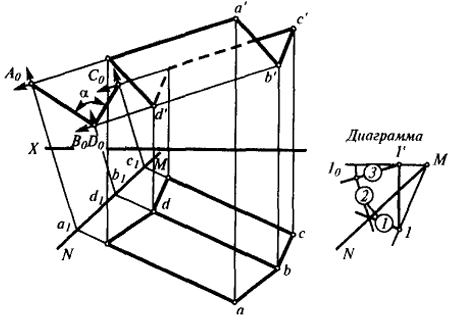
Рис. 33

Для нахождения действительной величины угла нужно спроецировать плоскости Q и S прямоугольно на третью плоскость Р, перпендикулярную им.

Это можно выполнить, если за направление проецирования принять прямую BD, по которой пересекаются плоскости Q и S, а плоскость Р взять перпендикулярной BD.

Выбрав направление проецирования, легко построить диаграмму (рис. 33). После этого для получения ответа на поставленную задачу необходимо через точки abc, а'b'с' и a₁b₁c₁ провести прямые, параллельные соответствующим звеньям диаграммы.

Точки А₀В₀С₀ определяют прямые А₀В₀ и В₀С₀, угол между которыми, спроецированный здесь в натуральную величину, и будет искомым углом α.

Косоугольное вспомогательное проецирование. При решении позиционных задач проф. С.М. Колотое предлагает пользоваться косоугольным проецированием на вспомогательную плоскость. Так как при решении таких задач не нужно определять истинные размеры проекций, то отпадает необходимость в построениях для получения их совмещенного положения; кроме того, оказывается возможным ограничиться построением только одной из проекций (фронтальной).

Косоугольное проецирование не дает действительных размеров изображаемых предметов, но сохраняет пропорциональную зависимость в расположении между изображениями отдельных геометрических элементов, составляющих проецируемый предмет. Это свойство не зависит от положения вспомогательной плоскости проекции.

39

Рис. 34

Применяя диаграмму Колотова для косоугольного проецирования, ее построения можно значительно упростить, выбирая в качестве новой плоскости проекции любую плоскость.

Так как на диаграмме ось вспомогательного проецирования MN и направление носителя изображения определяются положением вспомогательной плоскости, которая при косоугольном вспомогательном проецировании может выбираться произвольно, то можно задавать произвольно направления оси MN и носителя изображения.

Задача 1. Найти точку встречи прямой АВ с плоскостью Р (рис. 34).

Спроецируем плоскость Р и прямую АВ на произвольную горизонтально-проецирующую плоскость в направлении горизонтали плоскости Р. Диаграмма, соответствующая выбранному направлению проецирования и плоскости проекции, строится следующим образом.

Проводим произвольную прямую MN. Первое звено будет параллельно горизонтальной проекции горизонтали, второе звено - перпендикулярно оси X, третье звено - параллельно оси X (параллельно фронтальной проекции горизонтали).

Далее через точки а, b, 1, 2, 3 и а', b' проводим прямые, параллельные соответственно первому, второму и третьему звеньям диаграммы. Пересечение а'₁b'₁ (вспомогательной фронтальной проекцией прямой) с P_v1 определит k'₁. По k'₁ с помощью обратного луча находим k', a затем и k.

Задача 2. Определить точки встречи прямой АВ с трехгранной призмой 1, 2, 3 (рис. 35).

Задача определения точки встречи прямой с поверхностью призмы решается непосредственно на проекции, которая получается при параллельном проецировании на произвольную плоскость, если направление проецирования параллельно ребрам призмы. Поэтому при построении диаграммы следует иметь в виду, что первое и третье звенья

40

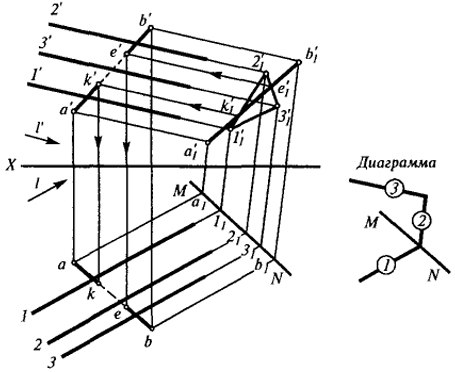
Рис. 35

параллельны соответственно горизонтальной l и фронтальной l' проекции проецирующего луча.

Второе звено и ось MN назначаются произвольно¹. Через горизонтальные проекции 1, 2, 3, а также а и b проводим прямые, параллельные первому звену до пересечения их с осью МN точках 1₁, 2₁, 3₁, а₁ и b₁. Через полученные точки проводим прямые, параллельные второму, а через фронтальные проекции 1', 2', 3', а', b' - прямые, параллельные третьему звену диаграммы.

Пересечение соответствующих прямых определит вспомогательные фронтальные проекции призмы и прямой 1'₁, 2'₁, 3'₁ и а'₁, b'₁.

Точки k'₁ и е'₁, в которых проекция прямой а'₁, b'₁ пересекает проекцию граней 2'₁3'₁ и 2'₁2'₁, будут вспомогательными проекциями искомых точек. Обратным построением находим их ортогональные проекции k', k и e', е.

Задача 3. Построить сечение пятигранной призмы, произвольно расположенной в пространстве плоскостью общего положения Р (рис. 36).

Спроецируем призму и плоскость Р на произвольную горизонтально проецирующую плоскость. За направление проецирования примем горизонталь плоскости Р. Строим диаграмму, отвечающую принятым условиям проецирования. Находим вспомогательные фронтальные

41

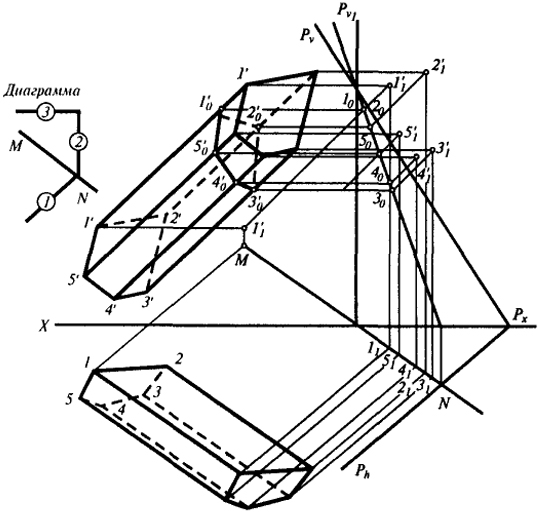
Рис. 36

проекции следа P_v (P_v1) и ребра призмы 1 1 (1'₁1'₁). Для определения вспомогательных фронтальных проекций остальных ребер достаточно построить точки 2'₁3'₁4'₁5'₁, через которые провести прямые, параллельные 1'₁1'₁. Затем из точек пересечения этих прямых 1₀, 2₀, 3₀, 4₀, 5₀ с новой фронтальной проекцией плоскости Р проводим прямые, параллельные третьему звену диаграммы до пересечения с фронтальными проекциями ребер призмы. Пятиугольник 1'₀2'₀3'₀4'₀5'₀ будет фронтальной проекцией искомого сечения.

Центральное вспомогательное проецирование. При решении позиционных задач, в которых участвуют пирамиды или конусы, целесообразно в качестве вспомогательного проецирования применять центральное проецирование, так как оно дает возможность наилучшим способом использовать закон образования поверхностей, ограничивающих упомянутые геометрические образы.

Ввиду того, что центральное проецирование так же, как и косоугольное вспомогательное проецирование, применяется для решения задач не метрического характера, то вспомогательная плоскость проекции и центр проецирования могут выбираться произвольно.

42

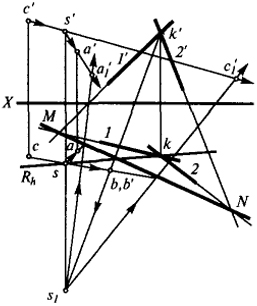
Рис. 37

При построении диаграммы центрального проецирования следует иметь в виду, что вторые звенья диаграммы (носители) для точек проецируемого объекта составляют пучок прямых, причем точка пересечения этих прямых не может быть назначена произвольно. Для ее построения надо провести вначале ось MN, которая, как было указано раньше, является проекцией линии пересечения вспомогательной плоскости проекции с биссекторной плоскостью второго и четвертого октантов. Поэтому ее построение сводится к определению двух точек, принадлежащих вспомогательной плоскости и удаленных от основных координатных плоскостей на равные расстояния.

Допустим, что задан центр проецирования S и плоскость проекций, определяемая пересекающимися прямыми 1 и 2 (рис. 37). В данном случае положение оси MN может быть найдено, если мы продолжим разноименные проекции прямых 1 и 2 до их взаимного пересечения.

Точка схода носителей может быть найдена, пользуясь точкой К. Через точки k и s проводим горизонтально-проецирующую плоскость R, которая пересечет вспомогательную плоскость по прямой ВК.

Фронтальная проекция b'k' и будет носителем. Пересечение носителя с прямой s's укажет фокус-точку схода носителей s₁.

Зная положение оси MN фокуса s₁, легко построить центральную вспомогательную проекцию любой точки пространства.

Для этого достаточно через горизонтальные проекции центра s и точки с провести горизонтальную проекцию луча (первое звено). Через точку пересечения первого звена с осью MN и фокус s₁ проводим второе звено до пересечения его с третьим звеном, проведенным через фронтальные проекции центра проецирования s' и точки с'.

На рис. 37 показано построение центральных проекций точек А и С.

Задача. Найти точки встречи прямой АВ с произвольной конической поверхностью (рис. 38).

Для решения этой задачи целесообразно за центр проекции принять вершину конуса S и спроецировать конус и прямую на плоскость основания конуса. Очевидно, при таком положении вспомогательной плоскости проекции и центра замкнутая кривая CDE будет являться

43

Рис. 38

центральной проекцией конуса. Чтобы построить центральную проекцию прямой АВ, нужно знать положение оси MN фокуса S₁. Для их определения воспользуемся прямыми 1 и 2, проходящими через точки СDЕ, лежащие в основании конуса, и точкой С.

Нахождение MN и S₁ выполнено по правилам, изложенным выше (см. рис. 37).

Для решения задачи достаточно построить только одну фронтальную проекцию а'₁b'₁.

Через точки k'₁ и l'₁, в которых а'₁b'₁ пересекает c'₁d'₁e'₁, проводим лучи s'k'₁ и s'l; пересечение их с прямой а'b' укажет фронтальные проекции искомых точек k' и l'.

44