§ 8. Сочетание способа перемены
плоскостей проекций со способом вращения

Пользуясь только одним способом вращения или только одним способом перемены плоскостей проекций, всегда можно перейти от произвольного положения какого-либо предмета к любому частному, обеспечивающему получение удобного вида проекций.

Однако иногда бывает целесообразно применять не один какой-либо способ, а использовать сочетание двух способов - перемену плоскостей проекций и вращения.

Существенным преимуществом способа перемены плоскостей проекции является построение только одной вспомогательной проекции (при замене одной плоскости проекции), в то время как способ вращения требует построения двух вспомогательных проекций (при повороте вокруг одной оси)¹. В то же самое время способ перемены плоскостей проекций обладает недостатком, заключающимся в том, что при замене плоскостей проекций трудно заранее точно предусмотреть на чертеже место расположения вспомогательных проекций. Применяя способ вращения, без указания положения осей (параллельное перемещение) всегда можно предусмотреть наиболее удобное положение вспомогательных проекций на поле чертежа.

Естественно возникает вопрос, каким путем возможно сочетать достоинства обоих способов: удобное расположение вспомогательных проекций (характерное для параллельного перемещения) и построение при каждом последовательном преобразовании только одной проекции (как в способе перемены плоскостей проекций).

Возможность совместного применения способов перемены плоскостей проекции и вращения была указана еще проф. В.И. Курдюмовым [17];

27

Рис. 23

сочетание этих способов известно под названием способа сложных перемещений.

Сложные перемещения могут быть подразделены на два вида.

Первый вид сложных перемещений состоит в том, что построение новых вспомогательных проекций достигается путем последовательного применения сперва способа перемены плоскостей проекции, затем вращения вокруг осей, перпендикулярной к новой плоскости.

Второй вид сложных перемещений заключается: а) в перемене плоскостей проекций с последующим совмещением новой плоскости с той из первоначальных плоскостей, которую она должна была заменить, или б) в перемене плоскостей проекций с последующим вращением, приводящим новую плоскость проекции в положение, параллельное той плоскости проекции, которую она заменила.

Ниже приведены решения задач на применение первого (задача 1) и второго (задача 2) видов сложных перемещений.

Задача 1. Точку А требуется повернуть против часовой стрелки вокруг фронтали MN на угол α (рис. 23).

Решение этой задачи способом вращения представляет определенные трудности, так как при вращении вокруг фронтали горизонтальная проекция окружности, по которой перемещается точка, имеет вид эллипса, и угол а будет проецироваться на горизонтальную плоскость с искажением. Решение можно значительно упростить, если применить способ сложных перемещений.

Построения, приведенные на рис. 23, выполнены в следующей последовательности. Проводим новую Х₁ перпендикулярно т'п', тогда новая горизонтальная проекция спроецируется в точку (центр вращения). Величина радиуса вращения определяется расстоянием новой горизонтальной проекции а₁ от центра вращения т₁п₁: Затем вращаем точку а₁ (при этом а₁ перемещается по дуге окружности), пока она не займет положение а₃, соответствующее повороту ее на заданный угол α. Обратным построением возвращаем точку а₃ на исходные плоскости проекций и находим a'₂ и а₂.

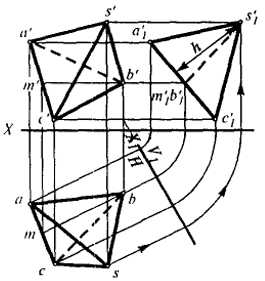
Задача 2. Определить высоту четырехгранной пирамиды SABC (рис. 24).

При решении этой задачи используем замену плоскости проекции V на V₁ с последующим совмещением ее с плоскостью V. Для определения направления новой оси X₁ в плоскости основания ABC проводим

28

Рис. 24	Рис. 25

горизонталь ВМ. Х₁ проведем перпендикулярно bт. Совмещаем новую плоскость V₁ с плоскостью V. В совмещенном положении плоскости строим совмещенную проекцию пирамиды s'₁a'₁b'₁c'₁. Величина перпендикуляра h, опущенного из s'₁ на а'₁с₁, определяем высоту пирамиды.

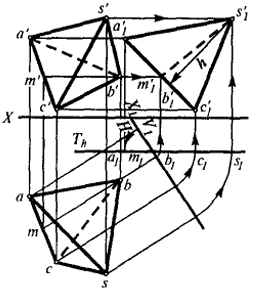
Эту задачу можно решить также и заменой плоскости V на V₁ с последующим вращением ее вокруг оси, перпендикулярной плоскости H до положения, параллельного плоскости V (вариант "б" второго вида сложных перемещений).

Необходимые построения выполнены на рис. 25 и дополнительных пояснений не требуют.

Из примеров, приведенных на рис. 24 и 25, видно, что для получения ответа с помощью сочетания двух способов потребовалось построить только одну вспомогательную проекцию.

Решая эту задачу способом вращения, пришлось бы строить две вспомогательные проекции.

Используя сочетание различных способов, можно существенно упростить решение целого ряда задач, особенно в тех случаях, когда необходимо повернуть плоскую или пространственную фигуру вокруг прямой общего положения.

Следует иметь в виду, что количество геометрических построений будет уменьшено только в том случае, если мы заменяем вращение переменной плоскостей проекций (а не наоборот).

В.Л. Торохов предложил способ замены плоскостей проекций V и H одновременно двумя взаимно перпендикулярными плоскостями.

Как известно, способ перемены плоскостей проекций позволяет лишь последовательно заменять плоскости проекций с обязательным соблюдением условия, чтобы вновь вводимая плоскость была перпендикулярна

29

заданной плоскости проекции или к предварительно замененной плоскости.

Иными словами, переход от заданной системы плоскостей проекции X к новой X₂ возможен только путем последовательной замены вначале V на V₁ (или H на Н₁) и лишь после этого Н на Н₁ (или V на V₁), т.е. по схеме

Х

V

H

 → Х₁

V1

H

 → Х₂

V1

H1

или

Х

V

H

 → Х₁

V

H1

 → Х₂

V1

H1

В.Л. Торохов предложил переход от заданной системы Х

V

H

 к новой X₂

V1

H1

 - осуществлять непосредственно, минуя промежуточное звено Х₁

V1

H

 (или Х₁

V

H1

).

Система заданных плоскостей проекции Х 

V

H

 заменяется новой системой взаимно перпендикулярных плоскостей R и Q, причем одна из этих плоскостей должна быть перпендикулярна какой-либо из заданных плоскостей проекций, допустим к H. Проецируем предмет на эти новые плоскости. Затем совмещаем плоскость R с плоскостью V (а не с H, как этого требует способ перемены плоскостей проекции). После того как построения, связанные с совмещением R с V, будут закончены, совмещаем плоскость Q с H.

Проследим применение изложенного способа на примере решения задачи по определению расстояния между скрещивающимися прямыми АВ и CD (рис. 26).

Заключаем прямую CD в горизонтально-проецирующую плоскость R. Из горизонтальных проекций а и b опускаем перпендикуляры на след R_H, которые пересекут его в точках а₁ и b₁. После совмещения R

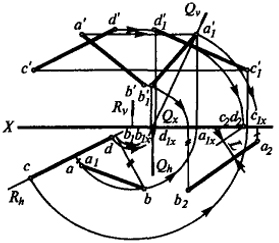
Рис. 26

30

с V точки b₁, d, a₁, c переместятся в точки b_1x, d_1x, а_1х, с_1х на оси X. Новые фронтальные проекции точек могут быть найдены в результате пересечения перпендикуляров к оси X, восставленных из точек b_1x, d_1x, а_1х, с_1х с прямыми, проведенными параллельно оси X через исходные фронтальные проекции точек. Соединив попарно точки а'₁b'₁ и c'₁d'₁, получим новые фронтальные проекции заданных прямых. Так как плоскости R и Q перпендикулярны, то фронтальный след плоскости Q_v займет направление, перпендикулярное c'₁d'₁.

Точку схода следов Q_x можно выбирать произвольно; для удобства дальнейших построений выбираем ее так, чтобы след Q_v прошел через точку а'₁. Затем проецируем новые фронтальные проекции точек b'₁, с'₁, d'₁ на след Q_v в точки (на рис. 26 эти точки не обозначены), которые после совмещения плоскости Q с Н займут положение b_2x, c_2x, d_2x, a_2x; ординаты точек а₂, c₂, b₂, d₂ должны соответствовать удалению точек а, с, bd от следа R_h. Расстояние между точкой c₂d₂ и отрезком a₂b₂ - искомые.

31