У спиральных канатов или прядей, загруженных растягивающей силой, в проволоках появляются напряжения, действительные величины которых определяются не только растяжением, но и изгибом, кручением, поперечным сжатием, вытяжкой, свивкой и другими факторами. Влияние перечисленных факторов на напряженное состояние различно и в отдельных случаях пренебрежимо мало, в целом напряжения в канатах определяются через силу S, действующую на канат, и численно равны:
19
σz =
(1.3)
Здесь Ad - поперечное сечение каната, равное сумме площадей проволочек диаметром di
Ad = · di2
(1.4)
На отдельную проволоку, расположенную в ряду i, действует часть внешней силы Si, направленной вдоль оси каната, а также соответствующая часть крутящей силы Ui, от крутящего момента. Внешние силы Si и Ui уравновешиваются внутренними, продольным Fi и поперечным Qi усилиями. На рис. 1.14 приведён многоугольник сил, действующих на проволоку.
 Рис. 1.14. Многоугольник сил, действующих на проволоку
Рис. 1.14. Многоугольник сил, действующих на проволоку
Из условия равновесия получим:
Fi =
(1.5)
Ui = Fi · Sin αi - Q · Cos αi
(1.6)
Здесь αi, - угол свивки каната. Значение поперечной силы Qi в уравнениях (1.5) и (1.6) не известно. Её величину можно определить из условий изгиба и кручения проволок. Значения Qi зависят от радиусов свивки ri.
Qi = (Mu · Cos αi - Mkp · Sin αi)
(1.7)
20
Величины изгибающих (Мu) и крутящих (Мкр) моментов при действии растягивающих сил очень малы, а следовательно, и величина поперечной силы также может быть пренебрежимо мала и уравнения (1.5), (1.6) будут иметь вид
Fi =
(1.8)
Для крутящей силы соответственно
Ui = Fi · Sin αi
(1.9)
или
Ui = Si · tg αi
(1.10)
Крутящий момент относительно оси каната или пряди в проволоках положения i
Mi = Fi · ri · Sin αi
(1.11)
Mi = Si · ri · tg αi
(1.12)
Представленные зависимости получены рядом авторов [73], [78]. Внешняя сила S, действующая на канат, будет равна сумме компонентов составляющих
S = Zi · Si = Zi · Fi · Cos αi
(1.13)
где п - число рядов проволок в канате или пряди, для сердечника i = 0;
Zi - число проволок в ряду.
Под действием растягивающей силы S канат на длине свивки lудлинится на величину Δl и величина усилия в проволоке Fi может быть выражена следующим образом
Fi = · Ei · Ai
(1.14)
Относительное удлинение проволоки
εi =
(1.15)
Длина проволоки
li =
(1.16)
На рис. 1.15 показано удлинение элемента каната длиной l под действием внешней нагрузки. Удлинение проволоки Δli
Δli = (Δl - ΔUi · tg α) · Cos αi
(1.17)
или
Δli = Δl · Cos αi - ΔUi · Sin αi
(1.18)
21
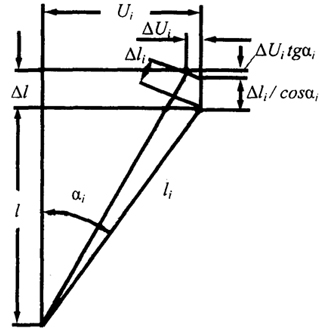 Рис. 1.15. Удлинение проволоки в пряди длиной l под действием внешней нагрузки
Рис. 1.15. Удлинение проволоки в пряди длиной l под действием внешней нагрузки
После преобразования выражений с учётом коэффициента поперечной деформации μ получим
Δli + Δli · μi · Sin2αi
(1.19)
Отсюда имеем
Δli = | Δl · Cos αi |
| 1 + μi · Sin2αi |
(1.20)
С учётом (1.13)и(1.15) растягивающее усилие в проволоке l равно
Fi = | Δl · Cos2αi |
| l(1 + μi · Sin2αi) |
· Ei · Ai
(1.21)
или
Si = | Δl · Cos3αi |
| l(1 + μi · Sin2αi) |
· Ei · Ai
(1.22)
Подставляя значения (1.21)в(1.13), получим
S = (| Zi · Cos3αi |
| 1 + μi · Sin2αi |
· Ei · Ai)
(1.23)
Усилие в отдельной проволоке пряди или однопрядного каната определяется по формуле
Fk = | · Ek · Ak |
(| Zi · Cos3αi | | 1 + μi · Sin2αi |
· Ei · Ai) |
· S
(1.24)
22
Как видно из формулы (1.23), величина усилия в проволоке зависит от её жёсткостных характеристик и угла свивки данного ряда. Например, для проволоки одинакового диаметра и угла свивки при фиксированных значениях отношения шага свивки к диаметру каната, равному 10 (k = l / D = 10), и соответствующем угле свивки α = 17.7° усилие в проволоке возрастает на 5% по сравнению с продольной силой, приходящейся на эту проволоку.
Относительная деформация каната
ε = | S |
(| Zi · Cos3αi | | 1 + μi · Sin2αi |
· Ei · Ai) |
(1.25)
Исходя из вышеизложенного, напряжения в различных рядах проволок каната различны, зависят от их положения и угла свивки и отличаются от величин, полученных по формуле (1.3). Согласно [44] расчётное усилие растяжения каната п в расчётах на прочность должно удовлетворять неравенству
≤ Ru
(1.26)
где Ru - расчётное сопротивление каната. Расчётное сопротивление каната определяется по формуле
Ru = · Run
(1.27)
- где γc - коэффициент общих условий работы канатного элемента;
- γk - коэффициент условий работы, учитывающий влияние на прочность каната местных концентраторов напряжений;
- γu = 1,3 - коэффициент надёжности для элементов конструкций, расчитываемых по временному сопротивлению разрыву;
- γm = 1.2 - коэффициент надёжности стальных канатов по материалу;
- γn - коэффициент надёжности по назначению, учитывающий степень ответственности и капитальности сооружения;
- Run - нормативное сопротивление каната, определяемое по его разрывному усилию или в соответствии с пунктом 3 [44].
Полученное расчетное сопротивление не принимать более 0.7 Run
Дополнительные напряжения, отмеченные ранее и возникающие в процессе загружения проволок статической нагрузкой, в расчёте не учитываются. Эти напряжения могут быть учтены при расчёте выносливости при загружении переменной нагрузкой.
23
