В предварительно напряженных и висячих конструкциях имеется часть элементов, работающих на сжатие, несущая способность которых определяется не из условия прочности, а из условия устойчивости. Проблема определения устойчивости конструкции и ее элементов также может быть успешно решена с помощью метода конечных элементов. Для сжатых стержней различают проблему разветвления форм равновесия при достижении нагрузкой критических значений и проблему устойчивости положения или потери устойчивости равновесия в большом, то есть "прощелкивание" системы после сообщения ей некоторой дополнительной энергии для преодоления энергетического барьера (рис. 3.22). Примером такой системы является ферма Мизеса.
207
При значениях Р (рис. 3.22), не превышающих Ркr, каждой величине нагрузки соответствует параметр перемещения d. Система устойчива и находится в равновесии. При достижении нагрузкой предельного критического значения наступает индифферентное граничное состояние.
Дальнейшее приращение перемещения приводит к изменению формы системы ("прощелкивание системы") при уменьшающейся нагрузке до тех пор, пока не будет достигнуто новое устойчивое состояние равновесия. Для реальных конструкций подобное поведение является динамическим процессом.
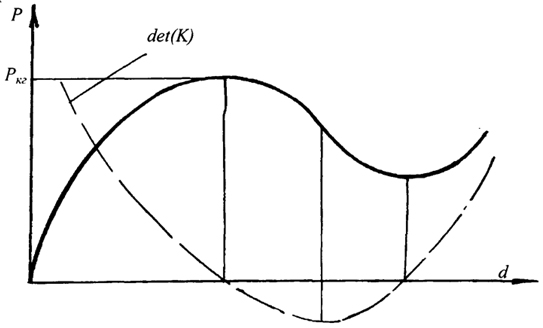Рис. 3.22. Диаграммы изменения перемещений и детерминанты при действии нагрузки
Аналогичным образом могут исследоваться проблемы закритической работы конструкции, а также расчета внецентренно сжатых элементов.
В реальных конструкциях вследствие наличия неизбежных дефектов проблема разветвления форм равновесия реализуется очень редко. Большинство задач разветвления форм равновесия путем ввода малой возмущающей нагрузки могут быть сведены задаче изучения закритической работы или исследованию внецентренно сжатых элементов.
При расчете нелинейных систем методом Ньютона-Рафсона затруднительно определить закритическую ветвь поведения конструкций под нагрузкой. Такой расчет может быть реализован методом корректировки энергии деформации изложенным выше.
Рис. 3.23 иллюстрирует принцип определения перемещения конструкции под нагрузкой в закритической стадии с помощью корректировки энергии деформации.
208
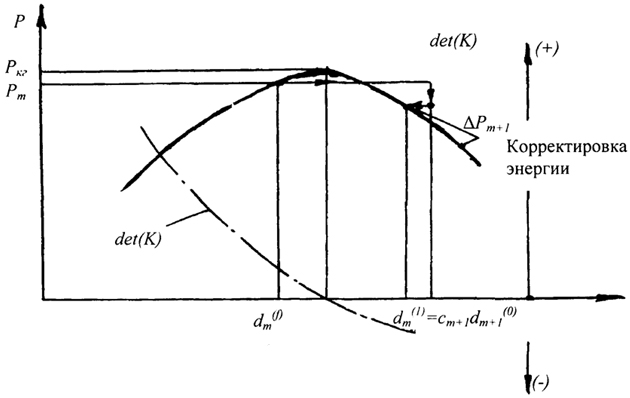Рис. 3.23. Принцип определения перемещения конструкции под нагрузкой
Однородная система уравнений
(K(0)+K(1)+K(2)) · Δd = 0 .
(3.83)
только тогда имеет нетривиальное решение, когда детерминанта тангенциальной матрицы жесткости (det К), являющейся составной частью алгоритма расчета, равна нулю. При detK > 0 система устойчива; при detK = 0 - индифферентное состояние; при detK < 0 - состояние неустойчивого равновесия.
209
